Panel data refer to data sets consisting of multiple observations on each sampling unit. This could be generated by pooling time series observations across a variety of cross-sectional units, including countries, hospitals, firms, or randomly sampled individuals, like nurses, doctors, and patients. This encompasses longitudinal data analysis in which the primary focus is on individual histories. Two well-known examples of the US panel data are the Panel Study of Income Dynamics, and the National Longitudinal Surveys of Labor Market Experience. European panels include the German Socioeconomic Panel, the British Household Panel Survey (BHPS), and the European Community Household Panel (ECHP). Panel data methods in health economics have been used to estimate the labor supply of physicians and nurses; study the relationship between health and wages and health and economic growth; examine the productivity and cost efficiency of hospitals; and estimate the effect of pollutants on mortality. They have also been used to study the relationship between obesity and fast food prices; determine whether beer taxes will reduce motor vehicle fatality rates; and whether cigarette taxes will reduce teenage smoking, to mention a few applications. For example, Askildsen et al., 2003 estimate nurse’s labor supply for Norway. The panel data used include detailed information on 19 638 nurses observed over the period 1993–98. The policy question tackled is whether increasing wages would entice nurses to supply more hours of work. Contoyannis and Rice, 2001 estimate the impact of health on wage rates using the first six waves of the BHPS. Abrevaya (2006) utilizes the federal Natality Data Sets (released by the National Center for Health Statistics) from 1990 to 1998, to estimate the causal effect of smoking on birth outcomes. Identification of the smoking effect is achieved in this panel from women who change their smoking behavior from one pregnancy to another. Abrevaya constructs a matched panel data set that identifies mothers with multiple births. With the most stringent matched criterion, this data set contains 296 218 birth observations with 141 929 distinct mothers. Baltagi and Geishecker (2006) estimate a rational addiction model for alcohol consumption in Russia. Their panel data set includes eight rounds of the Russian Longitudinal Monitoring Survey spanning the period 1994–2003. These are four examples of micropanel data applications in health economics and as clear from these data sets, they follow a large number of individuals over a short period of time.
In contrast, examples of macropanels in health economics include Ruhm (1996) who uses panel data of 48 states (excluding Alaska, Hawaii, and the District of Columbia) over the period 1982–88 to study the impact of beer taxes and a variety of alcohol-control policies on motor vehicle fatality rates. Greene (2010) who uses the World Health Organization’s panel data set to distinguish between cross-country heterogeneity and inefficiency in health-care delivery. This panel follows 191 countries over the period 1993–97. Becker, Grossman, and Murphy (1994), who estimate a rational addiction model for cigarette consumption across 50 states (and the District of Columbia) over the period 1955–85. Baltagi and Moscone (2010) who use a panel of 20 Organization for Economic Co-operation and Development countries observed over the period 1971–2004 to estimate the long-run economic relationship between health-care expenditure and income. Macropanels follow aggregates like countries, states, or regions and usually involve a longer period of time than micropanels. The asymptotics for micropanels has to be for large N, as T is fixed and usually small, whereas the asymptotics for macropanels can be for large N and T. Also, with a longer time series for macropanels one has to deal with issues of nonstationarity in the time series, like unit roots, structural breaks, and cointegration (see Chapter 12 of Baltagi, 2008). Additionally, with macropanels, one has to deal with cross-country dependence. This is usually not an issue in micropanels where the households are randomly sampled and hence not likely correlated.
Some of the benefits of using panel data include a much larger data set. This means that there will be more variability and less collinearity among the variables than is typical of cross-sectional or time series data. With additional, more informative data, one can get more reliable estimates and test more sophisticated behavioral models with less restrictive assumptions. Another advantage of panel data is their ability to control for individual heterogeneity. Not controlling for these unobserved individual-specific effects leads to bias in the resulting estimates. For example, consider the Abrevaya (2006) application, where one is estimating the causal effect of smoking on birth weight. One would expect that mothers who smoke during pregnancy are more likely to adopt other unhealthy behavior such as drinking, poor nutritional intake, etc. These variables are unobserved and hence omitted from the regression. If these omitted variables are positively correlated with the mother’s decision to smoke, then ordinary least squares (OLS) will result in an overestimation of the effect of smoking on birth weight. Similarly, in the Contoyannis and Rice (2001) study, where one is estimating the effect of health status on earnings, one would expect the health status of the individual to be correlated with unobservable attributes of that individual, which, in turn, affect productivity and wages. If this correlation is positive, one would expect an overestimation of the effect of health status on wages. Cross-sectional studies attempt to control for this unobserved ability by collecting hard-to-get data on twins. However, using individual panel data, one can, for example, difference the data over time and wipe out the unobserved individual invariant ability.
Another advantage of panels over cross-sectional data is that individuals ‘anchor’ their scale at different levels, rendering interpersonal comparisons of responses meaningless. When you ask people about their health status on a scale of 1–10, Sam’s 5 may be different from Monica’s 5, but in a cross-sectional regression you assume they are the same. Panel data help if the metric used by individuals is time-invariant. Fixed effects (FE) makes inference based on intrarather than interpersonal comparisons of satisfaction. This avoids not only the potential bias caused by anchoring but also bias caused by other unobserved individual-specific factors.
Limitations of panel data sets include problems in the design, data collection, and data management of panel surveys. These include the problems of coverage (incomplete account of the population of interest), nonresponse (due to lack of cooperation of the respondent or because of interviewer error), recall (respondent not remembering correctly), frequency of interviewing, interview spacing, reference period, the use of bounding to prevent the shifting of events from outside the recall period into the recall period, and time-in-sample bias. Another limitation of panel data sets is the distortion due to measurement errors. Measurement errors may arise because of faulty response due to unclear questions, memory errors, deliberate distortion of responses (e.g., prestige bias), inappropriate informants, misrecording of responses, and interviewer effects. Although these problems can occur in cross-sectional studies, they are aggravated in panel data studies. Panel data sets may also exhibit bias due to sample selection problems. For the initial wave of the panel, respondents may refuse to participate or the interviewer may not find anybody at home. This may cause some bias in the inference drawn from this sample. Although this nonresponse can also occur in cross-sectional data sets, it is more serious with panels because subsequent waves of the panel are still subject to nonresponse. Respondents may die, move, or find that the cost of responding is high.
The Model
Most panel data applications use a simple regression with error component disturbances:
![]()
with i denoting individuals, hospitals, countries, etc. and t denoting time. The i subscript, therefore, denotes the cross-sectional dimension, whereas t denotes the time series dimension. The panel data are balanced in that none of the observations are missing whether randomly or nonrandomly due to attrition or sample selection. a is a scalar, β is K×1, and Xit is the it-th observation on K explanatory variables. μi denotes the unobservable individual-specific effect and vit denotes the remainder disturbances, which are assumed to be independent and identically distributed IID (0;σ2v) . For example, in the Contoyannis and Rice (2001) study of the impact of health on wage rates using the first six waves of the BHPS, yit is log of average hourly wage, whereas Xit contains a set of variables like age, age2, experience, experience2, union membership, marital status, number of children, race, education, occupation, region indicator, etc. The variable of interest is a self-assessed health variable, which is obtained from the response to the following question: ‘‘Please think back over the last 12 months about how your health has been. Compared to people of your own age, would you say that your health has on the whole been excellent/good/fair/poor/very poor?’’ Contoyannis and Rice constructed three dummy variables: (sahex=1, if an individual has excellent health), (sahgd =1, if an individual has good health), and (sahfp =1, if an individual has fair health or worse). They also included a General Health Questionnaire: Likert Scale score which was originally developed as a screening instrument for psychiatric illness but is often used as an indicator of subjective wellbeing. Contoyannis and Rice constructed a composite measure derived from the results of this questionnaire which is increasing in ill health (hlghq1).
Fixed Effects
Note that μi is time invariant and it accounts for any individual-specific effect that is not included in the regression. If the μi`s are assumed as fixed parameters to be estimated and the X`its are assumed independent of the vit for all i and t, the FE model is obtained. Estimation in this case amounts to including (N-1) individual dummies to estimate these individual invariant effects. This leads to an enormous loss in degrees of freedom and attenuates the problem of multicollinearity among the regressors. Furthermore, this may not be computationally feasible for large micropanels. By the Frisch–Waugh–Lovell Theorem (Baltagi, 2008) one can get this FE estimator by running least squares of yit=yit -yi on the Xit ’s similarly defined, where the dot indicates summation over that index and the bar denotes averaging. This transformation eliminates the μ’is and is known as the within transformation and the corresponding estimator of β is called the within estimator or the FE estimator. Note that the FE estimator cannot estimate the effect of any time-invariant variable, such as race or education. These variables are wiped out by the within transformation. This is a major disadvantage if the effect of these variables on earnings is of interest. Note that, if T is fixed and N→∞ as typical in short labor panels, then only the FE estimator of β is consistent; the FE estimators of the individual effects (a+ μi) are not consistent because the number of these parameters increases as N increases. This is known as the incidental parameter problem. Note that when the true model is FE, OLS suffers from omission variables bias and inference using OLS is misleading. For the sample of 859 males in the Contoyannis and Rice (2001) study, the OLS estimate for excellent health is 0.065 and significant, whereas the OLS estimate for good health is 0.019 and insignificant (both are contrasted against a baseline of fair, poor, and very poor health). The FE estimates are 0.013 for excellent health and 0.010 for good health, and both are insignificant. The OLS estimate for the General Health Questionnaire: Likert Scale score (hlghq1) is 0.002 and insignificant, whereas the FE estimate is 0.003 and significant. More dramatically, for the Ruhm (1996) study, OLS gets a positive (0.012) and significant effect of real beer taxes on motor vehicle fatality rates, whereas FE obtains a negative (-0.324) and significant effect of real beer taxes on motor vehicle fatality rates.
Janke et al. (2009) examine the relationship between population mortality and common sources of airborne pollution in England. The data covers 312 local authorities over the period 1998–2005. They find that higher levels of PM10 (particulate matter less than 10 mm in diameter) and ozone (O3) have a positive and significant effect on mortality rates. The OLS estimate for (PM10/10), controlling for three other measures of pollutants (carbon monoxide, nitrogen dioxide, and O3), smoking rate, employment rate, etc. is 2.33, whereas that for FE is 2.74. The OLS estimate for (O3/10) in the same regression is 0.55, whereas that for FE is 0.80. Only the FE estimates for these pollutants are significant at the 5% level.
One could test the joint significance of the individual effects, i.e., H0;μ1= μ2=…=μN-1 =0, by performing an F-test. This is a simple Chow test with the restricted residual sums of squares being that of OLS on the pooled model and the unrestricted residual sums of squares (URSS) being that which includes the (N-1) individual dummies. By the Frisch–Waugh–Lovell theorem (Baltagi, 2008), URSS can be obtained from the within regression residual sum of squares. In this case
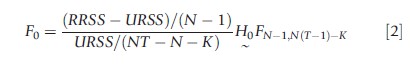
For the Contoyannis and Rice (2001) application, This Fstatistic is 12.50 and is distributed under the null hypothesis as F(858, 3406). This is significant and rejects H0. One can infer that the OLS estimates are biased and inconsistent and yield misleading inference.
Difference-In-Differences
Note that the FE transformation (yit =yit -yi) is not the only transformation that will wipe out the individual effects. In fact, FD will also do the trick (∆yi=yit -yi,t-1). This is a crucial tool used in the difference-in-differences (DID) estimator. Before the approval of any drug, it is necessary to assign patients randomly to receive the drug or a placebo and the drug is approved or disapproved depending on the difference in the health outcome between these two groups. In this case, the FDA is concerned with the drug’s safety and its effectiveness. However, one runs into problems in setting this experiment. How can one hold other factors constant? Even twins which have been used in economic studies are not identical and may have different life experiences. With panel data, observations on the same subjects before and after a health policy change allow us to estimate the effectiveness of this policy on the treated and control groups without the contamination of individual effects. In simple regression form, assuming the assignment to the control and treatment groups is random, one regresses the change in the health outcome before and after the health policy is enacted on a dummy variable which takes the value 1 if the individual is in the affected (treatment) group and 0 if the individual is in the unaffected (control) group. This regression computes the average change in the health outcome for the treatment group before and after the policy change and subtracts that from the average change in the health outcome for the control group. One can include additional regressors which measure the individual characteristics before the policy change. Examples are gender, race, education, and age of the individual. This is known as the DID estimator in econometrics. Alternatively, one can regress the health outcome y on dg dt and their interaction dt ×dg. dg is a dummy variable that takes the value 1 if the subject is in the treatment group, and 0 otherwise; dt is a dummy variable which takes the value 1 for the posttreatment period, and 0 otherwise. In this case, dt ×dg takes the value 1 only for observations in the treatment group and in the post-treatment period. The OLS estimate of the coefficient of dt ×dg yields the DID estimator. Another advantage of running this regression is that one can robustify the standard errors with standard software.
In economics, one cannot conduct medical experiments. Card (1990) used a natural experiment to see whether immigration reduces wages. Taking advantage of the ‘Mariel boatlift’ where a large number of Cuban immigrants entered Miami, Card (1990) compared the change in wages of low skilled workers in Miami with the change in wages of similar workers in other comparable US cities over the same period. Card concluded that the influx of Cuban immigrants had a negligible effect on wages of less-skilled workers. Gruber and Poterba (1994) use the DID estimator to show that a change in the tax law did increase the purchase of health insurance among the self-employed. They compared the fraction of the self-employed who had health insurance before the tax change 1985–86 with the period after the tax change 1988–89. The control group was the fraction of employed (not self-employed) workers with health insurance in those years.
Donald and Lang (2007) warn that the standard asymptotics for the DID estimator cannot be applied when the number of groups is small, as in the case where one compares two states in 2 years or self-employed workers and employees over a small number of years. They reconsider the Gruber and Poterba (1994) paper on health insurance and self-employment and Card’s (1990) study of the Mariel boatlift. They show that analyzing the t-statistic, taking into account a possible group error component, dramatically reduces the precision of their results. In fact for Card’s (1990) Mariel boatlift study, their findings suggest that the data cannot exclude large effects of the migration on blacks in Miami.
Bertrand et al. (2004) argued that several DID studies in economics rely on a long time series. They warn that in this case, serial correlation will understate the standard error of the estimated treatment effects, leading to overestimation of t-statistics and significance levels. They show that the block bootstrap (taking into account the autocorrelation of the data) works well when the number of states is large enough. Readers are advised to refer to Hansen (2007) for inference in panel models with serial correlation and FE and to Stock and Watson (2008) for a heteroskedasticity-robust variance matrix estimator for the FE estimator. Hausman and Kuersteiner (2008) warn that both the DID and the FE estimators are not efficient if the stochastic disturbances are serially correlated. The optimal estimator in this case is generalized least squares (GLS), but this is rarely used in applications of DID studies. Hausman and Kuersteiner (2008) use higher order Edgeworth expansion to construct a size-corrected t-statistic (based on feasible GLS) for the significance of treatment variables in DID regressions. They find that size-corrected t-statistic based on feasible GLS yields accurate size and is significantly more powerful than robust OLS when serial correlation in the level data is high.
Conley and Taber (2011) consider the case where there are only a small number N1 of treatment groups, say states, that change a law or policy within a fixed time span T. Let N0 denote the number of control groups (states) that do not change their policy. Conley and Taber argue that the standard large-sample approximations used for inference can be misleading especially in the case of non-Gaussian or serially correlated errors. They suggest an alternative approach to inference under the assumption that N1 is finite, using asymptotic approximations that let N0 grow large, with T fixed. Point estimators of the treatment effect parameter(s) are not consistent as N1 and T are fixed. However, they use information from the N0 control groups to consistently estimate the distribution of these point estimators up to the true values of the parameter.
DID estimation has its benefits and limitations. It is simple to compute and it controls for heterogeneity of the individuals or the groups considered before and after the policy change. However, it does not account for the possible endogeneity of the interventions themselves (Besley and Case, 2000). Abadie (2005) discusses how well the comparison groups used in nonexperimental studies approximate appropriate control groups. Athey and Imbens (2006) critique the linearity assumptions used in DID estimation and provide a general changes-in-changes (CIC) estimator that does not require such assumptions.
The DID estimator requires that, in the absence of the treatment, the average outcomes for the treated and control groups would have followed parallel paths over time. This assumption may be too restrictive. Abadie (2005) considers the case in which differences in observed characteristics create nonparallel outcome dynamics between treated and controls. He proposes a family of semiparametric DID estimators which can be used to estimate the average effect of the treatment for the treated. Abadie et al. (2010) advocate the use of data-driven procedures to construct suitable comparison groups. Datadriven procedures reduce discretion in the choice of the comparison control units, forcing researchers to demonstrate the affinities between the affected and unaffected units using observed quantifiable characteristics. The idea behind the synthetic control approach is that a combination of units often provides a better comparison for the unit exposed to the intervention than any single unit alone. They apply the synthetic control method to study the effects of California’s Proposition 99, a large-scale tobacco control program implemented in California in 1988. They demonstrate that following the passage of Proposition 99, tobacco consumption fell markedly in California relative to a comparable synthetic control region. They estimated that by the year 2000, annual per capita cigarette sales in California were approximately 26 packs lower than what they would have been in the absence of Proposition 99.
Athey and Imbens (2006) generalize the DID methodology to what they call the CIC methodology. Their approach allow the effects of both time and the treatment to differ systematically across individuals, as when new medical technology differentially benefits sicker patients. They propose an estimator for the entire counterfactual distribution of effects of the treatment on the treatment group as well as the distribution of effects of the treatment on the control group, where the two distributions may differ from each other in arbitrary ways. They provide conditions under which the proposed model is identified nonparametrically and extend the model to allow for discrete outcomes. They also provide extensions to settings with multiple groups and multiple time periods. They revisit the Meyer et al. (1995) study on the effects of disability insurance on injury durations. They show that the CIC approach leads to results that differ from the standard DID results in terms of magnitude and significance. They attribute this to the restrictive assumptions required for the standard DID methods.
Laporte and Windmeijer (2005) show that the FE and FD estimators lead to very different estimates of treatment effects when these are not constant over time, and treatment is a state that only changes occasionally. They suggest allowing for flexible time-varying treatment effects when estimating panel data models with binary indicator variables. They illustrate this by looking at the effect of divorce on mental well-being using the BHPS. They show that divorce has an adverse effect on mental well-being that starts before the actual divorce, peaks in the year of the divorce, and diminishes rapidly thereafter. A model that implies a constant instantaneous effect of divorce leads to very different FD and FE estimates, whereas a model that allows for flexibility in these effects lead to similar results. In general, the FE estimator is more efficient than the FD estimator when the remainder disturbance vit~IID(0,σ2v). The FD estimator is more efficient than the FE estimator when the remainder disturbance vit is a random walk (Wooldridge, 2002). These estimators are affected differently by measurement error and by nonstationarity (Baltagi, 2008).
Certainly, this analysis can be refined to account for perhaps better control and treatment groups. If a policy is enacted by state s to reduce teenage smoking or motor vehicle fatality due to alcohol consumption or healthcare service for the elderly, then, for the two periods case, dt takes the value 1 for the postpolicy period, and 0 otherwise; ds takes the value 1 if the state has implemented this policy, and 0 otherwise; and dg takes the value 1 for the treatment group affected by this policy like the elderly, and 0 otherwise. In this case, one regresses health-care outcome on dt,ds,dg, dt ×dg,dt × ds,ds× dg and dt × ds×dg. The OLS estimate of the coefficient of dt× ds× dg yields the difference-in-difference-in-differences estimator of this policy. This estimator computes the average change in the health outcome for the elderly in the treatment state before and after the policy is implemented, and then subtracts from that the average change in the health outcome for the elderly in the control state, as well as the average change in the health outcome for the nonelderly in the treatment state.
Carpenter (2004) studied the effect of zero-tolerance (ZT) driving laws on alcohol-related behaviors of 18–20-year olds, controlling for macroeconomic conditions, other alcohol policies, state FE, survey year and month effects, and linear state-specific time trends. ZT Laws make it illegal for drivers under age of 21 years to have measurable amounts of alcohol in their blood, resulting in immediate license suspension and fines. Carpenter uses the Behavioral Risk Factor Surveillance System, which includes information on alcohol consumption and drunk driving behavior for young adults over the age of 18 years for the years 1984–2001. He estimates the effects of ZT Laws using the DID approach. The control group is composed of individuals aged 22–24 years who are otherwise similar to treated individuals (18–20-year olds) but who should have been unaffected by the ZT policies. Let dZT be a dummy variable that takes the value 1 if the state has ZT in that year, and 0 otherwise; and dg is a dummy variable that takes the value 1 if the subject is in the treatment group, and 0 otherwise. Alcohol consumption is regressed on dZT, d1820, dZT ×d1820, and other control variables mentioned above. The OLS estimate of the coefficient of dZT × d1820 yields the DID estimator of the ZT laws. Carpenter’s results indicate that the laws reduced heavy episodic drinking (five or more drinks at one sitting) among underage males by 13%. For a recent review of DID health economics applications as well as a summary table of these applications, see Jones (2012).
Random Effects
There are too many parameters in the FE model and the loss of degrees of freedom can be avoided if μi can be assumed random. In this case, μi ~IID(0,σ2μ),vit ~IID(0,σ2v) and the μi is independent of the nit. In addition, the Xit is independent of the μi and vit, for all i and t. This random-effects (RE) model can be estimated by GLS, which can be obtained using a least squares regression of y*it=yit-θyi. on X*it similarly defined. Θ=1-(σv/σ1) where σ21=Tσ2μ+σ2v. The best quadratic unbiased estimators of the variance components depend on the true disturbances, and these are minimum variance unbiased under normality of the disturbances. One can obtain feasible estimates of these variance components by replacing the true disturbances by OLS or FE residuals (see Chapter 2 of Baltagi (2008) for details).
Under the assumption of normality of the disturbances, Breusch and Pagan (1980) derived a Lagrange multiplier (LM) test to test H0; σ2μ=0: The resulting LM statistic requires only OLS residuals and is easy to compute. Under H0, this LM statistic is asymptotically distributed as a x21 (see Chapter 4 of Baltagi (2008) for details.) For the Contoyannis and Rice (2001) application, this LM statistic is 3355.26 and is significant. This means that heterogeneity across individuals is significant and ignoring it as OLS does will lead to misleading inference. The RE estimates are 0.028 for excellent health, 0.013 for good health, and -0.002 for the General Health Questionnaire: Likert Scale score (hlghq1), with only the good health estimate being statistically insignificant.
Hausman Test
A specification test based on the difference between the FE and RE estimators is known as the Hausman test. The null hypothesis is that the individual effects are not correlated with the X`its. The basic idea behind this test is that the FE estimator βFE is consistent, whether or not the effects are correlated with the X`its. This is true because the within transformation yit wipes out the μi’s from the model. However, if the null hypothesis is true, the FE estimator is not efficient under the RE specification because it relies only on the within variation in the data. However, the RE estimator βRE is efficient under the null hypothesis but is biased and inconsistent when the effects are correlated with the X`its. The difference between these estimators q=βFE-βRE tends to zero in probability limits under the null hypothesis and is nonzero under the alternative. The variance of this difference is equal to the difference in variances, var(q)=var(βFE)-var(βRE), because cov(q,βRE )=0 under the null hypothesis. Hausman’s test statistic is based on m=q[var(q)]-1q and is asymptotically distributed as x2K under the null hypothesis. For the Contoyannis and Rice (2001) application, Hausman’s test statistic is 322.39 and is distributed as x229. But the var(q) is not positive definite. Using an alternative computation of this Hausman (1978) test based on an artificial regression, the null hypothesis is rejected and one can infer that the RE estimator is inconsistent and should not be used for inference.
Powell (2009) uses four waves of the 1997 National Longitudinal Survey of Youth and external data to examine the relationship between adolescent body mass index (BMI), fast food prices, and fast food restaurant availability. The OLS estimate of the fast food price elasticity of BMI is -0.095, whereas the RE estimate is 0.084. The latter is closer to the FE estimate of -0.078, but the RE estimator is rejected by the Hausman test. The number of fast food restaurants per capita was not found to be significant.
Hausman And Taylor Estimator
The RE model is rejected because it assumes no correlation between the explanatory variables and the individual effects. The FE estimator, however, assumes that all the explanatory variables are correlated with the individual effects. Instead of this ‘all or nothing’ correlation among the X and the μi, Hausman and Taylor (1981) consider a model where some of the explanatory variables are related to the μi. In particular, they consider the following model:
![]()
where the Zi is cross-sectional time-invariant variable. Hausman and Taylor (1981), hereafter HT, split X and Z into two sets of variables: X= [X1; X2] and Z= [Z1; Z2] where X1 is n ×k1, X2 is n ×k2, Z1 is n×g1, Z2 is n×g2, and n =NT. X1 and Z1 are assumed exogenous in that they are not correlated with μi and vit, whereas X2 and Z2 are endogenous because they are correlated with μi, but not with vit. The Within transformation sweeps the μi and removes the bias, but in the process it would also sweep the Z`is and hence the Within estimator will not give an estimate of y. To get around that, HT suggest obtaining the FE residuals and averaging them over time:
![]()
Then, one can run 2SLS of di on Zi with the set of instruments A= [X1, Z1] to get a consistent estimate of y which is called y2SLS . For this to be feasible, the order condition for identification has to hold (k1≥g2). This means that there has to be as many time-varying (X1) exogenous variables as there are time-invariant endogenous variables (Z2). The intuition here is that every Xit can be written as the sum of Xit=(Xit-Xi) and Xi. It is the latter term that contains μi as it is swept away from the former. If X2 is correlated with μi, it must be in X2 , which makes X2 the ideal instrument. HT use X1 twice because it is exogenous, once as X1 and another time as X1.Z1 is exogenous and Z2 can be instrumented by the additional instruments gained from X1. With consistent estimates of the disturbances obtained from βFE and y2SLS , one can obtain consistent estimates of the variance components and hence θ. This, in turn, allows us to compute y*it=yit-θyi and X*it and Z*=(1-θ)Z. HT suggest an efficient estimator that can be obtained by running 2SLS of y*it on X*it and Z* using AHT=[X,X1,Z1 ] as instruments.
- If k1<g2, then the equation is underidentified. In this case, βHT=βFE and y cannot be estimated.
- If k1=g2, then the equation is just-identified. In this case, βHT=βFE and yHT=y2SLS.
- If k1>g2, then the equation is over-identified and the HT estimator is more efficient than the FE estimator.
A test for over-identification is obtained by computing
![]()
with
![]()
Contoyannis and Rice (2001) applied the HT estimator, choosing race to be exogenous (the only time-invariant Z1) and education to be endogenous (the only time-invariant Z2). They also chose the health variables that are time varying to be endogenous (sahex, sahgd, and hlghq1) as well as (prof, manag, skllnm, and skllm). The HT estimates are 0.013 for excellent health, 0.010 for good health, and -0.003 for the General Health Questionnaire: Likert Scale score (hlghq1), with only the latter estimate being statistically significant.
Dynamic Panel Data Models
Many economic relationships are dynamic in nature and one of the advantages of panel data is that they allow the researcher to better understand the dynamics of adjustment. For example, a key feature of the rational addiction theory studied by Becker, Grossman, and Murphy (1994) is that consumption of cigarettes is addictive and will depend on future as well as past consumption. Consumers are rational if they are forward-looking in the sense that they anticipate the expected future consequences of their current actions. They recognize the addictive nature of their choices but they may elect to make them because the gains from the activity exceed the costs through future addiction. The more they smoke the higher is the current utility derived. However, the individual recognizes that he or she is building up a stock of this addictive good that is harmful. The individual rationally trades off these factors to determine the appropriate level of smoking. Finding future consumption statistically significant is a rejection of the myopic model of consumption behavior. In the latter model of addictive behavior, only past consumption stimulates current consumption, because individuals ignore the future in making their consumption decisions.
More formally, dynamic relationships are characterized by the presence of a lagged dependent variable among the regressors, i.e.,
![]()
where δ is a scalar, x`it is 1×K and β is K×1, where μi~IID(0,σ2μ) and vit~ IID(0,σ2v) independent of each other and among themselves. This dynamic panel data regression model is characterized by two sources of persistence over time. Autocorrelation due to the presence of a lagged dependent variable among the regressors and individual effects characterizing the heterogeneity among the individuals. As yit is a function of μi, it immediately follows that yi,t-1 is also a function of μi, Therefore, yi,t-1 is correlated with the error term. This renders the OLS estimator biased and inconsistent even if the nit are not serially correlated. For the FE estimator, the Within transformation wipes out the μi, but (yi,t-1-yi-1) where yi-1=∑Tt=2yi,t-1/(T-1) will still be correlated with (vit-vi) even if the nit are not serially correlated. This is be- cause yi,t-1 is correlated with vi. by construction. The latter average contains vi,t-1 which is obviously correlated with yi,t-1. In fact, the Within estimator will be biased of O(1/T) and its consistency will depend on T being large (Nickell, 1981). Therefore, for the typical micropanel where N is large and T is fixed, the Within estimator is biased and inconsistent. It is worth emphasizing that only if T→∞ will the Within estimator of δ and β be consistent for the dynamic error component model. For macropanels, some researchers may still favor the Within estimator arguing that its bias may not be large. Judson and Owen (1999) performed some Monte Carlo experiments for N=20 or 100 and T=5, 10, 20, and 30 and found that the bias in the Within estimator can be sizable, even when T=30. This bias increases with d and decreases with T. But even for T=30, this bias could be as much as 20% of the true value of the coefficient of interest.
Arellano and Bond (1991) suggested FD model to get rid of the μi and then using a Generalized Method of Moments (GMM) procedure that utilizes the orthogonality conditions that exist between lagged values of yit and the disturbances vit. It is illustrated with the simple autoregressive model with no regressors. With a three-wave panel, i.e., T=3, the differenced equation becomes:
![]()
In this case, yi1 is a valid instrument because it is highly correlated with (yi2 -yi1) and not correlated with (vi3 -vi2) as long as the nit are not serially correlated. But note what happens if the fourth wave is obtained:
![]()
In this case, yi2 as well as yi1 are valid instruments for (yi3 -yi2) because both yi2 and yi1 are not correlated with (vi4 -vi3). One can continue in this fashion, adding an extra valid instrument with each forward period, so that for period T, the set of valid instruments becomes (yi1, yi2, …, yi,T-2). The optimal Arellano and Bond (1991) GMM estimator of δ utilizes all these moment conditions weighting them by a sandwich heteroskedasticity auto-correlation estimator of the variance–covariance matrix of the disturbances. Arellano and Bond (1991) propose testing for serial correlation for the disturbances of the first-differenced equation. This test is important because the consistency of the GMM estimator relies on the assumption of no serial correlation in the v`its. Additionally, Arellano and Bond (1991) suggest a Sargan test for over-identifying. One has to reject the existence of serial correlation in the v`its and not reject the over-identifying restrictions. Failing these diagnostics renders this procedure inconsistent.
Using Monte Carlo experiments, Bowsher (2002) finds that the use of too many moment conditions causes the Sargan test for overidentifying restrictions to be undersized and have extremely low power. The Sargan test never rejects when T is too large for a given N. Zero rejection rates under the null and alternative were observed for the following (N,T) pairs (125,16), (85,13), and (40,10). This is attributed to poor estimates of the weighting matrix in GMM. Using Monte Carlo experiments, Ziliak (1997) found that there was a bias/efficiency trade-off for the Arellano and Bond (1991) GMM estimator as the number of moment conditions increase and that one is better off with suboptimal instruments. Ziliak attributes the bias in GMM to the correlation between the sample moments used in estimation and the estimated weight matrix.
Blundell and Bond (1998) attributed the bias and the poor precision of the first difference GMM estimator to the problem of weak instruments. They show that an additional mild stationarity restriction on the initial conditions process allows the use of a system GMM estimator which captures additional nonlinear moment conditions that are ignored by the Arellano and Bond (1991) estimator. These additional nonlinear moment conditions are described in Ahn and Schmidt (1995) and can be linearized by adding a set of equations in levels on top of the set of equations in first differences of Arellano and Bond, hence a system of equations (see Baltagi, 2008, Chapter 8, for details). In this case, one uses lagged differences of yit as instruments for equations in levels, in addition to lagged levels of yit as instruments for equations in first differences. The system GMM estimator is shown to have dramatic efficiency gains over the basic first-difference Arellano and Bond GMM estimator as δ→1, i.e., as the process tends to unit root and nonstationarity.
Baltagi et al. (2000) estimate a dynamic demand model for cigarettes based on panel data from 46 American states over the period 1963–92. The estimated equation is:
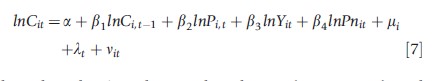
where the subscript i denotes the i-th state (i=1, …, 46), and the subscript t denotes the t-th year (t =1,…,30). Cit is real per capita sales of cigarettes by persons of smoking age (14 years and older). This is measured in packs of cigarettes per head. Pit is the average retail price of a pack of cigarettes measured in real terms. Yit is real per capita disposable income. Pnit denotes the minimum real price of cigarettes in any neighboring state. This last variable is a proxy for the casual smuggling effect across state borders. mi denotes the statespecific effects, and lt denotes the year-specific effects. OLS, which ignores the state and time effects, yields a low short-run price elasticity of -0.09. However, the coefficient of lagged consumption is 0.97 which implies a high long-run price elasticity of -2.98. The FE estimator with both state and time effects yields a higher short-run price elasticity of -0.30, but a lower long-run price elasticity of -1.79. Both state and time dummies were jointly significant with an observed F-statistic of 7.39 and a p-value of .0001. This is a dynamic equation and the OLS and FE estimators do not take into account the endogeneity of the lagged dependent variable. The Arellano and Bond (1991) GMM estimator yields a lagged consumption coefficient estimate of 0.70 and an own price elasticity of -0.40, both highly significant (Baltagi, 2008). The two-step Sargan test for over-identification does not reject the null, but this could be due to the bad power of this test for N=46 and T=28. The test for first-order serial correlation rejects the null of no first-order serial correlation, but it does not reject the null that there is no second-order serial correlation. This is what one expects in a first-differenced equation with the original untransformed disturbances assumed to be not serially correlated. Blundell and Bond (1998) system GMM estimator yields a lagged consumption coefficient estimate of 0.70 and an own price elasticity of -0.42, both highly significant, but with higher standard errors than the corresponding Arellano and Bond estimators. Sargan’s test for over-identification does not reject the null, and the tests for first- and second-order serial correlation yield the expected diagnostics for system GMM.
Scott and Coote (2010) applied the dynamic panel data system GMM estimator to estimate the effect of regional primary-care organizations on primary-care performance. They utilize a panel of 119 Divisions of General Practice in Australia observed quarterly over the period 2000–05. Using four different measures of primary-care performance, a high level of persistence was found. The results show that Divisions were more likely to influence general practice infrastructure than clinical performance in diabetes, asthma, and cervical screening. Other applications of dynamic panel data GMM estimation methods include Baltagi and Griffin (2001) to a rational addiction model of cigarettes and Suhrcke and Urban (2010) to the impact of cardiovascular disease morality on economic growth.
Ng et al. (2012) study the relative importance of diet, physical activity, and health behavior of smoking and drinking on weight for a set of Chinese males, using panel data from the China Health and Nutrition Survey. The authors use a dynamic panel system GMM approach that explicitly includes time and spatially varying community-level urban city and price measures as instruments, to obtain estimates for the effects of diet, physical activity, drinking, and smoking on weight. Results show that approximately 5.4% of weight gain is due to declines in physical activity and 2.8–3.1% is due to dietary changes over time.
Limited Dependent Variable Panel Data Models
In some health studies, the dependent variable is binary. For example, individual i may be in good health at time t, i.e., yit=1 with probability pit; or in bad health, yit= 0 with probability 1-pit. Good health occurs when a latent unobserved index of health y*it is positive

with y*it=x`itβ+μi+vit. So that
![]()
where the last equality holds as long as the density function describing F is symmetric around zero. This is true for the logistic and normal density functions which are the most used in practice. This is a nonlinear panel data model because F is a cumulative density function, and one cannot get rid of the individual effects as in the linear panel data case with a within transformation. Hsiao, 2003 showed that unlike the linear FE panel data case, where the inconsistency of the μ`is did not transmit into inconsistency for the β`s. For the nonlinear panel data case, the inconsistency of the μ`is renders the maximum likelihood estimates of the β`s inconsistent. The usual solution around this incidental parameters problem is to assume a logistic likelihood function and to condition on ∑Tt=1yit, which is a minimum sufficient statistic for mi maximizing the conditional logistic likelihood function
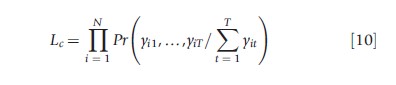
yields the conditional logit estimates for β. By definition of a sufficient statistic, the distribution of the data given this sufficient statistic will not depend on μi. In contrast to the FE logit model, the conditional likelihood approach does not yield computational simplifications for the FE probit model. But the probit specification has been popular for the RE model. In this case, uit=μi+vit where μI~IIN(0,σ2v) and vit~IIN(0,σ2v) independent of each other and the xit Because E(uit uis)= σ2μ for t≠s, the joint likelihood of (y1t, …, yNt) can no longer be written as the product of the marginal likelihoods of the yit. This complicates the derivation of maximum likelihood which will now involve T-dimensional integrals. Fortunately, Butler and Moffitt (1982) showed that for the probit case, the maximum likelihood computations involve only one integral which can be evaluated using the Gaussian–Hermite quadrature procedure. For an early application of the RE probit model, Sickles and Taubman (1986), who estimated a twoequation structural model of the health and retirement decisions of the elderly using five biennial panels of males drawn from the Retirement History Survey. Both the health and retirement variables were limited dependent variables and MLE using the Butler and Moffitt (1982) Gaussian quadrature procedure was implemented. Sickles and Taubman found that retirement decisions were strongly affected by health status and workers not yet eligible for social security were less likely to retire.
Contoyannis et al. (2004) utilize seven waves (1991–97) of the BHPS to analyze the dynamics of individual health and to decompose the persistence in health outcomes in the BHPS data into components due to state dependence, serial correlation, and unobserved heterogeneity. The indicator of health is defined by a binary response to the question: ‘‘Does your health in any way limit your daily activities compared to most people of your age?’’ A sample of 6106 individuals resulting in 42 742 panel observations are used to estimate static and dynamic panel probit models by maximum simulated likelihood methods. The dynamic models show strong positive state dependence.
Hernandez-Quevedoa et al. (2008) use eight waves of the ECHP over the period 1994–2001 to estimate a dynamic nonlinear panel data model of health limitations for individuals within the Member States of the European Union. The RE probit specification conditions on previous health status and parameterizes the unobserved individual effect as a function of initial period observations on time-varying regressors and health (Wooldridge, 2005). Results reveal high state dependence of health limitations, which remains after controlling for measures of socioeconomic status. There is also heterogeneity in the socioeconomic gradient across countries. The importance of regarding health as a dynamic concept has implications for policy development. They imply that medical interventions or health improvement policies that create health gains, will have multiplier effects in the long run.
Further Readings
The panel data econometrics literature has exhibited phenomenal growth and one cannot do justice to the many theoretical contributions to date. Space limitations prevented the inclusion of many worthy topics including attrition, sample selection, semiparametric, nonparametric, and Bayesian methods using panel data. Unbalanced panels, problems associated with heteroskedasticity, serial as well as spatial correlation in panels, measurement error, duration, and quantile panel data models to mention a few. More extensive treatment of these and other topics are given in textbooks on the subject by Baltagi (2008), Wooldridge (2002), and Hsiao (2003). Also see the survey by Imbens and Wooldridge (2009) for an extensive discussion of alternative econometric methods to program evaluation besides the DID method. Also see Angrist and Pischke (2009) for a textbook discussion of DID. For recent applications of panel data methods to health economics, see the special issue of Empirical Economics edited by Baltagi et al. (2012) and Jones (2012).
References:
- Abadie, A. (2005). Semiparametric difference-in-differences estimators. Review of Economic Studies 72, 1–19.
- Abadie, A., Diamond, A. and Hainmueller, J. (2010). Synthetic control methods for comparative case studies: Estimating the effect of California’s tobacco control program. Journal of the American Statistical Association 105, 493–505.
- Abrevaya, J. (2006). Estimating the effect of smoking on birth outcomes using a matched panel data approach. Journal of Applied Econometrics 21, 489–519.
- Ahn, S. C. and Schmidt, P. (1995). Efficient estimation of models for dynamic panel data. Journal of Econometrics 68, 5–27.
- Angrist, J. D. and Pischke, J-S. (2009). Mostly harmless econometrics: An empiricist’s companion. Princeton: Princeton University Press.
- Arellano, M. and Bond, S. (1991). Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. Review of Economic Studies 58, 277–297.
- Askildsen, J. E., Baltagi, B. H. and Holmas, T. H. (2003). Wage policy in the health care sector: A panel data analysis of nurses’ labour supply. Health Economics 12, 705–719.
- Athey, S. and Imbens, G. W. (2006). Identification and inference in nonlinear difference-in-differences models. Econometrica 74, 431–497.
- Baltagi, B. H. (2008). The econometrics of panel data. Chichester: Wiley.
- Baltagi, B. H. and Geishecker, I. (2006). Rational alcohol addiction: Evidence from the Russian longitudinal monitoring survey. Health Economics 15, 893–914.
- Baltagi, B. H. and Griffin, J. M. (2001). The econometrics of rational addiction: The case of cigarettes. Journal of Business and Economic Statistics 19, 449–454.
- Baltagi, B. H., Griffin, J. M. and Xiong, W. (2000). To pool or not to pool: Homogeneous versus heterogeneous estimators applied to cigarette demand. Review of Economics and Statistics 82, 117–126.
- Baltagi, B. H., Jones, A. M., Moscone, F. and Mullahy, J. (2012). Special issue on health econometrics: Editors’ introduction. Empirical Economics 42, 365–368.
- Baltagi, B. H. and Moscone, F. (2010). Health care expenditure and income in the OECD reconsidered: Evidence from panel data. Economic Modelling 27, 804–811.
- Bertrand, M., Duflo, E. and Mullainathan, S. (2004). How much should we trust differences-in-differences estimates? Quarterly Journal of Economics 119, 249–275.
- Besley, T. and Case, A. (2000). Unnatural experiments? Estimating the incidence of endogenous policies. Economic Journal 110, F672–F694.
- Blundell, R. and Bond, S. (1998). Initial conditions and moment restrictions in dynamic panel data models. Journal of Econometrics 87, 115–143.
- Bowsher, C. G. (2002). On testing over identifying restrictions in dynamic panel data models. Economics Letters 77, 211–220.
- Breusch, T. S. and Pagan, A. R. (1980). The Lagrange multiplier test and its applications to model specification in econometrics. Review of Economic Studies 47, 239–253.
- Butler, J. S. and Moffitt, R. (1982). A computationally efficient quadrature procedure for the one factor multinomial probit model. Econometrica 50, 761–764.
- Card, D. (1990). The impact of the Mariel boat lift on the Miami labor market. Industrial and Labor Relations Review 43, 245–253.
- Carpenter, C. (2004). How do zero tolerance drunk driving laws work? Journal of Health Economics 23, 61–83.
- Conley, T. G. and Taber, C. R. (2011). Inference with ‘‘Difference-in-Differences’’ with a small number of policy changes. Review of Economics and Statistics 93, 113–125.
- Contoyannis, P., Jones, A. M. and Rice, N. (2004). The dynamics of health in the British Household Panel Survey. Journal of Applied Econometrics 19, 473–503.
- Contoyannis, P. and Rice, N. (2001). The impact of health on wages: Evidence from the British Household Panel Survey. Empirical Economics 26, 599–622.
- Donald, S. G. and Lang, K. (2007). Inference with difference in differences and other panel data. Review of Economics and Statistics 89, 221–233.
- Greene, W. (2010). Distinguishing between heterogeneity and inefficiency: Stochastic frontier analysis of the World Health Organization’s panel data on national health care systems. Health Economics 13, 959–980.
- Gruber, J. and Poterba, J. (1994). Tax incentives and the decision to purchase health insurance: Evidence from the self-employed. Quarterly Journal of Economics 109, 701–734.
- Hansen, C. B. (2007). Generalized least squares inference in panel and multilevel models with serial correlation and fixed effects. Journal of Econometrics 140, 670–694.
- Hausman, J. A. (1978). Specification tests in econometrics. Econometrica 46, 1251–1271.
- Hausman, J. A. and Kuersteiner, G. (2008). Difference in difference meets generalized least squares: Higher order properties of hypotheses tests. Journal of Econometrics 144, 371–391.
- Hausman, J. A. and Taylor, W. E. (1981). Panel data and unobservable individual effects. Econometrica 49, 1377–1398.
- Herna´ndez-Quevedoa, C., Jones, A. M. and Rice, N. (2008). Persistence in health limitations: A European comparative analysis. Journal of Health Economics 27, 1472–1488.
- Hsiao, C. (2003). Analysis of panel data. Cambridge: Cambridge University Press.
- Imbens, G. W. and Wooldridge, J. M. (2009). Recent developments in the econometrics of program evaluation. Journal of Economic Literature 47, 5–86.
- Janke, K., Propper, C. and Henderson, J. (2009). Do current levels of air pollution kill? The impact of air pollution on population mortality in England. Health Economics 18, 1031–1055.
- Jones, A. M. (2012). Panel data methods and applications to health economics. In Terence, C., Mills and Patterson, Kerry (eds.) Handbook of econometrics volume II: Applied econometrics, pp. 557–631. Basingstoke: Palgrave MacMillan.
- Judson, R. A. and Owen, A. L. (1999). Estimating dynamic panel data models: A guide for macroeconomists. Economics Letters 65, 9–15.
- Laporte, A. and Windmeijer, F. (2005). Estimation of panel data models with binary indicators when treatment effects are not constant over time. Economics Letters 88, 389–396.
- Meyer, B., Viscusi, K. and Durbin, D. (1995). Workers’ compensation and injury duration: Evidence from a natural experiment. American Economic Review 85, 322–340.
- Ng, S. W., Norton, E. C., Guilkey, D. K. and Popkin, B. M. (2012). Estimation of a dynamic model of weight. Empirical Economics 42, 413–433.
- Nickell, S. (1981). Biases in dynamic models with fixed effects. Econometrica 49, 1417–1426.
- Powell, L. M. (2009). Fast food costs and adolescent body mass index: Evidence from panel data. Journal of Health Economics 28, 963–970.
- Ruhm, C. J. (1996). Alcohol policies and highway vehicle fatalities. Journal of Health Economics 15, 435–454.
- Sickles, R. C. and Taubman, P. (1986). A multivariate error components analysis of the health and retirement study of the elderly. Econometrica 54, 1339–1356.
- Stock, J. H. and Watson, M. W. (2008). Heteroskedasticity-robust standard errors for fixed effects panel data regression. Econometrica 76, 155–174.
- Suhrcke, M. and Urban, D. (2010). Are cardiovascular diseases bad for economic growth? Health Economics 19, 1478–1496.
- Wooldridge, J. M. (2002). Econometric analysis of cross section and panel data, XXIII, pp. 752. Cambridge, Mass: MIT Press.
- Wooldridge, J. M. (2005). Simple solutions to the initial conditions problem in dynamic, nonlinear panel data models with unobserved heterogeneity. Journal of Applied Econometrics 20, 39–54.
- Ziliak, J. P. (1997). Efficient estimation with panel data when instruments are predetermined: An empirical comparison of moment-condition estimators. Journal of Business and Economic Statistics 15, 419–431.