Most empirical research in health economics is conducted with the goal of providing causal evidence of the effect of a particular variable (the causal variable – X) on an outcome of interest (Y). Such analyses are typically conducted in the context of explaining past behavior, testing an economic theory, or to evaluating a past or prospective policy. Common to all such applied contexts is the need to infer the effect of a counterfactual ceteris paribus exogenous change in X on Y, using statistical results obtained from survey data in which observed differences in X are neither ceteris paribus nor exogenous. In such nonexperimental sampling circumstances, statistical methods that essentially measure observed differences in Y per observed differences in X typically miss the mark because they fail to control for unobserved variables that are correlated in sampling with both X and Y. Such unobserved confounding variables, which vary in sampling with both X and Y, obfuscate the true causal effect (TCE) as it would have manifested if the value of X were exogenously perturbed ceteris paribus. Consider, for instance, attempting to obtain inference regarding the effect of cigarette smoking during pregnancy on infant birth weight using survey data. Suppose there exists an unobserved variable, say ‘health mindedness’ that causes pregnant women to both refrain from smoking and engage in other healthy prenatal behaviors. In such a scenario it is possible that observed smoking levels could be negatively associated with birth weight even though a ceteris paribus exogenous change in smoking (as might be brought about through policy intervention) would have no causal effect on birth weight. The present article discusses available regression methods designed not only to control for observable confounding influences but also to account for the presence of unobservables that would otherwise thwart causal inference.
The remainder of the article is organized as follows. The next section offers a more formal discussion of estimation bias due to unobserved confounding. In Section Instrumental Variables Methods, we consider a commonly implemented remedy for such bias – the use of instrumental variables (IV). Therein extant IV methods for both linear and nonlinear models are reviewed. The article concludes with a summary and some recommendations.
Unobserved Confounder Bias
At issue here is the presence of confounding variables which serve to mask the TCE of X on Y. The author begins by defining a confounder as a variable that is correlated with both Y and X. Confounders may be observable or unobservable (denoted Co and Cu, respectively, – in the present discussion both are assumed to be scalars (i.e., not vectors)). In modeling Y, if the presence of Cu cannot be legitimately ruled out, then X is said to be endogenous. Observations on Co can be obtained from the survey data, so its influence can be controlled in estimation of the TCE. Cu, however, cannot be directly controlled and, if left unaccounted for, will likely cause bias in statistical inference regarding the TCE. This happens because estimation methods that ignore the presence of Cu will spuriously attribute to X observed differences in Y that are, in fact, due to Cu. The author refer to such bias as unobserved confounder bias (henceforth Cu–bias) (sometimes called endogeneity bias, hidden selection bias, or omitted variables bias). One can formally characterize Cu–bias in a useful way. For simplicity of exposition, the author casts the true causal relationship between X and Y as linear and write
![]()
where β is the parameter that captures the TCE, βo and βu are parametric coefficients for the confounders, and e is the random error term (without loss of generality, it can be assumed that the Y intercept is 0). In the naive approach to the estimation of the TCE (ignoring the presence of Cu), the ordinary least squares (OLS) method is applied to
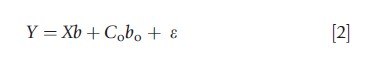
where the β’s are parameters and ε is the random error term. The parameter b is taken to represent the TCE. It can be shown that OLS will produce an unbiased estimate of b (here and henceforth, when the author refers to unbiasedness it is done so in the context of large samples). It is also easy to show, however, that

where bXCu is a measure of the correlation between Cu and X. As is clear from eqn [3], Cu bias in OLS estimation is bXCuβu , which has two salient components: the correlation between the unobserved confounder and the causal variable of interest and the correlation between the unobserved confounder and the outcome. Equation [3] is helpful because it can be used to diagnose potential Cu bias. Consider the smoking (X) and birth weight (Y) example discussed in the Section Introduction, in which Cu is health mindedness. In this case one would expect that bXCu would be negative and that βu would be positive. The net effect of which would be negative Cu bias in the estimation of the TCE via OLS.
Clearly an approach to estimation is needed that, unlike OLS, does not ignore the presence and potential bias of Cu. One such approach exploits sample variation in a particular type of variable (a so-called IV) to eliminate bias due to correlation between Cu and X (Cu bias as characterized in eqn [3]). This is the subject of the following section.
Instrumental Variables Methods
As eqn [3] demonstrates, if the correlation link between the causal variable and the unobservable confounder were somehow broken, concomitant estimation bias would be eliminated. If the researcher could exert control over the sampled values of X, then such disjunction of Cu and X could be accomplished by random assignment of X values to the individual sample members. Under such randomization, bXCu would be equal to zero, by eqn [3] β would be equal to β, and conventional estimation methods like OLS, which ignore the presence of Cu, would be unbiased. Unfortunately, in applied health economics and health services research, as in other social sciences, explicit randomization (experimentation) is often prohibitively costly or ethically infeasible. A form of pseudorandomization is, however, possible in the context of survey (nonexperimental) data. If, for instance, a variable that is observed as one of the survey items is highly correlated with X but correlated with neither Y nor Cu (except through its correlation with X), then the sample variation (across observations) in the value of that variable can be viewed as providing variation in X that is not correlated with Cu – a kind of pseudorandomization for X. Such a variable is typically called an IV. In the context of our smoking birth weight example, cigarette tax is an arguably valid IV in that it should be highly correlated with cigarette consumption but not directly correlated with birth weight.
IV estimation methods all require observable confounder (Co) control – typically within a regression framework akin to eqn [1]. Most often, however, the linear regression model in eqn [1] is not realistic in that it precludes cases in which the relationship between Y and the right-hand side variables (X, Co, and Cu) is nonlinear – for example, when Y is limited in range (e.g., nonnegative and binary outcomes); and/or when such characteristics of the outcome induce interactions among the causal variable and confounders. In the following, the presence of a valid IV (call it W) in the relevant survey is assumed and IV estimation methods for both linear and nonlinear contexts are considered.
Instrumental Variables Estimation In Linear Models
By way of motivating the conventional linear IV estimator in the context of eqn [1], the author examines the underpinnings of the OLS estimator of the TCE for the case in which βu=0 (i.e., the case in which there is no unobservable confounder). When βu=0, eqn [1] becomes
![]()
and the formulation of the OLS estimator of β (and βo), which involves data on observable variables only (viz., X and Co), can be derived from the fact that X and Co are not correlated with the error term e. A similar tack cannot, however, be taken when βu≠0. In this case, eqn [1] can be rewritten as
![]()
where e*=Cuβu +e, and although Co and e* are arguably uncorrelated, the correlation between X and e* is clearly nonzero because X and C are, by the definition of the term confounder, correlated. As a consequence of the undeniable correlation between X and Cu, the aforementioned derivation of the OLS estimator cannot be replicated for eqn [5]. This approach is not, however, entirely futile if an IV (W) is available in the data. By definition, the IV W is uncorrelated with both Cu and e. W is, therefore, not correlated with e* so, analogous to the derivation of the OLS estimator based on eqn [4], it can be used to formulate an unbiased estimator of β and βo (the so-called IV estimator). The IV estimator is available in all of the most widely used statistical and econometric software packages (e.g., Stata and SAS).
There are two relatively more intuitive two-stage versions of the IV estimator. Both of these approaches implement an auxiliary regression of the form
![]()
where the a’s are parameters. In the first stage of each of these methods, OLS is applied to eqn [6] to obtain estimates of parameters ( ao and aw ) and the regression predictor of X (X= Coao+Waw ). One of these methods, called two-stage least squares (2SLS) has as its second stage the OLS estimation of β and βo via eqn [5] with X substituted for X. The other approach, called two-stage residual inclusion (2SRI) calls for OLS estimation of
![]()
where Cu=X-(Coao+Waw) – i.e., the residual from firststage OLS estimation of eqn [6].
When true causal model is eqn [1] both 2SLS and 2SRI produce estimates of the TCE (β) and βo that are identical to those obtained via the IV estimator.
Instrumental Variables Estimation In Nonlinear Models
Although the linear IV estimator (or its equivalent versions 2SLS or 2SRI) is intuitive and simple to apply due to its availability, the linear true causal model (as specified in eqn [1]) on which it is based does not conform to most empirical contexts in health economics. In most applied settings, the range of the outcome is limited in a way that makes a nonlinear specification of the true causal model more sensible. For example, the researcher is often interested in estimating the causal effect of a policy variable (X) on whether or not an individual will engage in a specified health-related behavior. In this case, the outcome of interest is binary so that a nonlinear specification of the true causal model would likely be more appropriate. In the smoking birth weight example discussed in the Section Introduction, the outcome of interest (birth weight) is nonnegative and an exponential regression specification of the true causal model is more in line with this feature of the data than is the linear specification in eqn [1]. Another common example of inherent nonlinearity in health economics and health services research, is in the modeling of healthcare expenditure or utilization (E/U). It is typical to observe a large proportion of zero values for the E/U outcome. In this and similar empirical contexts, the two-part model (2PM) has been widely implemented. The 2PM allows the process governing observation at zero (e.g., whether or not the individual uses the healthcare service) to systematically differ from that which determines nonzero observations (e.g., the amount the individual uses (or spends on) the service conditional on at least some use). The former can be described as the hurdle component of the model, and the latter is often called the levels part of the model. Both of these components are nonlinear – binary response model for the hurdle; nonnegative regression for E/U levels given some utilization.
To accommodate these and other cases, the generic nonlinear version of the true causal model in eqn [1] is written as
![]()
where μ(X, Co, Cu; θ) is known except for the parameter vector θ. It is very often assumed that μ(X, Co, Cu; θ)=M(Xβ+Coβo+Cuβu), where M( ) is a known function and θ= (β βo βu). In this linear index form the true causal models corresponding to binary and nonnegative outcomes are commonly written, respectively, as
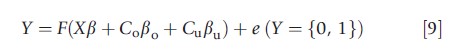
and
![]()
where F( ) is a function whose range is the unit interval. It is noted here that for the generic nonlinear model characterized by eqn [8] the TCE is not embodied in any particular parameter (e.g., β) as in the linear models defined by eqn [1]. Instead, the TCE will be a nonlinear function of all parameters (θ) and all of the right-hand side variables (X, Co, Cu) of the model. Moreover, the exact form of the TCE in nonlinear settings will differ depending on the researcher’s policy relevant analytic objective(s). These issues will not, however, be discussed here. In the present discussion, focus is on estimation of the vector of parameters θ.
In the remainder of this section, various approaches to the estimation of θ in nonlinear models of the generic form given in eqn [8] are examined. The author begins by examining the feasibility and appropriateness of the generalized method of moments (GMM) estimator – the nonlinear analog to IV estimation in the linear model. Next, the nonlinear counterparts to the linear 2SLS and 2SRI are examined. Nonlinear 2SRI (N2SRI) is a member of a class estimators called control function estimators. Other control function estimators that are specifically designed for cases involving binary causal variables are discussed. This section concludes with a description of cases in which the maximum-likelihood method can be applied.
The Generalized Method Of Moments
To estimate of the parameters of nonlinear causal models like eqn [8], one may seek to apply the GMM as an extension of the linear IV approach, detailed in Section Instrumental Variables Estimation in Linear Models. Recall that the derivation in that section relied on two facts:
- Equation [1] could be rewritten as eqn [5] – a linear regression representation involving observable variables only and an additive error term.
- The IV W is correlated with neither Cu (the unobservable confounder) nor e (the random error term in eqn [1]).
Unfortunately, there is only one case (that we know of) in which such a derivation is feasible in the context of eqn [8] – the exponential regression version of the model given in eqn [10]. This model is discussed later. In (all?) other cases, it is the nonadditive involvement of Cu in eqn [8] that makes the derivation of a GMM-type estimator infeasible. The generic nonlinear form of μ( ) precludes reformulation of the model as the sum of a nonlinear parametric component in the observable right-hand side data (X and Co) with an additive error term. Some have suggested the use of an approximation to eqn [8] in which Cu is artificially cast in an additive role in the respecification of the model. For example, following this approach, models like eqn [9] would be rewritten as:
![]()
In which case, the IV condition that W is correlated with neither Cu nor e† would be sufficient to establish the appropriate GMM estimator. Clearly, however, eqns [9] and [11] are not equal; and the argument in favor of eqn [11] as a good approximation to eqn [9] is, at best, strained. Moreover, TCE estimation methods that incorporate GMM results obtained from such additive approximations are clearly biased. The extent of this bias has yet to be investigated.
As mentioned earlier, the only nonlinear context (of which one is aware) in which conditions like (1) and (2) are sufficient for derivation of an unbiased (in large samples) GMM estimator is the linear-index exponential case given in eqn [10]. Not only does this GMM estimator yield unbiased estimates of β and βo but also unlike the additive approximations discussed earlier and exemplified in eqn [11], the exponential GMM results can be used to obtain unbiased estimates of the various policy relevant versions of the TCE.
Two-Stage Control Function Methods
In the Section The generalized method of moments, it is noted that extending the linear IV method to the generic nonlinear model in eqn [8] (i.e., the GMM estimator) is not generally feasible. Therefore, aside from the exponential case, we need a desirable (unbiased) feasible alternate to GMM. In search for such an alternative one turns to the discussion of the linear model in Section Instrumental Variables Estimation in Linear Models wherein the 2SLS and 2SRI estimators for b and bo in eqn [1] are detailed. These estimators yield results identical to those produced by the linear IV method. Consider the feasible nonlinear analogs to linear 2SLS and 2SRI estimation. In the generic nonlinear context eqn [8] is supplemented with the following nonlinear analog to eqn [6]
![]()
In 2SLS and 2SRI, the parameters of eqn [12] (a) are first estimated using an appropriate nonlinear regression estimator (e.g., nonlinear least squares (NLS)) and the following predictor of X is computed

Where a denotes the parameter estimates. In the second stage of the nonlinear analog to 2SLS, an appropriate nonlinear regression estimator (e.g., NLS) would be applied to eqn [8] with the predictor X^ substituted for X (this has also been called the two-stage predictor substitution (2SPS) estimator). In the second stage of the nonlinear analog to 2SRI, instead of substituting the predictor for X in eqn [8], Cu is replaced by the residual from eqn [13] (Cu=X-r(Co ,W; a)) and an appropriate nonlinear regression estimator (e.g., NLS) is applied to the following version of eqn [8]
![]()
where e2SRI is the relevant regression error term. Unlike the linear case, the 2SPS and 2SRI estimators are not identical. Note that the actual value of X is used in eqn [14]. The 2SRI estimator is generally unbiased but the 2SPS estimator is not.
The 2SRI estimator is member of a general class of models called control function methods in which a specified function of the IV (W) (and some parameters) is used to ‘control’ for unobserved confounder bias. In the special (but very common) case in which X is binary, an alternative control function method is available. In this alternative control function framework eqns [8] and [12] are respectively replaced by
![]()
and
![]()
where I(A) is equal to 1 if condition A holds and 0 otherwise, and the probability distribution of Cu* is known. For example, if Cu* is assumed to be logistically distributed, eqn [16] defines a conventional logit model. Similarly if Cu* is normal eqn [16] is tantamount to a probit model. Given the known distribution of Cu* , it can be ‘integrated out’ of eqn [15] and the resultant regression form can be used as the basis for nonlinear estimation (e.g., NLS) estimation of θ. When eqn [15] is linear and Cu* is normally distributed, this control function method coincides with the classical Heckman-type dummy endogenous variable model estimator. Note that both 2SRI and this nonlinear extension of the Heckman approach are feasible and unbiased when X is binary (assuming, of course, that the respective sets of underlying assumptions hold).
Maximum-Likelihood Methods
When Y is a binary probit outcome and C is normally distributed, the control function approach described in the Section Two-stage control function methods leads to the bivariate probit model. In this case, the parameters of the model can be estimated using the maximum-likelihood method. Maximumlikelihood methods are also available for the special case in which the auxiliary regression is linear (akin to eqn [6]) and the outcome regression is a normal-based limited dependent variable model (e.g., probit or Tobit). These methods require joint normality of the random error terms in the outcome and auxiliary regressions.
Common factor models have also been suggested for the case in which X is qualitative. In these models, conditional on an unobserved ‘common factor’ (and the other conditioning variables), Y and X are assumed to be independently distributed. Moreover, these independent distributions and the distribution of the common factor are assumed to be of known form. The maximum-likelihood method can be used to obtain estimates of the parameters in this framework.
Summary
The most widely applied remedy for endogeneity in a causal modeling framework is the conventional linear IV (LIV) estimator described in Section Instrumental Variables Estimation in Linear Models. The popularity of LIV can be attributed to its off-the-shelf software availability, and to its intuitive appeal when cast as a two-stage method – 2SLS or 2SRI. The most attractive feature of LIV is that it need not be estimated in two stages and therefore does not require the specification of an auxiliary regression like eqn [6]. Very often, however, in applied health economics and health services research, endogeneity must be confronted in inherently nonlinear empirical contexts. For example, binary response outcomes, limited dependent variables, and two-part models with endogenous causal regressors abound in these fields. One might think that the GMM, which is the most direct approach to extending the LIV estimator to the nonlinear case, would provide a solution to the unobserved confounding problem in nonlinear models. Unfortunately, except for exponential regression models, the GMM is not feasible as a means of dealing with endogeneity in nonlinear settings.
The easiest to implement approach for such cases is the extension of the linear 2SRI estimator to nonlinear models. The primary drawback to the use of N2SRI is that it requires the specification and estimation of an auxiliary regression as defined in eqn [12]. The main advantages of N2SRI are that it can be applied in any nonlinear regression context and will produce unbiased estimates of the regression parameters (and, therefore, the relevant TCE) under general conditions.
There are alternatives to N2SRI for some specific cases. When the outcome is binary, the nonlinear extension to Heckman-type control functions can be used. These methods, although feasible, are not as simple to apply as N2SRI. A similar criticism holds for the maximum-likelihood common factor models.
When the outcome is limited in range (e.g., probit and Tobit) and the auxiliary regression is linear, maximumlikelihood methods can be applied. These methods, though packaged in Stata and therefore easy to apply, require the relatively strong assumption of joint normality between the outcome and the causal variable. N2SRI imposes no such joint distribution assumptions. Moreover, it is often difficult to justify the linearity of the auxiliary regression and the implied normality of the causal variable. It is typical, that the causal variable will itself be limited in range (e.g., binary and nonnegative), making both linearity and normality implausible.
Simulation-based performance comparisons of the models discussed in this article have yet to be conducted.
References:
- Blundell, R. W. and Smith, R. J. (1989). Estimation in a class of simultaneous equation limited dependent variable models. Review of Economics and Statistics 56, 37–58.
- Blundell, R. W. and Smith, R. J. (1993). Simultaneous microeconometric models with censored or qualitative dependent variables. In Maddala, G. S., Rao, C. R. and Vinod, H. D. (eds.) Handbook of statistics, vol. 2, pp. 1117–1143. Amsterdam: North Holland Publishers.
- Deb, P. and Trivedi, P. K. (2006). Specification and simulated likelihood estimation of a non-normal treatment-outcome model with selection: Application to health care utilization. Econometrics Journal 9, 307–331.
- Heckman, J. (1978). Dummy endogenous variables in a simultaneous equation system. Econometrica 46, 931–959.
- Mullahy, J. (1997). Instrumental-variable estimation of count data models: Applications to models of cigarette smoking behavior. Review of Economics and Statistics 79, 586–593.
- Rivers, D. and Vuong, Q. H. (1988). Limited information estimators and exogeneity tests for simultaneous probit models. Journal of Econometrics 39, 347–366.
- Smith, R. J. and Blundell, R. W. (1986). An exogeneity test for a simultaneous equation Tobit model with an application to labor supply. Econometrica 54, 679–685.
- Terza, J. V. (1998). Estimating count data models with endogenous switching: Sample selection and endogenous treatment effects. Journal of Econometrics 84, 129–154.
- Terza, J. V. (2006). Estimation of policy effects using parametric nonlinear models: A contextual critique of the generalized method of moments. Health Services and Outcomes Research Methodology 6, 177–198.
- Terza, J. V. (2009). Parametric nonlinear regression with endogenous switching. Econometric Reviews 28, 555–580.
- Terza, J. V., Basu, A. and Rathouz, P. (2008). Two-stage residual inclusion estimation: Addressing endogeneity in health econometric modeling. Journal of Health Economics 27, 531–543.