This article presents inference for many commonly used estimators – least squares, generalized linear models, generalized method of moments (GMM), and generalized estimating equations – that are asymptotically normally distributed. Section Inference focuses on Wald confidence intervals and hypothesis tests based on estimator variance matrix estimates that are heteroskedastic-robust and, if relevant, cluster-robust. Section Model Tests and Diagnostics summarizes tests of model adequacy and model diagnostics. Section Multiple Tests presents family-wise error rates and false discovery rates (FDRs) that control for multiple testing such as subgroup analysis. Section Bootstrap and Other Resampling Methods presents bootstrap and other resampling methods that are most often used to estimate the variance of an estimator. Bootstraps with asymptotic refinement are also presented.
Inference
Most estimators in health applications are m-estimators that solve estimating equations of the form

where θ is a q×1 parameter vector, i denotes the ith of N observations, gi(·) is a q×1 vector, and often gi(θ)= gi(yi,xi,θ) where y denotes a scalar-dependent variable and x denotes the regressors or covariates. For ordinary least squares, for example, gi(β)=(yi-x`iβ)xi . Nonlinear least squares, maximum likelihood (ML), quantile regression, and just-identified instrumental variables estimators are m-estimators. So too are generalized linear model estimators, extensively used in biostatistics, that are quasi-ML estimators based on exponential family distributions, notably Bernoulli (logit and probit), binomial, gamma, normal, and Poisson.
The estimator ^y is generally consistent if E[gi(θ) = 0]. Statistical inference is based on the result that θ is asymptotically normal with mean y and variance matrix V[θ] that is estimated by

where N-1A and N-1B are consistent estimates of A= E[N-1∑iHi(θ)] , where Hi(θ)=δgi(θ)/δθ` and B=E[N-1∑i∑igi(θ)gi(θ)`] . The variance is said to be of ‘sandwich form,’ because B^ is sandwiched between A-1 and A-1` . The estimate A^ is the observed Hessian ∑iHi(θ), or in some cases the expected HessianE[∑iHi(θ)]|θ. By contrast, the estimate B, and hence V[θ] in eqn [2], can vary greatly with the type of data being analyzed and the associated appropriate distributional assumptions.
Default estimates of V[θ] are based on strong distributional assumptions, and are typically not used in practice. For ML estimation with density assumed to be correctly specified B=-A, so the sandwich estimate simplifies to V [θ]=-A-1. Qualitatively similar simplification occurs for least squares and instrumental variables estimators when model errors are independent and homoskedastic.
More generally, for data independent over i, B= (N/N-q)∑igi(θ)gi(θ)`, where the multiple N/(N-q) is a commonly used finite sample adjustment. Then the variance matrix estimate in eqn [2] is called the Huber, White, or robust estimate – a limited form of robustness as independence of observations is assumed. For OLS, for example, this estimate is valid even if independent errors are heteroskedastic, whereas the default requires errors to be homoskedastic.
Often data are clustered, with observations correlated within a cluster but independent across clusters. For example, individuals may be clustered within villages or hospitals, or students clustered within class or within school. Let c denote the typical cluster, and sum gi(θ) for observations i in cluster c to form gc(θ). Then B=(C/C-1)∑Cc=1gc(θ)gc(θ)`, where C is the number of clusters, and the variance matrix estimate in eqn [2] is called a cluster-robust estimate. The number of clusters should be large as the asymptotic theory requires C→∞, rather than N→∞. The clustered case also covers short panels with few time periods and data correlated over time for a given individual but independent across individuals. Then the clustering sums over time periods for a given individual. Wooldridge (2003) and Cameron and Miller (2011) survey inference with clustered data.
Survey design can lead to clustering. Applied biostatisticians often use survey estimation methods that explicitly control for the three complex survey complications of weighting, stratification, and clustering. Econometricians instead usually assume correct model specification conditional on regressors (or instruments), so that there is no need to weight; ignore the potential reduction in standard error estimates that can occur with stratification; and conservatively control for clustering by computing standard errors that cluster at a level such as a state (region) that is usually higher than the primary sampling unit.
For time series data, observations may be correlated over time. Then the heteroskedastic and autocorrelation consistent (HAC) variance matrix estimate is used; see Newey and West (1987). A similar estimate can be used when data are spatially correlated, with correlation depending on the distance and with independence once observations are more than a given distance apart. This leads to the spatial HAC estimate; see Conley (1999).
Note that in settings where robust variance matrix estimates are used, additional assumptions may enable more efficient estimation of y such as feasible generalized least squares and generalized estimating equations, especially if data are clustered.
Given θ asymptotic normal with variance matrix estimated using eqn [2], the Wald method can be used to form confidence intervals and perform hypothesis tests.
Let θ be a scalar component of the parameter vector θ. Since θa~ N[θ,V[θ]], we have θa~N[θ, s2θ], where the standard error sθ is the square root of the relevant diagonal entry in V[θ]. It follows that (θ-θ)/sθ ~N[0,1]. This justifies the use of the standard normal distribution in constructing confidence intervals and hypothesis tests for sample size N→∞. A commonly used finite-sample adjustment uses (θ-θ)/sθ~T(N-q), where T(N-q) is the students T distribution with (N-q) degrees of freedom, N is the sample size, and K parameters are estimated.
A 95% confidence interval for y gives a range of values that 95% of the time will include the unknown true value of θ. The Wald 95% confidence interval is θ±c.025×sθ, where the critical value c.025 is either z[.025] = 1.96, the .025 quantile of the standard normal distribution, or t[.025] the .025 quantile of the T(N-q) distribution. For example, c.025 = 2.042 if N-q=30.
For two-sided tests of H0:θ=θ*against Ha:θ≠θ*, the Wald test is based on how far [θ-θ*] is from zero. On normalizing by the standard error, the Wald statistic w=(θ-θ*)/sθ is asymptotically standard normal under H0, though again a common finite sample correction is to use the T(N-q) distribution. H0 at the 5% significance level is rejected if |w|>c.025. Often θ*=0, in which case w is called the t-statistic and the test is called a test of statistical significance. Greater information is conveyed by reporting the p-value, the probability of observing a value of w as large or larger in absolute value under the null hypothesis. Then p=Pr[|W|>|w|], where W is standard normal or T(N-q) distributed. H0:θ=θ* is rejected against H0:θ=θ* at level 0.05 if p<.05.
More generally, it may be interesting to perform joint inference on more than one parameter, such as a joint test of statistical significance of several parameters, or on functions(s) of the parameters. Let h(θ) be an h×1 vector function of y, possibly nonlinear, where h r q. A Taylor series approximation yields h(θ)≈h(θ)+R(θ-θ), where R=δh(θ)/δθ`|θ is assumed to be of full rank h (the nonlinear analog of linear dependence of restrictions). Given θ-θa~N[0,v[θ]], this yields h(θ)a~N[h(θ),RV[θ]R`]. The term delta method is used as a first derivative and is taken in approximating h(θ):
Confidence intervals can be formed in the case that h(·) is a scalar. Then h(θ)±c.025 ×[RV(θ)R`]1/2 is used. A leading example is a confidence interval for a marginal effect in a nonlinear model. For example, for E[y|x]=exp(x`θ) the marginal effect for the jth regressor is δE[y|x]/δxj=exp(x`θ)θj. When evaluated at x=x* this equals exp(x*θ)θj which is a scalar function h(θ) of θ; the corresponding average marginal effect is ∑iexp(xiθ)θj.
A Wald test of H0:h(θ)=0 against Ha:h(θ)≠0 is based on the closeness of h(θ) to zero, using
![]()
under H0. H0 at level 0.05 is rejected if w>x2.95(h). An F version of this test is F=w/h, and is rejected at level 0.05 if w> F.95(h,N-q). This is a small sample variation, analogous to using the T(N-q) rather than the standard normal.
For ML estimation the Wald method is one of the three testing methods that may be used. Consider testing the hypothesis that h(θ)=0. Let θ denote the ML estimator obtained by imposing this restriction, whereas θ does not impose the restriction. The Wald test uses only θ and tests the closeness of h(θ) to zero. The log-likelihood ratio test is based on the closeness of L(θ) to L(θ), where L(θ) denotes the log-likelihood function. The score test uses only θ and is based on the closeness to zero of δL(θ)/δθ|θ, where L(θ) here is the log-likelihood function for the unrestricted model.
If the likelihood function is correctly specified, a necessary assumption, these three tests are asymptotically equivalent. So the choice between them is one of convenience. The Wald test is most often used, as in most cases ^y is easily obtained. The score test is used in situations in which estimation is much easier when the restriction is imposed. For example, in a test of no spatial dependence versus spatial dependence, it may be much easier to estimate y under the null hypothesis of no spatial dependence. The Wald and score tests can be robustified. If one is willing to make the strong assumption that the likelihood function is correctly specified, then the likelihood ratio test is preferred due to the Neyman–Pearson lemma and because, unlike the Wald test, it is invariant to reparameterization.
GMM estimators are based on a moment condition of the form E[gi(θ)] = 0. If there are as many components of g(·) as of θ the model is said to be just identified and the estimate θ solves ∑igi(θ)=0, which is eqn [1]. Leading examples in the biostatistics literature are generalized linear model estimators and generalized estimating equations estimators. If instead there are more moment conditions than parameters there is no solution to eqn [1]. Instead make ∑igi(θ) as close to zero as possible using a quadratic norm. The method of moments estimator minimizes
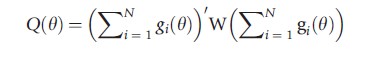
where W is a symmetric positive definite weighting matrix and the best choice of W is the inverse of a consistent estimate of the variance of ∑igi(θ).
The leading example of this is two-stage least-squares (2SLS) estimation for instrumental variables estimation in overidentified models. Then gi(β)=zi(yi-x`iβ), and it can be shown that the 2SLS estimator is obtained if W=(Z`Z)-1. The estimated variance matrix is again of sandwich form eqn [2], though the expressions for A and B are more complicated. For instrumental variables estimators with instruments weakly correlated with regressors an alternative asymptotic theory may be warranted. Bound et al. (1995) outline the issues and Andrews et al. (2007) compare several different test procedures.
Model Tests And Diagnostics
The most common specification tests imbed the model under consideration into a larger model and use hypothesis tests (Wald, likelihood ratio, or score) to test the restrictions that the larger model collapses to the model under consideration. A leading example is test of statistical significance of a potential regressor.
A broad class of tests of model adequacy can be constructed by testing the validity of moment conditions that are imposed by a model but have not already been used in constructing the estimator. Suppose a model implies the population moment condition
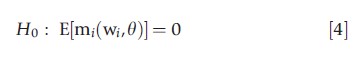
where w is a vector of observables, usually the dependent variable y, regressors x, and, possibly, additional variables z. An m-test, in the spirit of a Wald test, is a test of whether the corresponding sample moment
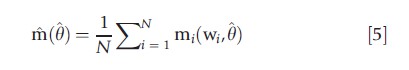
is close to zero. Under suitable assumptions, m(θ) is asymptotically normal. This leads to the chi-squared test statistic
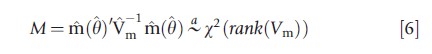
if the moment conditions eqn [4] are correct, where Vm is a consistent estimate of the asymptotic variance of m(θ). The challenge is in obtaining Vm. In some leading examples an auxiliary regression can be used, or a bootstrap can be applied.
Especially for fully parametric models there are many candidates for mi(·). Examples of this approach are White’s information matrix test to test correct specification of the likelihood function; a regression version of the chi-squared goodness of fit test; Hausman tests such as that for regressor endogeneity; and tests of over identifying restrictions in a model with endogenous regressors and an excess of instruments. Such tests are not as widely used as they might be for two reasons. First, there is usually no explicit alternative hypothesis so rejection of H0 may not provide much guidance as to how to improve the model. Second, in very large samples with actual data any test at a fixed significance level such as 0.05 is likely to reject the null hypothesis, so inevitably any model will be rejected.
Regression model diagnostics need not involve formal hypothesis tests. A range of residual diagnostic plots can provide information on model nonlinearity and observations that are outliers and have high leverage. In the linear model, a small sample correction divides the residual yi-xi`β by √1-hii, where hii is the ith diagonal entry in the hat matrix H=X(X`X)-1X. As H has rank K, the number of regressors, the average value of hii is K/n and values of hii in excess of 2K/N are viewed as having high leverage. This result extends to generalized linear models where a range of residuals have been proposed; McCullagh and Nelder (1989) provide a summary. Econometricians place less emphasis on residual analysis, compared with biostatisticians. If datasets are small then there is concern that residual analysis may lead to over fitting of the model. Besides if the dataset is large then there is a belief that residual analysis may be unnecessary as a single observation will have little impact on the analysis. Even then diagnostics may help detect data miscoding and unaccounted model nonlinearities.
For linear models, R2 is a well understood measure of goodness of fit. For nonlinear models a range of pseudo-R2 measures have been proposed. One that is easily interpreted is the squared correlation between y and ^y, though in nonlinear models this is not guaranteed to increase as regressors are added.
Model testing and diagnostics may lead to more than one candidate model. Standard hypothesis tests can be implemented for models that are nested. For nonnested models that are likelihood based, one can use a generalization of the likelihood ratio test due to Vuong (1989), or use information criteria such as Akaike’s information criteria based on fitted log-likelihood with a penalty for the number of model parameters. For nonnested models that are not likelihood based one possibility is artificial nesting that nests two candidate models in a larger model, though this approach can lead to neither model being favored.
Multiple Tests
Standard theory assumes that hypothesis tests are done once only and in isolation, whereas in practice final reported results may follow much pretesting. Ideally reported p values should control for this pretesting.
In biostatistics, it is common to include as control variables in a regression only those regressors that have p<.05. By contrast, in economics it is common to have a preselected candidate set of control regressors, such as key socioeconomic variables, and include them even if they are statistically insignificant. This avoids pretesting, at the expense of estimating larger models.
A more major related issue is that of multiple testing or multiple comparisons. Examples include testing the statistical significance of a key regressor in several subgroups of the sample (subgroup analysis); testing the statistical significance of a key regressor in regressions on a range of outcomes (such as use of a range of health services); testing the statistical significance of a key regressor interacted with various controls (interaction effects); and testing the significance of a wide range of variables on a single outcome (such as various genes on a particular form of cancer). With many such tests at standard significance levels one is clearly likely to find spurious statistical significance.
In such cases one should view the entire battery of tests as a unit. If m such tests are performed, each at statistical significance level a*, and the tests are statistically independent, then the probability of finding no statistical significance in all m tests is (1-a*)m. It follows that the probability of finding statistical significance in at least one test, called the family-wise error rate (FWER), equals a=1-(1-a*)m. To test at FWER a, each individual test should be at level a*=1-(1-a)m, called the Sidak correction. For example, if m=5 tests are conducted with FWER of a=0.05, each test should be conducted at level a*=0.01021. The simpler Bonferroni correction sets a*=a/m. The Holm correction uses a stepdown version of Bonferroni, with tests ordered by p-value from smallest to largest, so p(1) <p(2)<<p(m), and the jth test rejects if p(j)<aj*=a/(m-j+1). A stepdown version of the Sidak correction uses aj*=1-(1-a)m-j+1. These corrections are quite conservative in practice, as the multiple tests are likely to be correlated rather than independent.
Benjamini and Hochberg (1995) proposed an alternative approach to multiple testing. Recall that test size is the probability of a type I error, i.e., the probability of incorrectly rejecting the null hypothesis. For multiple tests it is natural to consider the proportion of incorrectly rejected hypotheses, the false discovery proportion (FDP), and its expectation E[FDP] called the FDR. Benjamini and Hochberg (1995) argue that it is more natural to control FDR than FEWR. They propose doing so by ordering tests by p-value from smallest to largest, so p(1)<p(2)<…<p(m), and rejecting the corresponding hypotheses H(1),…,H(k), where k is the largest j for which p(j)≤aj/m, where a is the prespecified FDR for the multiple tests. If the multiple tests are independent then the FDR equals a.
In practice tests are not independent. Farcomeni (2008) provides an extensive guide to the multiple testing literature. A recent article on estimating the FDR when tests are correlated is Schwartzman and Lin (2011). Duflo et al. (2008) provide a good discussion of practical issues that arise with multiple testing and consider the FEWR but not the FDR. White (2001) presents simulation-based methods for the related problem of testing whether the best model encountered in a specification search has a better predictive power than a benchmark model.
Bootstrap And Other Resampling Methods
Statistical inference controls for the uncertainty that the observed sample of size N is just one possible realization of a set of N possible draws from the population. This typically relies on asymptotic theory that leads to limit normal and chi-squared distributions. Alternative methods based on Monte Carlo simulation are detailed in this section.
Bootstrap
Bootstraps can be applied to a wide range of statistics. The most common use of the bootstrap is considered here, to estimate the standard error of an estimator when this is difficult to do using conventional methods.
Suppose 400 random samples from the population were available. Then 400 different estimates of θ can be obtained and the standard error of θ is simply the standard deviation of these 400 estimates. In practice, however, only one sample from the population is available. The bootstrap provides a way to generate 400 samples by resampling from the current sample. Essentially, the observed sample is viewed as the population and the bootstrap provides multiple samples from this population.
Let θ*(1),…, θ*(B) denote B estimates where, for example, B = 400. Then in the scalar case the bootstrap estimate of the variance of θ is

Where θ*= (1/B)∑Bb=1θ*(b) is the average of the B bootstrap estimates. The square root of VBoot[θ], denoted seBoot[θ], is called the bootstrap estimate of the standard error of θ. In the case of several parameters
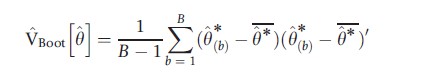
and even more generally the bootstrap may be used to estimate the variance of functions h(θ), such as marginal effects, not just θ itself.
There are several different ways that the resamples can be obtained. A key consideration is that the quantity being resampled should be independent and identically distributed (i.i.d).
The most common bootstrap for data (yi,xi) that are i.i.d. is a paired bootstrap or nonparametric bootstrap. This draws with replacement from (y1,x1),…,(yN,xN) to obtain a resample(y*1,x*1),…,(y*n,x*n) for which some observations will appear more than once, whereas others will not appear at all. Estimation using the resample yields estimate θ*. Using B similarly generated resamples yields θ*(1),…,θ*(B) . This bootstrap variance estimate is asymptotically equivalent to the White or Huber robust sandwich estimate.
If data are instead clustered with C clusters, a clustered bootstrap draws with replacement from the entire clusters, yielding a resample (y*1,X*1),…,(y*C,X*C). This bootstrap variance estimate is asymptotically equivalent to the cluster-robust sandwich estimate.
Other bootstraps place more structure on the model. A residual or design bootstrap in the linear regression model fixes the regressors and only resamples the residuals. For models with i.i.d. errors the residual bootstrap samples with replacement from u1,…,uN to yield residual resample u*1,…,u*N. Then the typical data resample is (y*1,x1),…,,(y*N,xN) where y*i=xi`β+ui*. If errors are heteroskedastic one should instead use a wild bootstrap; the simplest example is u*i=ui with probability .5 and u*i=-ui with probability .5.
For a fully parameterized model one can generate new values of the dependent variable from the fitted conditional distribution. The typical data resample is (y*1,x1),…,(y*N,xN) where y*I is a draw from F(y|xi,θ).
Whenever a bootstrap is used in applied work the seed, the initial value of the random number generator used in determining random draws, should be set to ensure replicability of results. For standard error estimation B=400 should be more than adequate.
The bootstrap can also be used for statistical inference. A Wald 95% confidence interval for scalar θ is θ±1.96 × seBoot[θ]. An asymptotically equivalent alternative interval is the percentile interval (θ*[.025], θ*[.975]), where θ*[a] is the ath quantile of θ*(1),…,θ*(B). Similarly, in testing H0:θ=0 against Ha:θ≠0 the null hypothesis may be rejected if |w|=|θ/seDoot[θ]|>1.96, or if θ<θ*[.025] or θ>θ*[.975].
Care is needed in using the bootstrap in nonstandard situations as, for example, V[θ] may not exist, even asymptotically; yet it is always possible to (erroneously) compute a bootstrap estimate of V[θ]. The bootstrap can be applied if θ is root-N consistent and asymptotically normal, and there is sufficient smoothness in the cumulative distribution functions of the data-generating process and of the statistic being bootstrapped.
Bootstrap With Asymptotic Refinement
The preceding bootstraps are asymptotically equivalent to the conventional methods of section Inference. Bootstraps with asymptotic refinement, by contrast, provide a more refined asymptotic approximation that may lead to better performance (truer test size and confidence interval coverage) in finite samples. Such bootstraps are emphasized in theory papers, but are less often implemented in applied studies.
These gains are possible if the statistic bootstrapped is asymptotically pivotal, meaning its asymptotic distribution does not depend on unknown parameters. An estimator θ that is asymptotically normal is not usually asymptotically pivotal as its distribution depends on an unknown variance parameter. However, the studentized statistic t=(θ-θ0)/sθ is asymptotically N[0,1] under H0:θ=θ0, so is asymptotically pivotal. Therefore compute t*=(θ*-θ)/sθ*, for each boot- strap resample and use quantiles of t*(1),…,t*(B) to compute critical values and p-values. Note that t* is centered around θ because the bootstrap views the sample as the population, so θ is the population value.
A 95% percentile t-confidence interval for scalar θ is (θ+t*[.025]sθ, θ+t*[.975]sθ), where t*[a] is the ath quantile of t*(1),…,t*(B). A percentile-t Wald test rejects H0:θ=θ0 against Ha:θ≠θ0 at level 0.05 if t =(θ-θ0)/sθ falls outside the interval (t*[.025], t*[.975]).
Two commonly used alternative methods to obtain confidence intervals with asymptotic refinement are the following. The bias-corrected method is a modification of the percentile method that incorporates a bootstrap estimate of the finite-sample bias in θ. For example, if the estimator is upward biased, as measured by estimated median bias, then the confidence interval is moved to the left. The bias-corrected accelerated confidence interval is an adjustment to the biascorrected method that adds an acceleration component that permits the asymptotic variance of θ to vary with θ.
Theory shows that bootstrap methods with asymptotic refinement outperform conventional asymptotic methods as N→∞. For example, a nominal 95% confidence interval with asymptotic refinement has a coverage rate of 0.95+O(N-1) rather than 0.95+O(N-1/2). This does not guarantee better performance in typical sized finite samples, but Monte Carlo studies generally confirm this to be the case. Bootstraps with refinement require a larger number of bootstraps than recommended in the previous subsection, as the critical values lie in the tails of the distribution. A common choice is B=999, with B chosen so that B+1 is divisible by the significance level 100a.
Jackknife
The jackknife is an alternative resampling scheme used for bias correction and variance estimation that predates the bootstrap.
Let θ be the original sample estimate of θ, let θ(-i) denote the parameter estimate from the sample with the ith observation deleted, i=1,..,N, and let θ=N-1∑Ni=1θ(-i) denote the average of the N jackknife estimates. The bias-corrected jackknife estimate of θ equals Nθ-(N-1)θ, the sum of the N pseudovalues θ*(-i)=Nθ-(N-1)θ(-i) that provide measures of the importance or influence of the ith observation estimating θ.
The variance of these N pseudovalues can be used to estimate V[θ], yielding the leave-one-out jackknife estimate of variance:
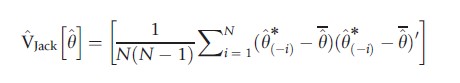
A variation replaces θ with θ.
The jackknife requires N resamples, requiring more computation than the bootstrap if N is large. The jackknife does not depend on random draws, unlike the bootstrap, so is often used to compute standard errors for published official statistics.
Permutation Tests
Permutation tests derive the distribution of a test statistic by obtaining all possible values of the test statistic under appropriate rearrangement of the data under the null hypothesis.
Consider scalar regression, so yi=β1+β2xi+ui, i=1,…,N, and Wald test of H0:β2=0 based on t=β2/sβ2. Regress each of the N! unique permutations of (y1,…,yN) on the regressors (x1,…,xN) and in each case calculate the t-statistic for H0:β2=0. Then the p-value for the original test statistic is obtained directly from the ordered distribution of the N! t-statistics.
Permutation tests are most often used to test whether two samples come from the same distribution, using the difference in means test. This is a special case of the previous example, where xi is an indicator variable equal to one for observations coming from the second sample.
Permutation methods are seldom used in multiple regression, though several different ways to extend this method have been proposed. Anderson and Robinson (2001) review these methods and argue that it is best to permute residuals obtained from estimating the model under H0, a method proposed by Freedman and Lane (1983).
Conclusion
This survey is restricted to classical inference methods for parametric models. It does not consider Bayesian inference, inference following nonparametric and semiparametric estimation, or time series complications such as models with unit roots and cointegration.
The graduate-level econometrics texts by Cameron and Trivedi (2005), Greene (2012) and Wooldridge (2010) cover especially sections Inference and Model Tests and Diagnostics; see also Jones (2000) for a survey of health econometrics models. The biostatistics literature for nonlinear models emphasizes estimators for generalized linear models; the classic reference is McCullagh and Nelder (1989). For the resampling methods in section Bootstrap and Other Resampling Methods, Efron and Tibsharani (1993) is a standard accessible reference; see also Davison and Hinkley (1997) and, for implementation, Cameron and Trivedi (2010).
References:
- Anderson, M. J. and Robinson, J. (2001). Permutation tests for linear models. Australian and New Zealand Journal of Statistics 43, 75–88.
- Andrews, D. W. K., Moreira, M. J. and Stock, J. H. (2007). Performance of conditional Wald tests in IV regression with weak instruments. Journal of Econometrics 139, 116–132.
- Benjamini, Y. and Hochberg, Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society B 57, 289–300.
- Bound, J., Jaeger, D. A. and Baker, R. M. (1995). Problems with instrumental variables estimation when the correlation between the instruments and the endogenous explanatory variable is weak. Journal of the American Statistical Association 90, 443–450.
- Cameron, A. C. and Miller, D. A. (2011). Robust inference with clustered data. In Ullah, A. and Giles, D. E. (eds.) Handbook of empirical economics and finance, pp. 1–28. Boca Raton: CRC Press.
- Cameron, A. C. and Trivedi, P. K. (2005). Microeconometrics: Methods and applications. Cambridge: Cambridge University Press.
- Cameron, A. C. and Trivedi, P. K. (2010). Microeconometrics using Stata First revised edition College Station, TX: Stata Press.
- Conley, T. G. (1999). GMM estimation with cross sectional dependence. Journal of Econometrics 92, 1–45.
- Davison, A. C. and Hinkley, D. V. (1997). Bootstrap methods and their application. Cambridge: Cambridge University Press.
- Duflo, E., Glennerster, R. and Kremer, M. (2008). Using randomization in development economics research: A toolkit. In Shultz, T. P. and Strauss, J. A. (eds.) Handbook of development economics, vol. 4, pp. 3896–3962. Amsterdam: North-Holland.
- Efron, B. and Tibsharani, J. (1993). An introduction to the bootstrap. London: Chapman and Hall.
- Farcomeni, A. (2008). A review of modern multiple hypothesis testing, with particular attention to the false discovery proportion. Statistical Methods in Medical Research 17, 347–388.
- Freedman, D. and Lane, D. (1983). A nonstochastic interpretation of reported significance levels. Journal of Business and Economic Statistics 1, 292–298.
- Greene, W. H. (2012). Econometric analysis, 7th ed. Upper Saddle River: Prentice Hall.
- Jones, A. M. (2000). Health econometrics. In Culyer, A. J. and Newhouse, J. P. (eds.) Handbook of health economics, vol. 1, pp. 265–344. Amsterdam: North-Holland.
- McCullagh, P. and Nelder, J. A. (1989). Generalized linear models, 2nd ed. London: Chapman and Hall.
- Newey, W. K. and West, K. D. (1987). A simple, positive semi-definite, heteroscedasticity and autocorrelation consistent covariance matrix. Econometrica 55, 703–708.
- Schwartzman, A. and Lin, X. (2011). The effect of correlation in false discovery rate estimation. Biometrika 98, 199–214.
- Vuong, Q. H. (1989). Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica 57, 307–333.
- White, H. (2001). A reality check for data snooping. Econometrica 68, 1097–1126.
- Wooldridge, J. M. (2003). Cluster-sample methods in applied econometrics. American Economic Review 93, 133–138.
- Wooldridge, J. M. (2010). Econometric analysis of cross section and panel data, 2nd ed. Cambridge, MA: MIT Press.