The distributions of both healthcare expenditures and utilization share a number of characteristics that make their analysis more complicated than conventional economics outcomes; see also Cameron and Trivedi (2013). This article will focus on the analogous issues for costs and expenditures on healthcare. The most salient of these characteristics for many health economics applications are as follows: (1) a substantial part of the population will have no costs or expenditures during the period of observation; (2) among those with any expenditure, the amount is typically dramatically skewed right; and (3) not all parts of the distribution respond the same way to covariates. Even in clinical populations based on being treated for a specific health condition, the last two characteristics are still important. It is not uncommon to find that the top 1% of the population consumes nearly a fifth to a fourth of total health resources, and the top 10% nearly half of the total. Some types of expenditures are even more skewed with the top tenth of the distribution accounting for half or more of all healthcare expenditures, such as inpatient or mental health. These upper centiles or deciles may respond differently, such as being less elastic in their response to out-of-pocket price or income. In the Health Insurance Experiment (HIE), the upper decile was composed mostly of inpatient users, who were less responsive to insurance coverage than outpatient-only users (Duan et al., 1983; Manning et al., 1987).
Analysts have often found that the use of the least squares estimator with such data often leads to analytical problems from highly influential outliers – catastrophic cases, or chronic care patients with many visits and substantial pharmacy costs unless the sample size is sufficiently large so that there are a substantial number of such cases. For example, see the works on risk adjustment using a large fraction of the US Medicare claims files for risk adjustment. As the sample size becomes very large, the same concern does not remain, that the results will be driven by a small number of observations with catastrophic expenditures having undue influence.
Without the luxury of enormous data files, there is often the temptation to remove these extreme cases; removing or trimming or winsorizing such cases will reduce the influence of the extreme cases but will also introduce bias because catastrophic cases do occur in health and do consume real resources. Because of these issues, analysts often find that results are not replicable across alternative samples drawn from the same population. Least squares estimation under these circumstances is inefficient and in some cases biased, especially if zeroes are prevalent. Even when the estimates are unbiased, the inferences are biased because the underlying heteroscedasticity implicit in a model with a strictly nonnegative dependent variable is ignored. The inefficiency in the estimates and bias in the inference statistics for ordinary least squares (OLS) results arise from the property that the variability in costs is often an increasing function of the mean or some other function of the covariates x.
Health economists and econometricians have adapted various methods to deal with different outcomes and issues. The largest division is between count estimators to address the integer nature of MD visits and hospital admissions, compared to estimation approaches designed for continuous positive outcomes such as expenditures; survival approaches have been used, but are less common than the major splits of counts versus continuous. A cross-cutting issue is how to address the mass of observations at zero in either type of outcome, but the specific solutions differ both by the type of data on the outcome and by the underlying research question. In the case of count data, the concerns may include the mean response or marginal and incremental effects, or the response probability that the specific values of the counts respond in a particular way – does a change in the dental insurance coverage for prophylaxis change the probability that a patient has two such visits per year?
In the case of the limited dependent variable for expenditures, the issues are often the likelihood of any use and the overall mean response or some function of these such as the marginal and incremental effect. In both cases, the skewed nature of the outcome variables may make the results sensitive to influential outliers unless suitable methods are employed.
This article will focus on the health costs and expenditure case for individuals.
With data from either a general population or a population of users, it is not uncommon for cases in the top 1% of the distribution to have values that are nine times the sample mean, have studentized residuals that are beyond the +4σ range, and maybe in double digits for the far right tail of the distribution, especially for expenditures. If such values are coupled with deviant values for the covariates, then they may have tremendous influence on the estimates. Because cost and expenditure data are so skewed right, there are no countervailing large residuals in the left tail. The consequence is that in small and moderate-sized samples, a single case can have tremendous influence on the estimates; as the sample size N increases, this issue of influence is diminished, especially with very large data sets, such as those used in estimating risk adjusters for the US Medicare program. The one notable exception occurs when one of the rate cells is relatively rare; see comments in Mihaylova et al. (2011). In the HIE, one single observation accounted for approximately 17% of the mean for that insurance plan.
The issues are different for very large data sets. As the sample size N increases, this issue of influence to skewness diminishes. The major modeling issue is getting the functional form to reflect the nonlinear nature of the response, an issue that applies to data sets of all sizes.
In what follows, first, a brief introduction to alternative approaches is provided for these types of healthcare or medical-care expenditures (or continuous positive outcomes). Then questions about the treatment of the zero mass and skewness are addressed. There are some comments on methods for assessing differential responses in different parts of the distribution. Except where noted, the discussion applies to observations for fixed-size intervals of observations, rather than unequal-sized intervals; the latter can be addressed with formal offsets in some models.
Healthcare Expenditures
In what follows, a summary is provided of a number of issues that are of econometric and statistical concern in the modeling of healthcare expenditures. Jones (2011), Mihaylova et al. (2011), and Mullahy (2009) provided reviews of the modeling of healthcare expenditures and continuous outcomes with a more detailed discussion related to much of what is presented here.
Addressing The Zeroes Issue
Healthcare expenditures are nonnegative, often with many zeroes for the period of observation. One of the first issues is how to address the zeroes in the econometric modeling of the mean conditional on the covariates or of marginal effects when the focus of the analysis is on a general population rather than a clinical population of healthcare users. One approach has been to break down the distribution into two or more parts using the following rule:
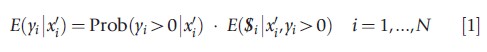
The classes of two-part estimators provide different approaches to each part, with the two terms on the right side typically modeled separately because of the conditional independence of the second part (Cragg, 1967; Duan et al., 1983). This type of estimators have been extended to include multipart models as well to address additional complication, such as differential response in the right tail, largely associated with inpatient care in the HIE (Duan et al., 1983; Manning et al., 1987). The analytical issues for both two-part and multipart models involve choices of the estimation approach for any expenditure and for the level of expenditure that are appropriate for the data at hand.
There is an alternative approach for the case where the concern is the mean response (conditional on a set of characteristics). That alternative involves a one-part part or single-equation, nonlinear model to obtain consistent estimates of E(y|x), where the underlying explanatory variables are the same as those in the two-part models in equation 1 above. There is no necessity that the functional form of the response is the same as that for the second part of eqn [1]. For two-part models, see Duan et al. (1983), Blough et al. (1999), and various papers by X. H. Zhou. For single or one-part model, see Mullahy (1998) and Buntin and Zaslavksy (2004). There appear to be two unresolved issues in the debate over one-versus two-part models. The first is how large a fraction of the observations should be zeroes to make a difference, if any, in terms of bias or efficiency. The second is to what extent is this debate about the choice of the number of parts, rather than about how complicated the covariate specification should be to fit the actual distribution across the range of predictions in one versus two-part models? Would a one-part model with additional covariates be able to capture curvature in the data to be equivalent to a two-part model?
There is a third, less common approach that builds on bivariate normal methods for two-part models, rather than the conditioning argument behind eqn [1], that are sometimes referred to as adjusted or generalized Tobit models or Heckit models. There is mixed evidence on how well these alternative estimators behave if there are no identifying restrictions across equations, which is the most common situation in health, unlike in labor economics. There are two common misconceptions in this debate. The first is that two-part models are nested within the bivariate normal alternatives; they are not. The second is that two-part models assume no correlation between any use and level of use; there are counterexamples in the literature.
All of the models considered here may be sensitive to influential outliers. The sensitivity to extreme cases is a natural byproduct of the skewness in the data. If expenditures were to be analyzed by a standard OLS model of the form yi=x`iβ+εi where yi is the cost or expenditure on the raw scale (dollars, Euros, or pounds) for observation i, x`i is a row vector of observed characteristics, and β is a column vector of coefficients to be estimated. Then the effect of an individual observation i on the estimate of β can be characterized by Cook’s distance or the DFITS measure. Both measures depend on how extreme the observation is in terms of both the covariate values and the residual squared. These two diagnostics can be extended to nonlinear models as well as for least squares, as well as other tests of model checking such as Pregibon’s Link Test or can be extended to include more complicated nonlinearity (as in Ramsey’s RESET test), or less parametrically using a modified version of the Hosmer–Lemeshow test.
Addressing Skewed Positive Or Overall Expenditures Or Overall Nonnegative Expenditures
There are several approaches to dealing with such data: do nothing beyond OLS, use a Box–Cox transformation of the dependent variable, use one of the generalized linear models (GLMs) appropriate for continuous outcomes, use one of the three- and four-parameter distributions, or use a flexible and robust approximations to the underlying distribution. The consequence of the all-too-common alternative of ignoring the skewed data with a least squares approach is that the results are (1) sensitive to the skewness in the dependent variable, especially if the data set is of small or moderate size (such as the Medical Expenditure Panel Survey), and some of the characteristics are rare, and (2) the inference statistics are biased given the inherent heteroscedasticity in the data has not been captured in the estimation.
Box–Cox Models
One alternative is to transform the dependent variable by the natural logarithm or a power transformation to eliminate the skewness in the error; transformations may also be used to achieve a model that is linear in the parameters (as in the Cobb–Douglas production function) or to stabilize the variance of the equation estimated (as in the square root transformation for count data or the inverse sine root transform for proportions). Some of these transformations are special cases of the Box–Cox transformation, but some are less reliant on parametric distributional assumptions. Specifically, the Box–Cox models consider transformed equations f(y) if y is positive of the form
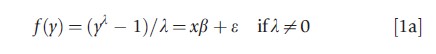
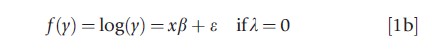
It is often assumed that e is either symmetric or normally distributed. The model can be estimated either by maximum likelihood estimation (MLE) or by the use of least squares for suitable values of λ. There are also two-parameter versions of the Box–Cox model that allow explicitly for the mass of observations at zeroes, but these do not always provide consistent estimates of the mean outcome, conditional on the covariates.
The advantage of the power transformation if λ<1 for data that are skewed to the right is that it pulls in the right tail of the distribution faster than it does in the middle or the left tail. As λ decreases toward zero, the error term in the estimated equation should become more symmetric, reducing the influence of the extreme cases in the right tail of the distribution. However, too low a values of λ (such as the log, when 0<λ<1 would be more suitable) may lead to overcorrection in the sense that it would convert a right-skewed distribution into a left-skewed one after the transformation. The log transformation is not always the optimal choice for right-skewed data.
The problem with the log and Box–Cox approaches is that one is often not interested in the transformed scale per se – the government does not spend log dollars or log Euros. Rather, one is actually interested in the raw scale of expenditures y and predictions or marginal effects in dollars or Euros (in E(y9x) more generally). This leads to concerns about the retransformation of the results from the scale of estimation (e.g., the log or the λth power) to the scale of interest (e.g., raw or actual dollars or Euros). Because of the nonlinear nature of the log and Box–Cox transformations, the transformation cannot be simply inverted to obtain unbiased estimates of the E(y|x) because E(f(y|x))≠ f(E(y|x)), where f(y) is the transformation. This is the retransformation problem discussed by Duan (1983), Duan et al. (1983), Manning (1998), Mullahy (1998), and Blough et al. (1999).
The difference between the two is easy to see in the case of OLS on ln(y) if the error term is log normally distributed. OLS generates unbiased estimates of E(ln(yi|xi))=x`iβ if E(X’ε)=0. However, the term E(exp(x`iβ)) yields an estimate of the geometric mean, not the arithmetic mean of the response function. The arithmetic mean is E(yi|xi )=exp(x`iβ+0.5σ2ε) if ε is i.i.d. and normally distributed, and E(yi|xi)=exp(x`iβ+0.5σ2(x)) if normally distributed and heteroscedastic in x (Manning, 1998). If the error is not normally distributed, then the estimates x`iβ may be consistent, but one can apply Duan’s (1983) multiplicative smearing factor in the homoscedastic case to provide a consistent estimate of E(exp(εi)), or its analog in the heteroscedastic case to obtain the mean response.
The goal of most analyses is some statement about how the mean or some function of the mean of y, such as the marginal effect on the raw scale, changes with x. In general, the expectation of y depends on the variance and heteroscedasticity on the log scale and on how higher order terms depend on the covariates. If the variable of interest xj is not discrete, then the slope of the expected value with respect to the jth covariate is given by

It is the first derivative in eqn [2] that should be used in the calculation of the elasticity of the mean response or the average marginal effect, rather than either of the other two in the case of log scale heteroscedasticity if the log-scale error is normally distributed. The last one applies only if R2=100% on the log scale.
In the nonnormal case or for values of λ other than zero, the derivative will depend on the power transform λ, the nature of the distribution in the absence of the additional complication of heteroscedasticity:

where F(ε) is the cdf for the error term.
In the square root case where √yi=x`iβ+ε with possible heteroscedasticity, the scale of interest relationship is E(yi|xi)=(x`iβ)2+σ2ε(xi). Here the retransformation factor is additive. The retransformation factor will be multiplicative only in the case of λ=0 and will be moot if λ=1.
There are a number of technical issues that arise with Box–Cox models. One of these is how to deal with observations where y=0. Second, the estimates of the power transform are sensitive to extreme outliers in ε. In practice, it may be difficult to tell the effect of an influential outlier from skewness in the dependent measure that is not associated with the covariates. Third, if λ is not known a priori, then all of the inferences should reflect that β’s, λ, and σ are estimated in calculating inference statistics for eqns [2] and [3], not just the β’s.
Generalized Linear Models
A second alternative to a least squares linear model using some f(y) directly is to model the f(E(y) directly and deal with the skewed expenditure data (with or without the zeroes) by addressing the property that the variance function is often an increasing function of the mean. This can be done by using some iteratively reweighted least squares alternative or the GLMs for continuous outcomes (such as gamma regression) estimated with quasi-maximum likelihood methods. In the GLM case, the analyst specifies a link function between the linear model x’β and the mean, so that g(E(y|x))=x’β, and a variance function v(y|x) that characterizes the nature of the relationship between the mean and the variance on the raw scale. The v(y|x) function is assumed to be a function of the mean, not of individual covariates in x directly. The correct specification of the variance function results in more efficient estimators and may correspond to an underlying distribution of the outcome measure. If the distribution is from the exponential family, then the estimation can be done by quasimaximum likelihood methods. Although one can perform an MLE using the specific distributions, the conventional GLM is more robust in the sense it does not assume the distribution beyond the first and second moments. So, for the gamma GLM, only the gamma variance (the variance function increases as the square of the mean function) is assumed and not the full gamma distribution.
If the link function is misspecified, then the estimates will provide a biased estimate of the response. Much of the work to date on healthcare expenditures has used a log link: ln (E(yi|xi)=x`iδ; I use δ has been used for the index function in the log link GLM to avoid possible confusion with β from the ln(y) model. If the ln(y) error is homoscedastic, they have the same expectation, except for the intercept where δ0 corresponds in expectation to β0+ln[E(exp(εi))]. However, some papers have also used power transformations, such as the square root. Just because the log transformation is often used in transformed y models, there is no reason to assume the same for the GLM or to use λ=0 for all cases that are skewed right. In the transformed y models, the log (or any other Box–Cox transformation) is designed to achieve symmetry in the error. In the GLM case, the goal is to find a function of a linear index (say x`δ, which provides a consistent estimate of E(y|x) over the range of x`δ and the major covariates in x`δ. This difference between least squares on transformed y and GLMs with power or log links is very important to understand, and has been a common source of confusion between log/ Box–Cox methods and GLM alternatives.
Since the late 1990s, the most commonly used distribution for GLM applied to positive healthcare cost or expenditure data has been the gamma. This is appealing working assumption for the distribution function because the standard deviation under the gamma is proportional to the mean, a property often but not always exhibited by healthcare cost data. However, this is only one of several cases where the standard deviation or the variance is a power of the mean function. If the variance is not a function of the mean, then a Gaussian assumption may be used (Mullahy, 1998; Wooldridge, 1992). If the variance is proportional to the mean, then the Poisson may be more appropriate. If the standard deviation is proportional to the cube of the mean, then the inverse Gaussian is an alternative. Other applications could employ powers of the variance as in Blough et al. (1999) and Basu and Rathouz (2005) approach (see below).
As long as the link function and the index function of the covariates x`iδ are correctly specified, the GLM provides consistent estimates. The wrong mean–variance relationship or the wrong distribution function can potentially lead to substantial efficiency losses. For Box–Cox models, there may be bias if there is heteroscedasticity and efficiency loss if the underlying error is not normal. Manning and Mullahy (2001) provide a fuller discussion and simulation results that illustrate the trade-offs involved among log(y) and GLM with log links. One implication of their work is that there is no one estimation approach that is ideal or even a close second best approach for all examples. The best estimation approach depends on the application at hand and its underlying datagenerating process.
Extended GLM Methods
There is a hybrid of the Box–Cox type of model and the GLM. Basu and Rathouz (2005) describe an extended estimating equation (EEE) algorithm that allows one to use the data to estimate both the link function from the power family via the Box–Cox link for the mean function and the power family relationship between the mean and the variance functions.

This approach is more general than the two preceding alternatives and avoids the issues that arise in the common practice of using only a discrete set of GLM alternatives for the link and mean–variance relationship. In both the Box–Cox model and the GLM, the choice of the wrong transform of y or link for E(y|x) can lead to biased estimates. In the GLM, only using integer powers for the mean–variance relationship can lead to a substantial loss of efficiency. Further, the results for inference statistics will reflect the uncertainty in the estimates of λ and θ2 , thus avoiding the corresponding issue and debate in statistics over the Box–Cox transformation of y.
Other Parametric Approaches
Manning et al. (2005) propose using an exponential conditional mean regression based on the three-parameter generalized gamma distribution that could be estimated by maximum likelihood. The generalized gamma model includes the gamma, Weibull, and exponential distributions with log link, as well as models for ln(y) with normal errors. This approach also provides a robust alternative to either the GLM with log link or the OLS on ln(y) when those two alternatives do not apply, assuming that the mean is truly an exponential function of x`β. The generalized gamma is a more precise alternative than the GLM when the distribution is more skewed than is implicit in the GLM case. However, the generalized gamma is susceptible to bias in the presence of certain forms of heteroscedasticity on the log scale. Manning et al. (2005) propose a modification of the model that corrects for this by allowing for two index functions, one for the ln(σ) term and the other for the log-scale mean.
There is some preliminary interest in four-parameter distributions, such as the generalized betas of the second kind because they allow for better fit to the actual distribution of positive expenditures, as well as have several of the other alternatives as special cases if the link is log or there is a proportional response. There is related work by the distribution of income. The five-parameter distribution has not been employed to the best of the author’s knowledge. Nevertheless, the generalized gamma and the four- and five-parameter versions of the generalized beta permit an explicit allowance for skewness that is not always fully captured in simpler two-parameter distributions such as the Box–Cox/log normal or the GLM with its focus on the first two moments. Jones (2011) reports results from a parametric model in the generalized beta of the second class. Although that model allows only one of the parameters to be a function of covariates, Jones has work allowing two or more parameters being a function of covariates. This work would be more general and flexible than either the GLM (with log link) or the generalized gamma, because these are limiting cases or more restrictive variants of the generalized beta of the second kind (GB2). That statistical distribution has a richer parameterization that allows the parameters to depend on patient or other characteristics.
Differential Responsiveness
In their common formulations, the previous methods do not allow for heterogeneity in the healthcare responses to covariates over the population, by service, over the distribution of expenditures, or by allowing for latent groups. Quantile methods could be used to allow for differential responses, if allowances are made for ties in the zero spenders. The multipart models, especially the four-part model used in the HIE (Duan et al., 1983) allow for inpatient users to have a different response to covariates; the four-part model is also a mixture model with known or observable separation among subgroups and differs from the latent class models more often used for count data. Finite mixture models with unobserved or unknown separation can be used to approximate an arbitrary distribution and to allow for some heterogeneity in response, given the number of latent classes included.
Less-Parametric Approaches
Gilleskie and Mroz (2004) have suggested that one can use a series of conditional models to address the skewed nature of healthcare expenditures and the zeroes problems together. They suggest a conditional density estimator (CDE) that breaks the dependent variable (healthcare expenditures) into J different segments, modeling the probability p of being in a specific segment j as a function of the covariates x’s as a polynomial function f of the covariates x, and then using subsample means of y within each of those J segments. The basic approach takes advantage of the way conditional distributions work, namely, that E(y)=E(y|z)·E(z). In this case, the expected value of y, given the observed characteristics of the population is
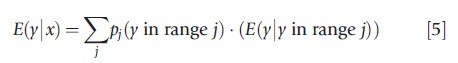
The overall response E(y|x) for person i over the j ranges is given by

where j is an index for segments and x’s are polynomials in the underlying independent variables. Gilleskie and Mroz propose a very specific form for the probability functions pj(x`iaj), but one can use a more general approach than they used. By breaking the dependent variables into bounded values (except for the last segment), they avoid some of the issues of robustness to skewness in y because the values of y in a specified range are not as long tailed as the whole distribution of y. By using a polynomial in the underlying covariates, they allow for a nonlinear response to the individual characteristics.
Given the complexity of the model in eqns [4] and [5], the effects of covariates are assessed using a marginal or incremental effects approach just as in the multipart models.
They find that the model performs well in a range of simulated conditions. Also, they are able to obtain well-behaved results with data drawn from the HIE. One of two remaining issues is how big the intervals should be, especially given the substantial part of the overall expenditures that are in the last (open) interval. The other is how to model means of intervals if the mean conditional on being in an interval depends on covariates.
Assessing Model Fit
The literature provides a number of tests that can be applied to most of these models to assess the quality of the fit whether the model is based on single-equation methods (with or without the zeroes), two-part or multipart models, or GLM and extended GLM. Some of the omnibus fits of test are primarily done on the scale of estimation; they include Pregibon’s Link Test and Ramsey’s RESET test. The Pearson correlation test between the raw-scale residual and the rawscale prediction, and the modified Hosmer–Lemeshow test, can be performed on the raw scale, which is often the scale of interest. Buntin and Zaslavsky (2004) provide discussions of a number of these, plus others that are often used in the risk adjustment literature.
Generally, the two-part and multipart models are more difficult to assess the overall fit because there is no established analog of Pregibon’s Link or Ramsey’s RESET test for multipart models. For this and the CDE class of models, model assessment is limited to Pearson and modified Hosmer–Lemeshow for in-sample assessment, and the usual cross-sample validation approaches including simple split sample or k-fold methods. There are other extensions of split sample cross-validation approaches that can be used on the scale of estimation, including the type of two-parameter more parsimonious work by Copas (1997). In health services research, there is also a set of crossvalidation tests that have been called Copas tests but differ in that the estimates from the first split sample are predicted to the test or validation sample on the raw scale, sometimes called the scale of interest. There the test is whether the regression of the raw scale version of the dependent variable to the test but on the raw scale is a straight line through the origin with slope 1; see Veazie et al. (2003) and Basu et al. (2006).
Quantile Approaches
With the exception of the Gilleskie and Mroz (2004) approach discussed earlier, the approaches have been largely parametric. Often these approaches have assumed that there is limited heterogeneity in response over the distribution of expenditures (inpatient vs. outpatient, or across a small number of latent classes). Another approach is to employ quantile regression methods that allow the responses to differ across the distribution of expenditures, conditional on a set of covariates based on the quantile methods reviewed in Koenker (2005).
Note that these provide a more flexible approach to modeling the response because the responses are not forced to be parallel on the scale of estimation. For example, if the inpatient and outpatient responses are different, then that can be addressed with separate models for different services or by a multipart model. But if the catastrophic inpatient cases had a different response to income and price, then the simpler models could fail to be parallel in the right tail, where so much of the total resource cost and expenditure are.
This article will not address those quantile approaches in detail.
Strengths And Weaknesses
There have been a substantial number of papers of econometric and statistical models for modeling healthcare costs and expenditures as a function of patient characteristics of interest. Many of these deal with the whole distribution, especially the substantial fraction of the cases that have zero expenditure. Many of these papers involve comparisons for alternative models with the evaluation largely limited to how well specific models do for a specific data set. One of the concerns about such studies is their generalizability to other populations or to other types of healthcare expenditures. A second concern is that the performance in a specific application may reflect overfitting of badly skewed data, because many of the papers use within-estimation sample methods to evaluate the relative performance of the alternatives.
Manning and Mullahy (2001) report simulated comparisons of several exponential conditional mean models under a range of different data-generating mechanisms. These include the use of OLS on ln(y), various types of GLMs with log links (Gaussian, Poisson, and gamma). In each case, the true response was exponential conditional mean E(y|x)= exp(xβ). They examined a number of data-generating mechanisms that lead to varying degrees of skewness, heteroscedasticity on the log scale, and even heavy-tailed distributions for ln(y). In the absence of heteroscedasticity on the log scale, they found that both the OLS on ln(y) and GLM with log link models provided consistent estimates of E(y|x). But if the true model was linear on the log scale with an additive error term that was heteroscedastic in x, the log OLS provided biased estimates of E(y|x) without suitable retransformation.
Although the GLM were always consistent, the choice of variance function assumption had substantial impact on the efficiency of the estimation, especially when compared with the results based on OLS on ln(y). Further, the loss of efficiency relative to OLS on ln(y) increased as the data became more skewed or became heavy tailed on the log scale.
Because of the potential for bias from OLS on ln(y) and of efficiency losses from the GLM with log link models when the log-scale error variances are large or the log-scale error is heavy tailed, they propose an approach for determining which estimation approach is better for a specific data set.
Basu and Rathouz (2005) also simulate the behavior of various GLM versus their proposed EEE extension of the GLM. They find evidence of bias and inefficiency when the incorrect power transformations are used for either or both of the link and the variance functions. But they do not examine the traditional Box–Cox estimator.
Except for Basu and Rathouz (2005) and subsequently Basu et al. (2006), there is little in the literature outside the exponential conditional mean that is not specific to a particular data set or health condition. But there is no reason why other link or Box–Cox style transformations of the dependent variable could not be used or seriously considered. More flexible alternatives could be used and then the results reported as incremental or marginal effects.
With data as skewed or with as many zeroes as healthcare data have, there is always a concern about overfitting. Traditional split-sample or cross-validation tests, or the more parsimonious Copas’s (1997) tests on the scale of estimation can be employed to assess overfitting in the narrower sense of the term. But there is also a concern about how well the model fits on the scale of ultimate interest, especially if payment/risk adjustment issues are involved. Some of these have extended to split-sample, out-of-sample tests, and to test/validation sample methods on the scale of interest by Veazie et al. (2003) and Basu et al. (2006). These provide more confidence in the results than ones conducted on the statistical scale-of-estimation, as Copas and others have done; see Hill and Miller (2010) for a recent example of a scale-of-interest comparison.
Conclusions
Because of the very skewed nature of healthcare costs and expenditures, analysis based on simple regressions of costs or expenditures are not robust in data sets with the number of observations encountered by most analysts. The focus in most applications is on finding more robust estimates of the mean response than simple OLS, conditional on the covariates, or the marginal and incremental effects of particular policies or treatments. The literature offers a number of alternative estimation strategies for expenditures. These include both single and multipart models using a range of options to deal with skewness in general or in the positive cases: Box–Cox transformations (especially the log) of the dependent variable, and GLMs, and a less restrictive version of the GLM-type approach (the extended GLM or EEE), a broader class of distributional assumptions (the generalized gamma and the generalized beta), a discrete and less parametric approximation, have been suggested as alternative estimators.
At this point, it does not appear that any specific approach dominates the modeling of the data with continuous outcomes beyond the nonuser subset. Instead, it appears that econometric model needs to be able to address the research question and to match the characteristics of the data if the estimate is to be relatively efficient, with little bias, and to pass the Cox test. To paraphrase Cox and Draper, all models are wrong, but some are useful. That is, some econometric methods provide better approximations than others.
Acknowledgments
This article has benefited from the support of the Harris School of Public Policy Studies at the University of Chicago and the thoughtful comments from colleagues and from the associate editors Anirban Basu and John Mullahy.
References:
- Basu, A., Arondekar, B. V. and Rathouz., P. J. (2006). Scale of interest versus scale of estimation: Comparing alternative estimators for the incremental costs of comorbidity. Health Economics 15(10), 1091–1107.
- Basu, A. and Rathouz, P. (2005). Using flexible link and variance models. Biostatistics 6, 93–109.
- Blough, D. K., Madden, C. W. and Hornbrook., M. C. (1999). Modeling risk using generalized linear models. Journal of Health Economics 18, 153–171.
- Buntin, M. B. and Zaslavsky, A. M. (2004). Too much ado about two-part models and transformation? Comparing methods of modeling Medicare expenditures. Journal of Health Economics 23, 525–542.
- Cameron, A. C. and Trivedi, P. K. (2013). Regression analysis of count data (2nd edition). Cambridge: Cambridge University Press.
- Copas, J. B. (1997). Using regression models for prediction: Shrinkage and regression to the mean. Statistical Methods in Medical Research 6(2), 167–183.
- Cragg, J. (1967). Some statistical models for limited dependent variables with application to the demand for durable goods. Econometrica 35, 829–844.
- Duan, N. (1983). Smearing estimate: A nonparametric retransformation method. Journal of the American Statistical Association 78, 605–610.
- Duan, N., Manning, W. G., Morris, C. N. and Newhouse, J. P. (1983). A comparison of alternative models for the demand for medical care. Journal of Business and Economic Statistics 1, 115–126.
- Gilleskie, D. B. and Mroz, T. A. (2004). A flexible approach for estimating the effects of covariates on health expenditures. Journal of Health Economics 23, 391–418.
- Hill, S. C. and Miller, G. E. (2010). Health expenditure estimation and functional form: Applications of the generalized gamma and extended estimating equations models. Health Economics 19(5), 608–627.
- Jones, A. M. (2011). Models for health care. In Clements, M. and Hendry, D. (eds.) Handbook of economic forecasting, pp. 625–634. Oxford: Oxford University Press.
- Koenker, R. (2005). Quantile regression (Econometric Society Monographs). Cambridge: Cambridge University Press.
- Manning, W. G. (1998). The logged dependent variable, heteroscedasticity, and the retransformation problem. Journal of Health Economics 17, 283–295.
- Manning, W. G., Basu, A. and Mullahy, J. (2005). Generalized modeling approaches to risk adjustment of skewed outcomes data. Journal of Health Economics 24(3), 465–488.
- Manning, W. G. and Mullahy, J. (2001). Estimating log models: To transform or not to transform? Journal of Health Economics 20(4), 461–494.
- Manning, W. G., Newhouse, J. P., Duan, N., et al. (1987). Health insurance and the demand for medical care: Evidence from a randomized experiment. American Economic Review 77(3), 251–277.
- Mihaylova, B., Briggs, A., O’Hagan, A. and Thompson, S. G. (2011). Review of statistical methods for analyzing healthcare resources and costs. Health Economics 20(8), 897–916.
- Mullahy, J. (1998). Much ado about two: Reconsidering retransformation and the two-part model in health econometrics. Journal of Health Economics 17, 247–281.
- Mullahy, J. (2009). Econometric modeling of health care costs and expenditures: A survey of analytical issues and related policy considerations. Medical Care 47(7 supplement 1), S104–S108.
- Veazie, P. J., Manning, W. G. and Kane, R. L. (2003). Improving risk adjustment for Medicare capitated reimbursement using nonlinear models. Medical Care 41(6), 741–752.
- Wooldridge, J. M. (1992). Some alternatives to the Box–Cox regression model. International Economic Review 33, 935–955.
- Basu, A. (2005). Extended generalized linear models: Simultaneous estimation of flexible link and variance functions. The Stata Journal 5(4), 501–516.