Bayesian econometrics has become an increasingly popular paradigm for the fitting of economic models, since the early 1990s. Although Bayesian efforts in economics existed well before this time – perhaps originating in our specific discipline with the pioneering work of Zellner in the early 1970s – Bayesian applied work before 1990 was relatively scarce and often resorted to approximate or asymptotic posterior analysis in order to make the approach operational.
The rather dramatic upswing in popularity that occurred in the 1990s seemingly, and perhaps surprisingly to many previously embroiled in the Bayes/frequentist debate, had little to do with ideology or a conversion of the masses to the tenets of Bayesian theory but instead was derived from a simulation-based ‘revolution’ that greatly facilitated Bayesian computation. Although, in principle, posterior distributions could always be obtained on the combination of prior and likelihood, numerical characterization of the posterior and its specific properties offered a daunting – and often insurmountable – computational challenge.
The purpose of this article is to review, in very general terms, two popular simulation-based algorithms that have greatly simplified the practice of Bayesian econometrics: the Gibbs sampling and the Metropolis–Hastings (M–H) algorithms, and to illustrate how these can be used to fit various microeconometric models commonly employed in health economics. The article reviews the basic procedures for implementing these algorithms, discusses strategies for diagnosing their convergence (or nonconvergence) and, finally, illustrates their application in various examples involving wages and their relationship to the Body Mass Index (BMI).
The outline of the article is as follows. The following section reviews the general approach to Bayesian estimation and inference and then provides details of both the Gibbs sampling and M–H algorithms in a representative setting. The authors then apply the Gibbs sampling algorithm in a linear regression model and review issues of convergence diagnostics and posterior prediction within that context. The Section Bayesian Inference in Latent Variable Models extends these ideas to nonlinear settings, thereby providing a generic representation that encompasses a variety of discrete choice models widely used in health applications. This article concludes with a brief summary.
How It Works
To begin, by consider a model M that yields a parametric likelihood function L(y; y). The reader with no previous exposure to Bayes will likely find this portion of the empirical exercise familiar: Distributional assumptions on unobserved components of the model induce a sampling distribution for the data y, denoted as pðy9yÞ. Common examples include the assumption of normally distributed errors in linear regression, yielding the classical normal linear regression model (LRM), or extreme value-distributed errors in the context of a binary choice problem, leading to the logit. Regarded as a function of y given the observed data y, this defines the likelihood function.
A non-Bayesian or frequentist econometrician who is willing to go so far as to impose enough model structure to define a likelihood stops at this point, often proceeding with well-established tools for point estimation and known asymptotic approximations for inference. The Bayesian, however, continues beyond the specification of a likelihood and adds to it a prior, denoted as p(y), describing their beliefs regarding values of the parameters before having witnessed the data. In some cases, the adopted prior may be ‘informative,’ constructed from results obtained from past studies or information offered to the researcher by an expert. What is commonly done in practice, however, is to employ a prior that is proper (i.e., it integrates to unity) yet suitably ‘diffuse’ or ‘noninformative’ in the sense that the data information will typically overwhelm whatever information is insinuated through the prior.
It is at this stage of adopting a prior that the frequentist often becomes uncomfortable, fearing that the analysis is no longer objective and that the Bayesian practitioner could and may have derived the results they want simply by choosing the prior accordingly. Although commenting on issues of prior sensitivity falls a little outside the very general goals of this article, such questions will inevitably be posed to any Bayesian practitioner. In light of this, it seems useful to at least make a few brief points on this front, both as a means to motivate the Bayesian approach and also to offer the novice Bayesian a few possible responses to these kinds of queries.
First, it is useful to point out that in smooth, finite-dimensional models – such as all those considered here – the priors employed typically have little effect on posterior results with even moderate data. Although prior sensitivity is certainly a concern, the issue is often overblown and raised by those with an inherent distrust of Bayesian methods and, often, little knowledge of their operation. The influence of the prior is, however, of first-order importance in Bayesian model selection and comparison – an issue which is not addressed in detail here but is discussed in the References: provided at the conclusion of this article.
Second, to say that frequentist econometrics is prior free and clearly differentiated from the Bayesian approach by its lack of subjectivity is simply incorrect. The very process of model/variable selection is inevitably personal and subjective: Imagine, for example, two different researchers locked in separate rooms, each in possession of a data set such as the National Longitudinal Survey of Youth or National Health and Nutrition Examination Survey and seeking to use it to answer the same economic question. It does not seem controversial to conclude that these two researchers will almost surely arrive at different final models with resulting summary point estimates. The fact that ordinary least squares (OLS) or some other ‘objective’ estimator was used in the estimation of parameters in the final models simply masked the appearance of prior information that was used at earlier parts of the modeling process. One researcher will have deemed one subset of covariates as relevant and worthy of potential inclusion and further consideration, whereas the other, via his or her own beliefs and decision making, will likely focus on a different set of explanatory variables. These types of judgments are simply prior beliefs at work, and these types of priors that sculpt the classes of models to be entertained are, in fact, more restrictive than priors over parameters that the Bayesian employs, because the data can at least revise the latter type of belief, whereas no amount of data can revise the former.
Finally, there are a variety of numerical strategies for assessing the sensitivity of posterior estimation results with respect to the prior, and care regarding the prior and its influence should be a component of any serious Bayesian endeavor. Given the goals of this article, these methods cannot be discussed in detail, but the reader is advised to refer again to the References: at the conclusion of this article.
Bayesian Computation
Now turn to the practical issue of Bayesian computation. Given the likelihood L(θ; y) and prior p(θ), the joint posterior distribution, denoted as p(θ|y), is obtained via Bayes’ Theorem as:

The posterior distribution in eqn [1] summarizes beliefs regarding θ after having combined the prior and likelihood and represents the output of any Bayesian analysis. When θ is univariate or bivariate, this output can be summarized by simply plotting the prior times likelihood in the numerator of eqn [1] over different values of θ, thus providing the analyst with a sense of the overall shape of the joint posterior. In most cases, however, p(θ|y) is high dimensional, rendering this type of visual analysis practically infeasible.
In models of even moderate complexity, moments or specific features of eqn [1] cannot be directly calculated, as the denominator – the normalizing constant of the posterior – cannot be determined analytically. Moreover, even if this normalizing constant were known, calculation of a posterior moment or posterior quantile of interest from eqn [1] will define an additional integration problem that would likely lack a closed-form solution.
Fortunately, recent simulation-based methods like the Gibbs sampler and M–H algorithms offer convenient and powerful numerical strategies for the calculation of statistics and features of eqn [1]. These algorithms deliver a series of draws, say, θ(0),θ(1),θ(2),,,, that are constructed to converge in distribution to the joint posterior described in eqn [1]. The draws are Markovian, with the value of the draw at iteration t+1 depending on the current parameter value θ(t). Once convergence to the target density is ‘achieved’ these draws can be used in the same way as one would use direct Monte Carlo integration in order to calculate posterior means, posterior standard deviations, and other posterior statistics. For example, in order to estimate a posterior mean of θ, one can simply take a sample average of the simulated θ draws. In practice, care should be taken to diagnose that the parameter chain has converged to the target density, to discard an initial set of the preconvergence draws (often called a burn-in period), and then to use the postconvergence sample to calculate the desired quantities.
The postconvergence draws that is obtained using these iterative methods will prove to be correlated, as the distribution of, say, θ(t) depends on the last parameter sampled in the chain, θ(t-1).
If the correlation among the draws is severe, it may prove to be difficult to traverse the entire parameter space, and the numerical standard errors associated with the point estimates can be quite large.
With this general preview of the methods in place, and broad concerns regarding their performance in mind, the details of two commonly used simulation-based methods for Bayesian estimation and inference will now be discussed.
The Gibbs Sampler
Let θ be a K×1 parameter vector with associated posterior distribution p(θ|y) and write θ=[θ1 θ2…θK]. The Gibbs sampling algorithm proceeds as follows:
(i) Select an initial parameter vector θ(0)=[θ1(0)θ2(0)…θK(0)].
This initial value could be arbitrarily chosen, sampled from the prior, or perhaps could be obtained from a crude estimation method such as least squares.
(1) Sample θ1(1) from the complete posterior conditional density:
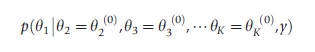
(2) Sample θ2(1) from p(θ2|θ1=θ1(1),θ3=θ3(0),…,θK=θK(0),y).
(K) Sample θ2(1) from p(θK|θ1=θ1(1),θ2=θ2(1),…,θK-1=θK-1(1),y)
(ii) Repeatedly cycle through (1)-(K) to obtain θ(2)= [θ1(2) θ2(2) θK(2)], θ(3), etc., always conditioning on the most recent values of the parameters drawn (e.g., to obtain θ1(2), draw from p(θ1|θ2=θ2(1)+,θK(1),…θK=θK(1),y), etc.). Also note that some groups of parameters can be blocked together (such as a full vector of regression parameters) and the conditionals in (1)–(K) need not be univariate.
To implement the Gibbs sampler, the ability to draw from the posterior conditionals of the model is required. Although the joint posterior density p(θ|) may often be intractable, the complete conditionals prove to be of standard forms in many cases, particularly in hierarchical models and latent variable models using data augmentation. For this reason, the Gibbs sampler is now routinely used to fit a variety of popular econometric models. An illustration of the power of the Gibbs algorithm will be provided in the following sections.
The Metropolis–Hastings algorithm
The M–H algorithm is an accept–reject type of algorithm in which a candidate value, say θc, is proposed, and then one decides whether to set θ(t+1) (the next value of the chain) equal to θc or to remain at the current value of the chain, θ(t). Formally, let P(θ|θ(t)) be an approximating proposal density (where the potential dependence on the current value of the chain is made explicit), and consider generating samples from P(θ|θ(t)) instead of the target distribution p(θ|y). Supposing that θc is sampled from P(·|θ(t)), set θ(t+1)=θc with (M–H) probability
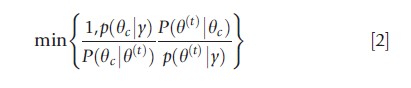
and otherwise set θ(t+1) =θ(t). In the case of a symmetric proposal density (the original Metropolis algorithm), the above probability of acceptance reduces to p(θc|y)/p(θ(t)|y), wherefrom candidate draws from regions of higher density are always accepted in the algorithm, and draws from regions of lower density are occasionally accepted.
The Gibbs sampler and the M–H algorithms are often used in combination in a given application. For example, it might be the case that the complete conditionals for K-1 of the elements of y have convenient functional forms, wherefrom the Gibbs sampler can be used to sample from these K-1 posterior conditionals. The complete conditional for the remaining parameter, however, may not take a standard form, and for this parameter, one could use the M–H algorithm to generate samples. This type of sampling is often (though mostly inappropriately) referred to as a ‘Metropolis-within-Gibbs’ step, and in (partially) nonconjugate situations, the use of both algorithms in combination often proves to be computationally attractive.
To illustrate the application of Markov Chain Monte Carlo (MCMC) methods in practice (and the Gibbs sampler in particular), the following section provides a simple example in the context of the LRM.
A Simple Linear Regression Example
To serve as a starting point, consider estimation and posterior prediction in an LRM. The goal in this section is to review a Gibbs sampling algorithm for the basic linear model, to briefly discuss methods for diagnosing convergence of a posterior simulator, and to illustrate how the posterior simulations can be used to calculate a variety of objects of interest. Under the assumption of conditionally normally distributed errors and homoskedasticity, the linear model can be written as:
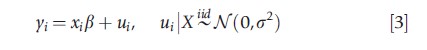
where xi is a 1×k vector of covariate data and N (μ, σ2) denotes a normal distribution with mean μ and variance σ2.
The likelihood function is implied by eqn [3], and a Bayesian analysis is completed by specifying prior distributions for the model parameters which, for this model, are β and σ2. Here, priors that are conditionally conjugate are specified, meaning that they combine naturally with the likelihood and will yield conditional posterior distributions that are of the same distributional families as the priors. Specifically,
![]()
![]()
are chosen, with IG(a, b) denoting an inverse gamma density with parameters a and b. The hyperparameters μβ,Vβ,a and b are chosen by the researcher to accord with their prior beliefs and, often, are specified so that the prior densities will be quite flat over a large region of the parameter space.
To effect a Gibbs sampling scheme for fitting this model, the conditional posterior distributions β|σ2, y and σ2|β, y are required. With a bit of algebra, one can show that these conditional distributions are normal and inverse gamma, respectively. The conditional posterior mean of β can be expressed as a matrix-weighted average of the prior mean μβ and the OLS estimate β=(X`X)-1X`y. As the size of the data set (n) grows, this posterior mean places increasing weight on the OLS estimate and, given a fixed prior, equals the OLS estimator in the limit. Similarly, the conditional posterior mean of σ2, E(σ2|β,y), can be written as a simple weighted average of the prior mean and the maximum likelihood estimate (given β), σ2=(y-Xβ)`(y-Xβ)/n. For fixed a and b it is again the case that as n→∞, the conditional posterior mean collapses on σ2.
A Gibbs algorithm for fitting this model, as previously discussed in the Section How It Works, involves iteratively sampling from the conditional multivariate normal density β|σ2, y and the inverse gamma density σ2|β, y. Although routines for sampling from a multivariate normal are well known, sampling from the inverse gamma is probably less familiar, although equally easy to do, as such a simulation can be obtained by inverting a draw from a gamma distribution.
Obesity Example
To fix ideas, a specific LRM using a sample of female data (n = 1782) from the study of Kline and Tobias (2008) is considered. These authors used data from the British Cohort study and sought to estimate the impact of BMI on labor market earnings. The regression of interest used in this study, therefore, uses log wages as the dependent variable and also includes an obesity indicator (BMI≥30), tenure on the current job (and its square), family income, a high school completion indicator, an indicator for an A-level degree, an indicator for a college degree, and finally, union and marriage indicators as controls.
To fit this model, the Gibbs sampler is run for 5500 iterations and the first 500 of these are discarded as a burn-in period. Recall from the previous Section The Gibbs sampler that Gibbs is an iterative algorithm – eventually the samples that are produced will represent a correlated set of draws from the posterior, although the initial set of simulations may not have converged to the posterior. To mitigate such effects, the first 500 draws are thrown out and the final 5000 simulations are used to calculate posterior means and standard deviations of parameters of interest. For the priors, fairly noninformative choices are made by setting μβ=0, Vβ=100Ik, a=3 and b=2.5.
Convergence Diagnostics And Mixing
Before discussing the estimation results, the issue of convergence of the MCMC sampler used in the study is first considered and it is sought to determine if 500 draws represent an adequate burn-in period for the application. One popular method for assessing convergence is to repeat the Gibbs analysis several times, each time using a different set of starting values, where the starting values are typically chosen to be intentionally ‘extreme’ so that the progression of the parameter draws can be clearly monitored as they move toward exploring the common posterior surface.
Figure 1 presents graphical results of such an exercise, which is denoted as a trace plot in the literature. Here, three separate Gibbs chains are run: one starting with β=0 (for all elements of the coefficient vector), a second starting with β=5, and a third starting with β=-5. The top portion of the figure plots the path of a representative coefficient – the coefficient on obesity, denoted bobesity, from all three Gibbs samplers (not plotting the initial condition itself). The lower panel similarly plots the paths of σ2 for all three chains. If the paths of these parameters from the three separate chains reveal no intersection, this provides evidence that the samplers have not yet converged, that a longer burn-in period is required, and potentially, that the algorithm itself may need to be refined in order to accelerate convergence. However, if it is observed that the simulations quickly move away from their overdispersed (and incorrect) starting values to eventually explore a common region of the parameter space, this provides evidence of convergence within the viewed number of iterations.
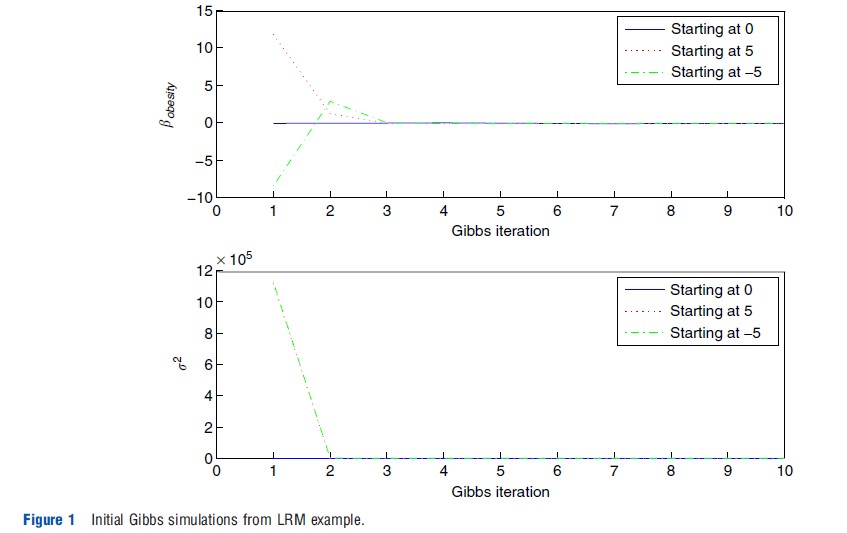
As Figure 1 clearly suggests, within just three iterations, the three separate chains appear to settle down and explore the same region of the parameter space. When starting with the unreasonable values of β=5 or β=-5, the first few iterations of the sampler produce very large values of the variance parameter σ2, which is not at all surprising given the extent to which the very early values of β are far from the mass of the posterior density. However, within just three iterations, it appears as if the variance parameter simulations shake off the influence of these starting values and then settle down to explore a common area.
The evidence offered by these graphs is that convergence to the posterior happens very quickly in the example: by discarding the first 500 iterations, one can credibly guard oneself against the problem that the early set of simulations produced by the chosen sampler are not draws from the joint posterior distribution and should not be used in the calculations.
Figure 2 offers a second trace plot, but this time graphs of the first 50 postconvergence simulations obtained from the sampler (i.e., the draws obtained from iterations 501–550 for each of the three chains). The obesity coefficient is provided in the top panel and the variance parameter in the bottom panel. First note the tremendous refinement in scale in Figure 2 relative to Figure 1: The data convey substantial information regarding these parameters, and once convergence has been achieved, the simulations explore the posterior surface and are no longer influenced by initial conditions. Second, the three separate chains appear to have very similar properties, such as means and variances, again providing evidence of convergence. Finally, the graphs also speak of the mixing of the chains. If the draws in a Gibbs algorithm are highly correlated, then the trace plot will reveal very long cycles. The plot in Figure 2, however, does not appear to exhibit any type of strong cyclical behavior and, instead, appears more like that of an electroencephalography, as can be seen under iid sampling from the posterior distribution.
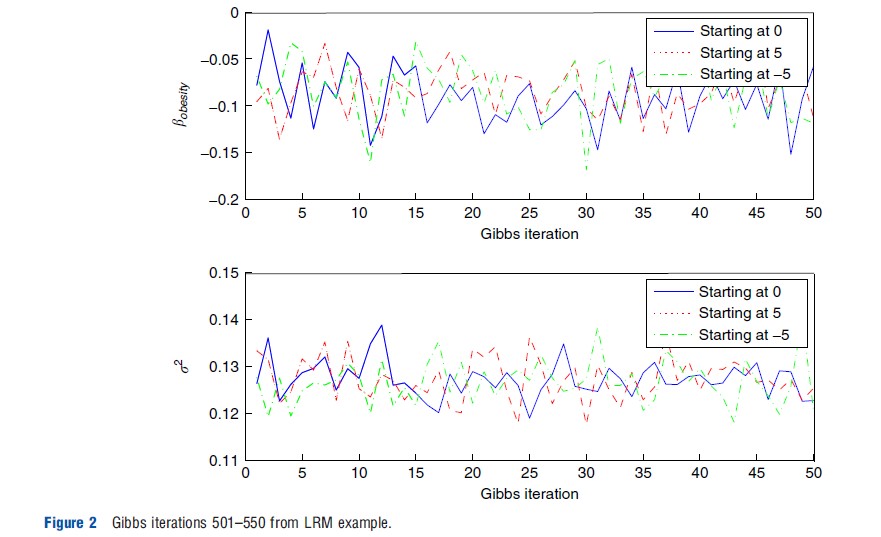
A more formal procedure one could use here in order to assess the mixing of the simulations is to report the so-called inefficiency factors for the parameters. These quantify the loss from adopting a Gibbs or M–H sampling approach (whose draws are autocorrelated) relative to an iid sampling scheme. These inefficiency factors can be obtained by calculating:

where pk(j) refers to the lag-j autocorrelation for parameter k. These can be calculated from the simulated output by simply computing the correlation between simulations j iterations apart. The upper limit of the summation, J, is typically chosen in accord with some type of rule of thumb – for example, once the lag-J correlation is smaller than, say, .05, the contribution of lag-t correlations, for all t>J.
When ineffk is near 1, the mixing of the posterior simulations is near the iid ideal. The value of ineffk is also directly interpretable: If a value equal to c>1 is obtained, this implies that one must run the sampler for c×M iterations in order to reproduce the numerical efficiency found in M iid simulations. For this linear regression example, it is found that the inefficiency factors for all parameters are very close to 1, indicating that the Gibbs algorithm effectively mimics the performance of iid sampling from the joint posterior.
Estimation Results
Presented in Table 1 are posterior means, posterior standard deviations, and posterior probabilities of being positive for the parameters of the LRM used in the study. For reference, the first column also reports OLS coefficient estimates, which are seen to be virtually indistinguishable from the reported posterior means, which is to be expected with (n=1782) and fairly noninformative priors. With respect to the key parameter of interest, it is found that obesity clearly has a negative impact on log wages, and this finding can be summarized via the statement: [ Pr (βobese<0|y)≈.999]. In terms of the point estimate, obese females earn approximately 8.2 % less, on average, than women who are not obese. With respect to the quantity Pr (βobese<0|y)≈.999, note that it offers a very natural interpretation of the evidence at hand: conditioned on the model, the priors, and the observed data, it can be confidently (nearly certain) claimed that obesity has a negative effect on wages.
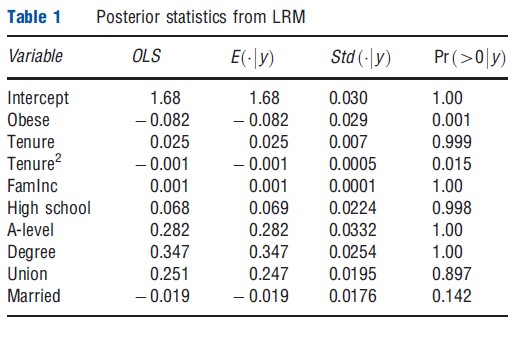
Although the Bayesian posterior probabilities reported in the final column of Table 1 may seem somewhat similar to the frequentist p-value, it is important to recognize that they are vastly different in terms of interpretation. First, such statements are entirely inappropriate in the classical paradigm, as βobese is a fixed parameter and is, therefore, either negative, positive, or zero. The probability statement that the Bayesian is able to provide, however, seems to be exactly what was expected to obtain from the analysis and offers a very useful quantity to offer to medical professionals and/or policy makers. Second, any probabilistic interpretation of effects in the frequentist case is derived from the sampling distribution of the estimator, highlighting the fact that such an approach places primary importance on what estimates one may have obtained had other data sets actually been observed. For the Bayesian, this sense of importance is misplaced, as decisions and recommendations should be based on the data at hand, and averaging over data sets that could have been observed, but were not, is neither advisable nor relevant.
Posterior Prediction
The last exercise focuses on posterior prediction. Here, it is sought to move beyond the narrow (and too often terminal) goal of parameter estimation to use the model to make predictions about future outcomes. In the context of the LRM used in this study, let wf denote the hourly wage (not log wage) of the individual, and let xf denote a given set of fixed characteristics. Because the predictive outcome wf=exp(yf) is a function of the regression parameters β and σ2, the posterior predictive distribution of wf via simulation is numerically approximated. That is, for every β(r) and σ2,(r) simulation from the posterior, it can be simply calculated as:

where ε(r)~iidN(0,1). Proceeding in this way generates a series of draws from the posterior predictive wage distribution – one draw obtained for each (β, σ2) simulation from the joint posterior.
In Figure 3 this approach is used and posterior predictive wage distributions are reported for obese and nonobese females, keeping the other explanatory variables constant and approximately equal to overall sample mean values. These densities are obtained by kernel-smoothing the simulated draws from the posterior predictive density.
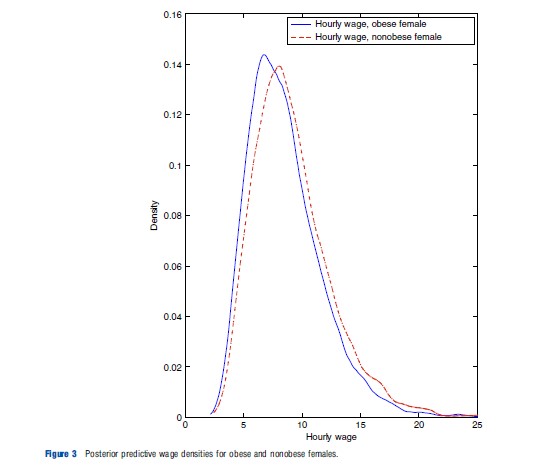
As shown in the figure, the wage density for the nonobese female is right-shifted relative to that of the obese female. To contrast this with a frequentist alternative, note that such an approach would likely proceed by plugging in point estimates of β and σ2 into an expression for the hourly wage density. Although such an expression can be analytically derived in this particular example (i.e., the wage density is lognormal), this exercise can often require a messy change of variables. Furthermore, such an approach suppresses parameter uncertainty and instead conditions on values of the parameter point estimates. The Bayesian approach to this exercise is quite appealing by comparison, as simulations can be used in place of analytic derivations, and parameter uncertainty is automatically accounted for, as they are properly integrated out to obtain the posterior predictive distribution p(wf|xf,y).
Bayesian Inference In Latent Variable Models
Although useful as a starting point and surely of interest in its own right, the previous treatment of the LRM is far from fully satisfactory, as it does not cover Bayesian model fitting in wide array of alternate models – including nonlinear and limited dependent variable models, for example – that are widely used in health research. In this section, a very general structure that nests many popular nonlinear microeconometric models is, therefore, introduced and posterior simulation for this general case is discussed. To this end, consider the following specification:

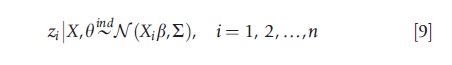
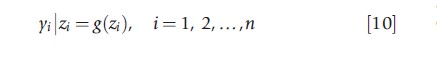
Equation [8] introduces a prior for the model parameters, consisting of a set of regression coefficients β and an inverse covariance matrix ∑-1. Equation [9] depicts the generation of a (potentially) multivariate latent variable zi, whereas eqn [10] links the observed outcomes yi to the latent data zi.
The generality of eqns [8]–[10] should not be overlooked. To illustrate, note for a univariate outcome yi:
- The probit model is a special case of eqns [8]–[10], where zi is a scalar, ∑-1 is absent from the model (i.e., the scalar variance parameter is normalized to unity), and eqn [10] specializes to yi=I(zi>0), where I(·) denotes the standard indicator function.
- The tobit model is produced when zi is a scalar, ∑=σ2 is a scalar variance parameter, and eqn [10] specializes to yi= max{0,zi}.
- The ordered probit model is produced when zi is a scalar, ∑-1 is absent from the model, and the observed data is connected to the latent data via a cutpoint vector: a:
![]()
In this final instance, eqn [10] must be generalized to allow the link between latent and observed outcomes to depend on the cutpoint vector a.
The equations outlined in eqns [8]–[10] also cover a wide variety of multivariate models. For example, the seemingly unrelated regressions model, the hurdle and sample selection models, generalized tobit models, multivariate ordinal models, models with continuous and discrete endogenous variables (as discussed in more detail below), and the multivariate probit (MVP) and multinomial probit (MNP) models can be regarded as specific cases of this general structure. As such, knowing how to estimate a system of equations like eqns [8]–[10] enables the applied researcher to estimate a wide variety of popular microeconometric models.
Applying the idea of data augmentation, the latent data z in eqn [9] can be treated like another parameter of the model, giving rise to the augmented joint posterior distribution p(z,β,∑-1|y). A Gibbs sampler, then, draws from each of the three constituent posterior conditional distributions.
In some models, the required simulations are almost trivially performed, whereas other specifications will demand refinement of any general scheme. In many cases, β will be sampled from a multivariate normal, ∑-1 from a Wishart distribution, and zi from a truncated normal. Posterior simulation in the probit model, for example, simply involves generation of a multivariate normal random variable for sampling b and a series of (independent) univariate truncated normals for sampling the latent data z. In terms of the latter, the observed binary response yi serves to truncate the value of the latent variable: yi=1 indicates that zi must be positive, whereas yi = 0 restricts zi to be nonpositive. In the MNP and MVP models, however, additional care must be taken to normalize the associated variance parameter(s) to unity. The general sampling of the latent data will also prove more challenging in some models than in others, and an appropriate method of sampling the latent data must be carefully considered for the model in question.
With these practical implementation details noted, the reader should still recognize the generality and scope of coverage that the simple description of eqns [8]–[10] offers, as well as the fact that in many cases, nonlinear model fitting only requires the ability to sample from standard distributions (such as the normal, truncated normal, and Wishart). Further details and associated References: regarding a variety of specific models are provided in the further reading section of this article.
Posterior Simulation With An Endogenous Binary Variable
To provide a specific example of a popular model ‘covered’ by eqns [8]–[10], the well-studied case of a continuous outcome model with a dummy endogenous variable is considered. In this case, eqn [9] might specialize to:

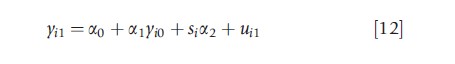
where
![]()
Equation [11] is a latent variable equation governing the generation of an endogenous binary outcome yi0. The variable y1 is a continuous outcome variable, which is completely observed. The variables r and s are assumed to be exogenous, with r containing at least one element that is not in s.
With a bit of finesse, this bivariate system of equations can also be mapped into the form of the system in eqn [9]. In terms of posterior simulation, the variables can be stacked and the vector of parameters β=[y a0 a1 a2] can be sampled from a multivariate normal. A straightforward reparameterization of the problem enables the simulation of the variance parameter σ21 and the covariance between the errors of eqns [11] and [12], denoted σ01. Finally, the latent data zi0 can be sampled from a univariate truncated normal, where the region of truncation is governed by the observed value yi0.
Obesity Example, Revisited
For illustration purposes and to expand the application of Section 3 (where the potential endogeneity of female obesity was ignored), the binary endogenous variable model of Section 1 is fitted and applied to wage/obesity data. The continuous outcome yi1 remains the log hourly wage and the binary endogenous variable yi0 is the obesity indicator. The covariates in the wage equation remain the same as those employed in Section 2, whereas in eqn [11] maternal and paternal BMI are included as exclusion restrictions (i.e., variables that are assumed to affect the respondent’s BMI but have no conditional effect on the respondent’s log wage). In addition, this equation also includes a set of education indicators, family income and a marriage indicator. The Gibbs algorithm is run for 10 000 iterations, with the first 1000 discarded as the burn-in. Results of this analysis are provided in Table 2.
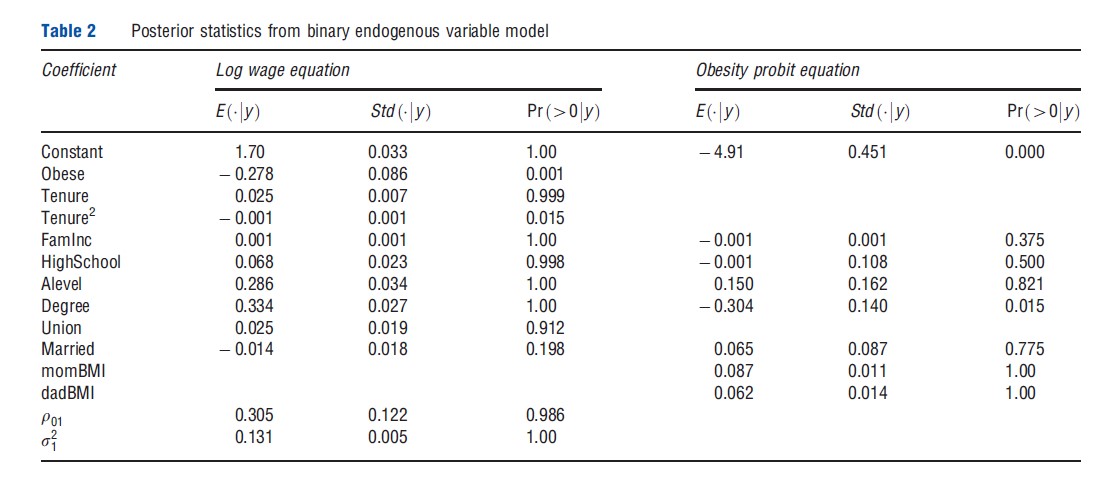
Apart from the values of the obesity and union coefficients, the values of the log wage regression coefficients remain very similar to those presented in Table 1. In the obesity equation, consistent with the prior expectations, strong evidence that higher parental BMI leads to a higher likelihood of child obesity and that the college educated have lower rates of obesityis found.
The interesting difference in results relative to those in Table 1 lies in the estimated impact of obesity on log wages and its interpretation. As shown in the second-to-last row of Table 2, p01 is found to be positive with very high posterior probability. One interpretation of this result, which is also offered by Kline and Tobias, 2008, is that individuals who are very dedicated to their job, perhaps working long hours in order to earn a high conditional wage, may forego investments in health capital in order to earn such a wage. As a result, unobserved factors leading an individual to earn a high conditional wage will also positively correlate with unobservables affecting the production of obesity, consistent with the positive value of r01 in Table 2. The results in Table 1, then, have presented a conservative estimate of the obesity penalty, as they have combined the actual obesity penalty with an effect arising from unobservable characteristics of productive workers that also contribute to obesity. When separating these effects, as the analysis of Table 2 seeks to do, a much larger estimate of the obesity penalty is seen, as the coefficient has increased (in an absolute sense) more than three-fold, with a posterior mean now equal to -.278.
Although the specific results of this application are of secondary importance, what is most important to appreciate is the relative ease with which these results have been obtained; fitting the model only required the ability to draw from normal, inverse gamma and univariate truncated normal distributions. This simplicity is not specific to the model considered here but applies to many specifications that fall within the class of models described by eqns [8]–[10]. Given the relative ease with which parameter and latent variable simulations can be obtained from the joint posterior, it then becomes easy to move beyond point estimation to calculate marginal effects and to conduct various counterfactual or policy experiments.
Conclusion
This article has reviewed the basics of the Bayesian approach to estimation and inference, focusing in particular on applications of the Gibbs sampler and M–H algorithms. In conjunction with data augmentation, these algorithms greatly ease estimation in a variety of microeconometric models, many of which are commonly employed in health economics applications. Although the material presented here only offers a superficial review of the Bayesian approach, the References: provided contain significantly more information on both the theory and application of these methods.
References:
- Kline, B. and Tobias, J. L. (2008). The wages of BMI: Bayesian analysis of a skewed treatment-response model with nonparametric endogeneity. Journal of Applied Econometrics 23, 767–793.
- Albert, J. H. and Chib, S. (1993). Bayesian analysis of binary and polychotomous response data. Journal of the American Statistical Association 88, 669–679.
- Chib, S. (2012). MCMC methods. In Geweke, J., Koop, G. and van Dijk, H. (eds.) Handbook of Bayesian econometrics, pp 183–220. Oxford: Oxford University Press.
- Gelfand, A., Hills, S., Racine-Poon, A. and Smith, A. (1990). Illustration of Bayesian inference in normal data models using gibbs sampling. Journal of the American Statistical Association 85, 972–985.
- Geweke, J. (2005). Contemporary Bayesian econometrics and statistics. Hoboken, NJ: John Wiley & Sons.
- Geweke, J. and Keane, M. (2001). Computationally intensive methods for integration in econometrics. In Heckman, J. J. and Leamer, E. (eds.) Handbook of Econometrics, vol. 5, pp 3463–3568. Amsterdam, The Netherlands: Elsevier.
- Greenberg, E. (2008). Introduction to Bayesian econometrics. New York: Cambridge University Press.
- Koop, G. (2003). Bayesian econometrics. Hoboken, NJ: John Wiley & Sons.
- Koop, G., Poirier, D. J. and Tobias, J. L. (2007). Bayesian econometric methods. New York: Cambridge University Press.
- Lancaster, A. (2004). An introduction to modern Bayesian econometrics. Malden, MA: Blackwell Publishing.
- Lopes, H. and Tobias, J. L. (2011). Confronting prior convictions: On issues of prior sensitivity and likelihood robustness in Bayesian analysis. Annual Review of Economics 3, 107–131.
- Poirier, D. J. (1995). Intermediate statistics and econometrics: A comparative approach. Cambridge, MA: MIT Press.
- Rossi, P. E., Allenby, G. M. and McCulloch, R. (2005). Bayesian statistics and marketing. Hoboken, NJ: John Wiley & Sons.
- Train, K. E. (2009). Discrete choice methods with simulation. New York: Cambridge University Press.
- Zellner, A. (1971). An introduction to Bayesian inference in econometrics. Malabar, FL: Krieger Publishing Company.