Introduction
Today an understanding of health is not complete without considering the role of in utero and intergenerational effects. The recent popularity of the fetal origins hypothesis, asserting that early life influences through the fetal environment (e.g., nutritional deprivation) have latent long-run effects on health, has nudged economists to think about the production of health beginning much earlier in life. This hypothesis, complemented with economic theories of parental investment characterizes how important early-life factors can be in explaining adult health.
The goal of this article is to give the reader a framework and an understanding of the strength of in utero and intergenerational influences. To provide a concrete structure to interpret these effects, the authors first outline a multiperiod investment model akin to the work of James Heckman that translates early life circumstances to health in adulthood. With such a mathematical model, one can be very specific about the roles of the in utero and intergenerational environments. Before discussing the various inputs into the health production function, the authors consider possible measures of health in utero and at birth. The bulk of the article then discusses how various inputs (e.g., maternal nutrition, sickness, maternal age, maternal education, family income, employment, maternal health behaviors, and environmental exposure) impact health using the Heckman investment model as a guide.
Theoretical Framework
Economic Framework For The Link Between In Utero And Early Life Conditions And Later Health
Under traditional economic models of health, there is little room for early life and in utero events to impact later health. More recently developed models, however, demonstrate the importance of investment and events in early life for health production. Models such as Heckman (2007) provide the mathematical structure to understand how early parental investment and initial endowments (e.g., health at birth) may affect adult health. These models invoke two important features: self-productivity and dynamic complementarity. Self-productivity embodies the notion that skills acquired in one period persist into other periods, and that higher levels of skills in one period can increase the amount of skills acquired in a later period. Dynamic complementarities embrace the idea that capabilities acquired in one period augment the productivity of investment in the future.
Consider a simplified model with two periods of childhood investment and a constant elasticity of substitution production function as Heckman (2007) does:
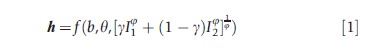
where h is a vector of adult capabilities in period 3 (adulthood), b are parental capabilities, θ is the initial endowment, It is investment in period t, 1/1-φ is the elasticity of substitution of inputs across periods, and g represents the net effect of I1 on h (the ‘capability multiplier’). One can think of h as including health and other capabilities such as education in adulthood. Investments can include nutrition and medical care in childhood. Parental characteristics such as income and education influence the choice of inputs (i.e., I1 and I2), either by shifting tastes, acting as a constraint on the ability to purchase inputs, or changing θ.
Self-productivity implies that δh/δIt>0 for t = 1,2; that is, in-vestment made in prior periods raises adult capabilities. Vaccinations would be one such example; the polio vaccine taken as a child nearly assures that as adult, an individual will not impeded by polio. Under dynamic complementarities, the function δ2h/δθδIt>0, meaning that the effect of investment is an increasing function of capabilities. As an example of dynamic complementarities, consider an early childhood investment made in period 1 (e.g., Head Start). This investment may augment childhood capabilities in period 2, which then will make formal schooling following Head Start more productive.
Under some simplifying assumptions, this general model can generate some useful insights about the possible role of early and in utero investments. First, the larger the capability multiplier (i.e., g) the higher the optimal ratio of early to late investment. Second, if early and late investments are perfect substitutes, disadvantage in period 1 can always be overcome with later investment. As the degree of substitution approaches N, optimal investment in period 1 is equal to optimal investment in period 2. Third, there is a tradeoff between investing in period 1 and investing in period 2. Owing to discounting, investment in period 2 is cheaper than investment of the same amount in period 1. This consideration pushes investment to period 2, but the productivity of investment in period 1 (i.e., the size of g) encourages investment in period 1.
This model can explain why early life investments, even if they are small in magnitude, can have effects on more longrun outcomes. Moreover, although this article discusses the importance of early and in utero conditions collectively, it may be important to distinguish between these even further. Specifically, in utero investments, because of the extended period allowed for dynamic complementarities, may be more important than early childhood investments.