Public Health Statistics

Nearly every day statistics are used to support assertions about health and what people can do to improve their health. The press frequently quotes scientific articles assessing the roles of diet, exercise, the environment, and access to medical care in maintaining and improving health. Because the effects are often small, and vary greatly from person to person, an understanding of statistics and how it allows researchers to draw conclusions from data is essential for every person interested in public health. Statistics is also of paramount importance in determining which claims regarding factors affecting our health are not valid, not supported by the data, or are based on faulty experimental design and observation.

When an assertion is made such as “electromagnetic fields are dangerous,” or “smoking causes lung cancer,” statistics plays a central role in determining the validity of such statements. Methods developed by statisticians are used to plan population surveys and to optimally design experiments aimed at collecting data that allows valid conclusions to be drawn, and thus either confirm or refute the assertions. Biostatisticians also develop the analytical tools necessary to derive the most appropriate conclusions based on the collected data.

Role Of Biostatistics In Public Health

In the Institute of Medicine’s report The Future of Public Health, the mission of public health is defined as assuring conditions in which people can be healthy. To achieve this mission three functions must be undertaken: (1) assessment, to identify problems related to the health of populations and determine their extent; (2) policy development, to prioritize the identified problems, determine possible interventions and/or preventive measures, set regulations in an effort to achieve change, and predict the effect of those changes on the population; and (3) assurance, to make certain that necessary services are provided to reach the desired goal—as determined by policy measures—and to monitor how well the regulators and other sectors of the society are complying with policy.

An additional theme that cuts across all of the above functions is evaluation, that is, how well are the functions described above being performed.

Biostatistics plays a key role in each of these functions. In assessment, the value of biostatistics lies in deciding what information to gather to identify health problems, in finding patterns in collected data, and in summarizing and presenting these in an effort to best describe the target population. In so doing, it may be necessary to design general surveys of the population and its needs, to plan experiments to supplement these surveys, and to assist scientists in estimating the extent of health problems and associated risk factors. Biostatisticians are adept at developing the necessary mathematical tools to measure the problems, to ascertain associations of risk factors with disease, and creating models to predict the effects of policy changes. They create the mathematical tools necessary to prioritize problems and to estimate costs, including undesirable side effects of preventive and curative measures.

In assurance and policy development, biostatisticians use sampling and estimation methods to study the factors related to compliance and outcome. Questions that can be addressed include whether an improvement is due to compliance or to something else, how best to measure compliance, and how to increase the compliance level in the target population. In analyzing survey data, biostatisticians take into account possible inaccuracies in responses and measurements, both intentional and unintentional. This effort includes how to design survey instruments in a way that checks for inaccuracies, and the development of techniques that correct for nonresponse or for missing observations. Finally, biostatisticians are directly involved in the evaluation of the effects of interventions and whether to attribute beneficial changes to policy.

Understanding Variation In Data

Nearly all observations in the health field show considerable variation from person to person, making it difficult to identify the effects of a given factor or intervention on a person’s health. Most people have heard of someone who smoked every day of his or her life and lived to be ninety, or of the death at age thirty of someone who never smoked. The key to sorting out seeming contradictions such as these is to study properly chosen groups of people (samples), and to look for the aggregate effect of something on one group as compared to another. Identifying a relationship, for example, between lung cancer and smoking, does not mean that everyone who smokes will get lung cancer, nor that if one refrains from smoking one will not die from lung cancer. It does mean, however, that the group of people who smoke are more likely than those who do not smoke to die from lung cancer.

How can we make statements about groups of people, but be unable to claim with any certainty that these statements apply to any given individual in the group? Statisticians do this through the use of models for the measurements, based on ideas of probability. For example, it can be said that the probability that an adult American male will die from lung cancer during one year is 9 in 100,000 for a nonsmoker, but is 190 in 100,000 for a smoker. Dying from lung cancer during a year is called an “event,” and “probability” is the science that describes the occurrence of such events. For a large group of people, quite accurate statements can be made about the occurrence of events, even though for specific individuals the occurrence is uncertain and unpredictable. A simple but useful model for the occurrence of an event can be made based on two important assumptions: (1) for a group of individuals, the probability that an event occurs is the same for all members of the group; and (2) whether or not a given person experiences the event does not affect whether others do. These assumptions are known as (1) common distribution for events, and (2) independence of events. This simple model can apply to all sorts of public health issues. Its wide applicability lies in the freedom it affords researchers in defining events and population groups to suit the situation being studied.

Consider the example of brain injury and helmet use among bicycle riders. Here groups can be defined by helmet use (yes/no), and the “event” is severe head injury resulting from a bicycle accident. Of course, more comprehensive models can be used, but the simple ones described here are the basis for much public health research. Table 1 presents hypothetical data about bicycle accidents and helmet use in thirty cases.

Table 1

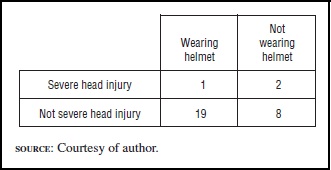
It can be seen that 20 percent (2 out of 10) of those not wearing a helmet sustained severe head injury, compared to only 5 percent (1 out of 20) among those wearing a helmet, for a relative risk of four to one. Is this convincing evidence? An application of probability tells us that it is not, and the reason is that with such a small number of cases, this difference in rates is just not that unusual. To better understand this concept, the meaning of probability and what conclusions can drawn after setting up a model for the data must be described.

Probability is the branch of mathematics that uses models to describe uncertainty in the occurrence of events. Suppose that the chance of severe head injury following a bicycle accident is one in ten. This risk can be simulated using a spinning disk with the numbers “1” through “10” equally spaced around its edge, with a pointer in the center to be spun. Since a spinner has no memory, spins will be independent. A spin will indicate severe head injury if a “1” shows up, and no severe head injury for “2” through “10.” The pointer could be spun ten times to see what could happen among ten people not wearing a helmet. The theory of probability uses the binomial distribution to tell you exactly what could happen with ten spins, and how likely each outcome is. For example, the probability that we would not see a “1” in ten spins is .349, the probability that we will see exactly one “1” in ten spins is .387, exactly two is .194, exactly three is .057, exactly four is .011, exactly five is .001, with negligible probability for six or more. So if this is a good model for head injury, the probability of two or more people experiencing severe head injury in ten accidents is .264.

A common procedure in statistical analysis is to hypothesize that no difference exists between two groups (called the “null” hypothesis) and then to use the theory of probability to determine how tenable such an hypothesis is. In the bicycle accident example, the null hypothesis states that the risk of injury is the same for both groups. Probability calculations then tell how likely it is under null hypothesis to observe a risk ratio of four or more in samples of twenty people wearing helmets and ten people not wearing helmets. With a common risk of injury equal to one in ten for both groups, and with these sample sizes, the surprising answer is that one will observe a risk ratio greater than four quite often, about 16 percent of the time, which is far too large to give us confidence in asserting that wearing helmets prevents head injury.

This is the essence of statistical hypothesis testing. One assumes that there is no difference in the occurrences of events in our comparison groups, and then calculates the probabilities of various outcomes. If one then observes something that has a low probability of happening given the assumption of no differences between groups, then one rejects the hypothesis and concludes that there is a difference. To thoroughly test whether helmet use does reduce the risk of head injury, it is necessary to observe a larger sample—large enough so that any observed differences between groups cannot be simply attributed to chance.

Sources Of Data

Data used for public health studies come from observational studies (as in the helmet, use example above), from planned experiments, and from carefully designed surveys of population groups. An example of a planned experiment is the use of a clinical trial to evaluate a new treatment for cancer. In these experiments, patients are randomly assigned to one of two groups—treatment or placebo (a mock treatment)—and then followed to ascertain whether the treatment affects clinical outcome. An example of a survey is the National Health and Nutrition Examination Survey (NHANES) conducted by the National Center for Health Statistics. NHANES consists of interviews of a carefully chosen subset of the population to determine their health status, but chosen so that the conclusions apply to the entire U.S. population.

Both planned experiments and surveys of populations can give very good data and conclusions, partly because the assumptions necessary for the underlying probability calculations are more likely to be true than for observational studies. Nonetheless, much of our knowledge about public health issues comes from observational studies, and as long as care is taken in the choice of subjects and in the analysis of the data, the conclusions can be valid.

The biggest problem arising from observational studies is inferring a cause-and-effect relationship between the variables studied. The original studies relating lung cancer to smoking showed a striking difference in smoking rates between lung cancer patients and other patients in the hospitals studied, but they did not prove that smoking was the cause of lung cancer. Indeed, some of the original arguments put forth by the tobacco companies followed this logic, stating that a significant association between factors does not by itself prove a causal relationship. Although statistical inference can point out interesting associations that could have a significant influence on public health policy and decision making, these statistical conclusions require further study to substantiate a cause-and-effect relationship, as has been done convincingly in the case of smoking.

A tremendous amount of recent data is readily available through the Internet. These include already tabulated observations and reports, as well as access to the raw data. Some of this data cannot be accessed through the Internet because of confidentiality requirements, but even in this case it is sometimes possible to get permission to analyze the data at a secure site under the supervision of employees of the agency. Described here are some of the key places to go for data on health. Full Internet addresses for the sites below can be found in the bibliography.

A comprehensive source can be found at Fedstats, which provides a gateway to over one hundred federal government agencies that compile publicly available data. The links here are rather comprehensive and include many not directly related to health. The key government agency providing statistics and data on the extent of the health, illness, and disability of the U.S. population is the National Center for Health Statistics (NCHS), which is one of the centers of the Centers for Disease Control and Prevention (CDC). The CDC provides data on morbidity, infectious and chronic diseases, occupational diseases and injuries, vaccine efficacy, and safety studies. All the centers of the CDC maintain online lists of their thousands of publications related to health, many of which are now available in electronic form. Other major governmental sources for health data are the National Cancer Institute (which is part of the National Institutes of Health), the U.S. Bureau of the Census, and the Bureau of Labor Statistics. The Agency for Healthcare Research and Quality is an excellent source for data relating to the quality, access, and medical effectiveness of health care in the United States. The National Highway and Traffic Safety Administration, in addition to publishing research reports on highway safety, provides data on traffic fatalities in the Fatality Analysis Reporting System, which can be queried to provide data on traffic fatalities in the United States.

A number of nongovernmental agencies share data or provide links to online data related to health. The American Public Health Association provides links to dozens of databases and research summaries. The American Cancer Society provides many links to data sources related to cancer. The Research Forum on Children, Families, and the New Federalism lists links to numerous studies and data on children’s health, including the National Survey of America’s Families.

Much of public health is concerned with international health, and the World Health Organization (WHO) makes available a large volume of data on international health issues, as well as provides links to its publications. The Center for International Earth Science Information Network provides data on world population, and its goals are to support scientists engaged in international research. The Internet provides an opportunity for health research unequaled in the history of public health. The accessibility, quality, and quantity of data are increasing so rapidly that anyone with an understanding of statistical methodology will soon be able to access the data necessary to answer questions relating to health.

Analysis Of Tabulated Data

One of the most commonly used statistical techniques in public health is the analysis of tabled data, which is generally referred to as “contingency table analysis.” In these tables, observed proportions of adverse events are compared in the columns of the table by a method known as a “chisquare test.” Such data can naturally arise from any of the three data collection schemes mentioned. In our helmet, for example, observational data from bicycle accidents were used to create a table with helmet use defining the columns, and head injury, the rows. In a clinical trial, the columns are defined by the treatment/placebo groups, and the rows by outcome (e.g., disease remission or not). In a population survey, columns can be different populations surveyed, and rows indicators of health status (e.g., availability of health insurance). The chi-square test assumes that there is no difference between groups, and calculates a statistic based on what would be expected if no difference truly existed, and on what is actually observed. The calculation of the test statistic and the conclusions proceed as follows:

1. The expected frequency (E) is calculated (assuming no difference) for each cell in the table by first adding to get the totals for each row, the totals for each column, and the grand total (equal to the total sample size); then for each cell we find the expected count: E = (rowtotal) (columntotal)/(grandtotal).
2. For each cell in the table, let O be the observed count, and calculate: (O-E)2/E.
3. The values from step 2 are summed over all cells in the table. This is the test statistic, X.
4. If X exceeds 3.96 for a table with four cells, then the contingency table is said to be statistically “significant.” If the sample and the resulting analysis is repeated a large number of times, this significant result will happen only 5 percent of the time when there truly is no difference between groups, and hence this is called a “5 percent significance test.”
5. For tables with more than two rows and/or columns different comparisons values are needed. For a table with six cells, we check to see if X is larger than 5.99, with eight cells, we compare X to 7.81, and for nine or ten cells we compare X to 9.49.
6. This method has problems if there are too many rows and columns and not enough observations. In such cases, the table should be reconfigured to have a smaller number of cells. If any of the E values in a table fall below five, some of the rows and/or columns should be combined to make all values of E five or more.

Suppose a larger data set is used for our helmet use/head injury example (see Table 2).

Table 2

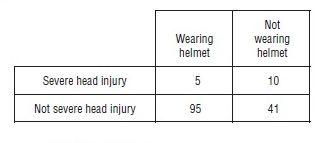
It is worthwhile noting that the proportions showing head injury for these data are almost the same as before, but that the sample size is now considerably larger, 151. Following the steps outlined above, the chi-square statistic can be calculated and conclusions can be drawn:

1. The total for the first column is 100, for the second column 51, for the first row 15, and for the second row 136. The grand total is 151, the total sample size. The expected frequencies, that is the “Es,” assuming no difference in injury rates between the helmet group and the no helmet group, are given in Table 3. It is quite possible for the Es to be non-integer, and if so, we keep the decimal part in all our calculations.
2. The values for (O-E)2/E are presented in Table 4.
3. X=8.055
4. Because this exceeds 3.84, we have a significant association between the helmet use and head injury, at the 5 percent level.

The chi-square procedure presented here is one of the most important analytic techniques used in public health research. Its simplicity allows it to be widely used and understood by nearly all professionals in the field, as well as by interested third parties. Much of what we know about what makes us healthy or what endangers our lives has been shown through the use of contingency tables.

Studying Relationships Among Variables

A major contribution to our knowledge of public health comes from understanding trends in disease rates and examining relationships among different predictors of health. Biostatisticians accomplish these analyses through the fitting of mathematical models to data. The models can vary from a simple straight-line fit to a scatter plot of XY observations, all the way to models with a variety of nonlinear multiple predictors whose effects change over time. Before beginning the task of model fitting, the biostatistician must first be thoroughly familiar with the science behind the measurements, be this biology, medicine, economics, or psychology. This is because the process must begin with an appropriate choice of a model. Major tools used in this process include graphics programs for personal computers, which allow the biostatistician to visually examine complex relationships among multiple measurements on subjects.

The simplest graph is a two-variable scatter plot, using the y-axis to represent a response variable of interest (the outcome measurement), and the x-axis for the predictor, or explanatory, variable. Typically, both the x and y measurements take on a whole range of values—commonly referred to as continuous measurements, or sometimes as quantitative variables. Consider, for example, the serious health problem of high bloodlead levels in children, known to cause serious brain and neurologic damage at levels as low as 10 micrograms per deciliter. Since lead was removed from gasoline, blood-levels of lead in children in the United States have been steadily declining, but there is still a residual risk from environmental pollution. One way to assess this problem is to relate soil-lead levels to blood levels in a survey of children—taking a measurement of the blood-lead concentration on each child, and measuring the soil-lead concentration (in milligrams per kilogram) from a sample of soil near their residences. As is often the case, a plot of the blood levels and soil concentrations shows some curvature, so transformations of the measurements are taken to make the relationship more nearly linear. Choices commonly used for transforming data include taking square roots, logarithms, and sometimes reciprocals of the measurements. For the case of lead, logarithms of both the blood levels and of the soil concentrations produce an approximately linear relationship. Of course, this is not a perfect relationship, so, when plotted, the data will appear as a cloud of points as shown in Figure 1.

Figure 1

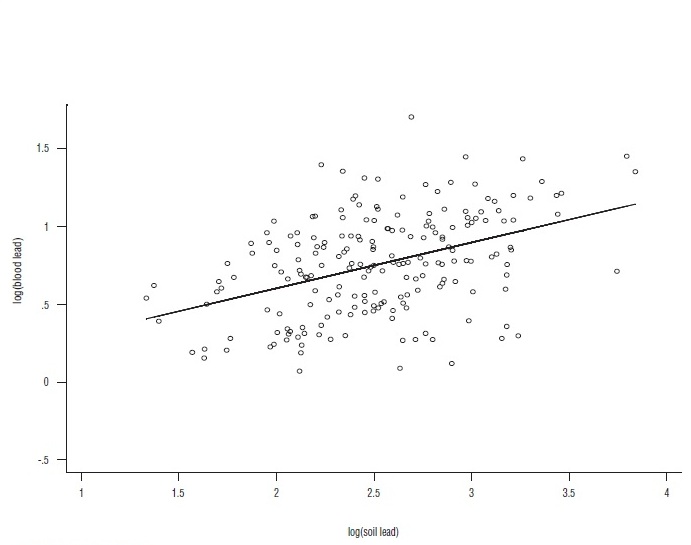
This plot, representing two hundred children, was produced by a statistical software program called Stata, using, as input, values from a number of different studies on this subject. On the graph, the software program plotted the fitted straight line to the data, called the regression equation of y on x. The software also prints out the fitted regression equation: y = .29x + .01. How does one interpret this regression? First, it is not appropriate to interpret it for an individual; it applies to the population from which the sample was taken. It says that a increase of 1 in log (soil-lead) concentration will correspond, on average, to an increase in log (blood-lead) of .29. To predict the average blood-lead level given a value for soil lead, the entire equation is used. For example, a soil-lead level of 1,000 milligrams per kilogram, whose log is three, predicts an average log blood-lead level of .29×3 + .01 = .57, corresponding to a measured blood level of 7.6 micrograms per deciliter. The main point is that, from the public health viewpoint, there is a positive relationship between the level of lead in the soil and blood-lead levels in the population. An alternative interpretation is to state that soil-lead and blood-lead levels are positively correlated.

As in the case of contingency tables, the significance of the regression can be tested. In this case, as in all of statistics, statistical significance does not refer to the scientific importance of the relationship, but rather to a test of whether or not the observed relationship is the result of random association. Every statistical software package for personal computers includes a test of significance as part of its standard output. These packages, and some hand calculators, along with the line itself, will produce an estimate of the correlation between the two variables, called the correlation coefficient, or “r.” If t is larger than 2, or smaller than -2, the regression is declared significant at the 5 percent level. For the data in Figure 1, r is 0.42. This number can very easily be used to test for the statistical significance of the regression through the following formula:

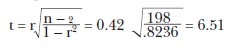
The number “r” calculated this way must lie between -l and +1, and is often interpreted as a measure of how close to a straight line the data lie. Values near ±1 indicate a nearly perfect linear relationship, while values near 0 indicate no linear relationship. It is important not to make the mistake of interpreting r near 0 as meaning there is no relationship whatever—a curved relation can lead to low values of r.

The relationship between soil-lead and bloodlead could be studied using the contingency table analysis discussed earlier. For each child, both the soil-lead levels and the blood-lead levels could be classified as high or low, choosing appropriate criteria for the definitions of high and low. This too would have shown a relationship, but it would not be as powerful, nor would it have quantified the relationship between the two measurements as the regression did. Choosing a cutoff value for low and high on each measurement that divides each group into two equal-size subgroups as shown in Table 5.

Table 5

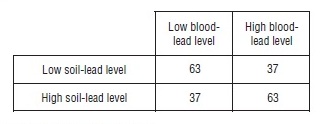
The chi-square statistic calculated from this table is 13.5, which also indicates an association between blood-lead level and soil-lead levels in children. The conclusion is not as compelling as in the linear regression analysis, and a lot of information in the data has been lost by simplifying them in this way. One benefit, however, of this simpler analysis is that we do not have to take logarithms of the data and worry about the appropriate choice of a model.

Regression is a very powerful tool, and it is used for many different data analyses. It can be used to compare quantitative measurements on two groups by setting x = 1 for each subject in group one, and setting x = 2 for each subject in group two. The resulting analysis is equivalent to the two-sample t-test discussed in every elementary statistics text.

The most common application of regression analysis occurs when an investigator wishes to relate an outcome measurement y to several x variables—multiple linear regression. For example, regression can be used to relate blood lead to soil lead, environmental dust, income, education, and sex. Note that, as in this example, the x variables can be either quantitative, such as soil lead, or qualitative, such as sex, and they can be used together in the same equation. The statistical software will easily fit the regression equation and print out significance tests for each explanatory variable and for the model as a whole. When we have more than one x variable, there is no simple way to perform the calculations (or to represent them) and one must rely on a statistical package to do the work.

Regression methods are easily extended to compare a continuous response measurement across several groups—this is known as analysis of variance, also discussed in every elementary statistics text. It is done by choosing for the x variables indicators for the different groups—so-called dummy variables.

An important special case of multiple linear regression occurs when the outcome measurement y is dichotomous—indicating presence or absence of an attribute. In fact, this technique, called logistic regression, is one of the most commonly used statistical techniques in public health research today, and every statistical software package includes one or more programs to perform the analysis. The predictor x-variables used for logistic regression are almost always a mixture of quantitative and qualitative variables. When only qualitative variables are used, the result is essentially equivalent to a complicated contingency table analysis.

Methods of regression and correlation are essential tools for biostatisticians and public health researchers when studying complex relationships among different quantitative and qualitative measurements related to health. Many of the studies widely quoted in the public health literature have relied on this powerful technique to reach their conclusions.

Bibliography:

1. Afifi, A. A., and Clark, V. A. (1996). Computer-Aided Multivariate Analysis, 3rd edition. London: Chapman and Hall.
2. Armitage, P., and Berry, G. (1994). Statistical Methods in Medical Research. Oxford: Blackwell Science.
3. Doll, R., and Hill, A. B. (1950). “Smoking and Carcinoma of the Lung. Preliminary Report.” British Medical Journal 13:739–748.
4. Dunn, O. J., and Clark, V. A. (2001). Basic Statistics, 3rd edition. New York: John Wiley and Sons.
5. Glantz, S. A., and Slinker, B. K. (2001). Primer of Applied Regression and Analysis of Variance. New York: McGraw- Hill.
6. Hosmer, D. W., and Lemeshow, S. (2000). Applied Logistic Regression. New York: John Wiley and Sons.
7. Institute of Medicine. Committee for the Study of the Future of Public Health (1988). The Future of Public Health. Washington, DC: National Academy Press.
8. Kheifets, L.; Afifa, A. A.; Buffler, P. A.; and Zhang, Z. W. (1995). “Occupational Electric and Magnetic Field Exposure and Brain Cancer: A Meta-Analysis.” Journal of Occupational and Environmental Medicine 37:1327–1341.
9. Lewin, M. D.; Sarasua, S.; and Jones, P. A. (1999). “A Multivariate Linear Regression Model for Predicting Children’s Blood Lead Levels Based on Soil Lead Levels: A Study at Four Superfund Sites.” Environmental Research 81(A):52–61.
10. National Center for Health Statistics (1996). NHANES: National Health and Nutrition Examination Survey. Hyattsville, MD: Author.
11. Thompson, D. C.; Rivara, F. P.; and Thompson, R. S. (1996). “Effectiveness of Bicycle Safety Helmets in Preventing Head Injuries—A Case-Control Study.” Journal of the American Medical Association 276: 1968–1973.