Medical Decision Making and Demand

Introduction

Ever since medicine has been practiced, medical decision making has been conceptualized. Informal and formal rules have been in place to guide physicians in the therapeutic process – the Hippocratic Oath is a very early example. Probably up until the late nineteenth century the patient had little say in the physician’s decision making, and a rather paternalistic relationship between the two prevailed.

The twentieth century brought two important developments. First, the recognition of informed consent as a fundamental ethical requirement strengthened the patient’s role in the decision making process. Patients today are frequently characterized as responsible clients and customers who make informed decisions. Second, medical decision making was formalized and its scope extended beyond the direct patient–physician relationship, for example, to questions of public health and reimbursement.

Nowadays, the term medical decision making refers to a wide range of decisions in health care, with a special focus on the methods applied in the decision making process. The point of view from which such analyses are conducted can vary and includes the perspective of an individual physician or patient as well as the perspective of the policy maker. As the concern here is with the relationship between decision making and demand, the natural perspective is the patient’s.

Depending on one’s point of view, the criteria for assessing decision outcomes may differ and different theories and analytical methods may be applied. The field of medical decision making is characterized by a strong quantitative focus and covers a range of aspects from health economic evaluation to the analysis of cognitive processes and psychological factors. This article adheres to a very narrow definition of medical decision making, focusing on the role of formal decision analysis. This is well-suited to the fundamental concepts of health economics, which rely strongly on utilitarian principles.

Medical decision making and the analysis thereof is driven by the fact that decisions in medical care are in most cases characterized by two attributes: A varying, but frequently high degree of uncertainty and the availability of more than one alternative. Uncertainty arises from a number of sources. First of all, the onset of illness is a seemingly random event and can hardly be predicted. Furthermore, the presence of a sickness in a patient is uncertain; hence the decision maker faces a diagnostic risk. Then there is the therapeutic risk, as there is un-certainty over the effects of a specific therapy on a particular patient. At the same time, the patient himself knows neither how his body will react to the medication prescribed nor how the individual risk factors his genetics expose him to play into it. Another source of uncertainty is the fallibility of diagnostic tests, introducing the possibility of error at this stage of the treatment process.

Medical Decision Making

Basic Model

A formal analysis of medical decision making can help structure very complex problems. The structure of decision processes are typically represented by decision trees in which probabilities, outcomes, and sometimes other parameters are formalized and quantified. This makes all assumptions explicit and enables decision makers to draw informed conclusions. The aim is to identify the treatment strategy which yields the highest expected utility. Decision analysis is thus merely a tool for making informed decisions – the decision itself is still up to the decision maker, who decides how utility is defined and which components are taken into account. This means that legal, ethical, and professional considerations as well as patient preference and other factors can have an influence. The contribution of formal decision analysis is to provide structure, explicitness, and quantitative measures in this process and thereby facilitate an informed discussion (cf. Weinstein et al., 1980).

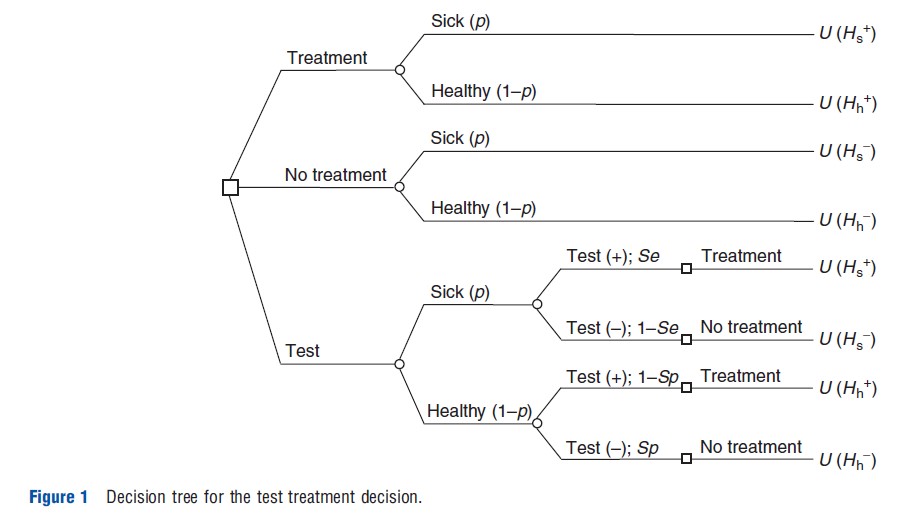
A basic model of medical decision making is developed, beginning with the decision over medical treatment under diagnostic risk. For simplicity, there is no differentiation between physicians and patients as decision makers in this model, but rather the assumption that physicians decide purely in the interest of their patients. The patient’s health state H_i is unknown; one can be sick or healthy, i=s, h. p describes the a priori probability of the sick state. The decision maker must decide whether to treat the patient (j=+) or not (j=- ). U(H^j_i) is the utility function which values health in its different possible states. Expected utility as a function of the treatment decision j becomes

The decision maker can also use diagnostic tools and make the treatment decision dependent on the test outcome, i.e., treat if the test is positive and not treat if it is negative. Therefore, j, j=+,-, is used, for the test outcome as well as the treatment decision. It follows that H_h^– indicates the health state after a true negative test result and H_h⁺ the health state after a false positive test result, whereas H_s⁺ stands for the health consequences of a true positive test result and H_s^– for those of a false negative test result.

The expected utility of a diagnostic test, EU^Dx(p), can then be written as follows:

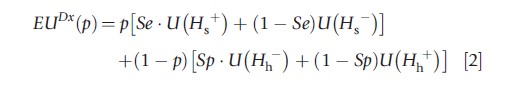
where ‘Se’ is the sensitivity or true positive rate, 1-Se is the false negative rate, ‘Sp’ is the specificity or true negative rate, and 1-Sp is the false positive rate of the test.

The decision tree in Figure 1 illustrates the decision maker’s choice. Squares represent decision nodes and circles indicate chance nodes.

It is useful to define:

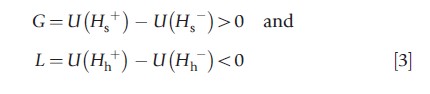
as the decision maker’s utility gain from treatment in the sick state and one’s utility loss from treatment in the healthy state.

Three threshold probabilities can now be derived at which the decision maker is indifferent between two actions, as introduced by Pauker and Kassirer (1975, 1980):

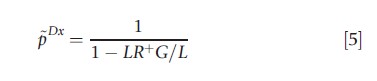
and

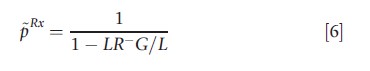
where LR⁺=Se/(1-Sp) denotes the positive and LR^–= (1-Se)/Sp the negative likelihood ratio of the test. LR⁺>1 and 0≤LR^– <1 holds for useful tests (i.e., Se+Sp>1).

The first threshold p~ is called the therapeutic threshold, at which the decision maker is indifferent between treating and not treating the patient in a situation where no diagnostic test is available. At the test threshold, p^Dx , one is indifferent between not treating and testing (followed by the treatment decision depending on the test outcome). At the treatment threshold, p^Rx , the decision maker is indifferent between testing and treating without prior testing. Because LR⁺>1>LR^–>0 and -G/L>0, p^Dx is located below the therapeutic threshold and p^Rx above it: ^pDx<p<p^Rx.

These thresholds allow us to characterize the decision maker’s optimal test and treatment strategy. At low a priori probabilities of sickness, 0≤p≤p^Dx , the optimal decision is not to use the test and not to treat. The dominant aspect in this situation is the utility loss resulting from a false positive test result. At intermediate a priori probabilities of sickness, p^Dx<p<p^Rx, the optimal strategy is to test and then to treat if the test outcome is positive. With a negative test outcome not treating is indicated. Finally, at high a priori probabilities, p^Rx <p<1, not testing is optimal and immediate treatment is indicated. The utility loss stemming from a false negative test outcome is the dominant factor here.

The Value Of Information

Medical decisions often involve the use of diagnostics. The optimal use of the information gleaned can be conceptualized using the value of information as introduced by Gould (1974). The value of diagnostic information is defined as the additional expected utility resulting from the use of the test. This requires considering the optimal decision when no test is available. This reference situation is characterized by the expected utility of not treating at p<p and the expected utility of treating at p≥p. Given eqns [1]–[3], we can solve for the value of information of a diagnostic test and find

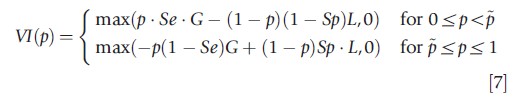
Figure 2 shows the value of information and the three thresholds discussed above. The value of information is positive between the test and treatment thresholds and reaches its maximum at the therapeutic threshold. At a priori probabilities of sickness below the test threshold or above the treatment threshold the value of information is zero: in these ranges the information technology should not be used in the treatment decision.

The value of information concept can be applied to situations in which several tests are available and the decision maker has to choose which one to use. It allows the evaluation of the decision maker’s marginal rate of substitution between sensitivity and specificity. The decision maker chooses the optimal test dependent on his preference and the given a priori probability of sickness.

Equation [7] leads to

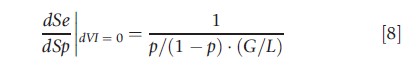
This equation was derived by McNeil et al. (1975) and Metz (1978), though without reference to the value of information concept. The marginal rate of substitution between sensitivity and specificity is decreasing in p. In other words, at high a priori probabilities of sickness the decision maker chooses a test with high sensitivity, whereas at low a priori probabilities one favors tests with high specificity. In the first situation, the benefits of treating the patient dominate, whereas in the second situation, the benefits of not treating become more relevant. The marginal rate of substitution is also decreasing in G/L. Hence, if either G increases or L decreases (in absolute terms), tests with high sensitivity are more attractive. Inversely, if either G decreases or L increases (in absolute terms), tests with high specificity are favorable.

Risk Aversion

Medical decision analysis often implicitly assumes a decision maker to be risk neutral. This is consistent with the practice of measuring intervention outcomes in terms of changes in mortality. New research also investigates the effect of higher order risk preference on medical decision making. Consider the effect of risk aversion on the test and treatment thresholds. For a decision maker with a concave utility function, i.e., marginal utility of health decreasing in the level of health, it is easy to show that G, the gain from treatment in the sick state, increases and L, the loss from treatment in the healthy state, decreases in absolute terms as compared to a decision maker with linear utility. With this, the decision maker’s test and treatment thresholds decrease (all p are decreasing in (-G/L)). Intuitively, if either the potential benefit from treatment increases or the potential harm decreases, the treatment option becomes more attractive. The risk averse decision maker uses his test and treatment strategy as an insurance device (it reduces the spread between the possible health states) by opting for testing and treatment at lower prevalence rates than a risk neutral decision maker. In situation where the decision maker can choose between several tests he will tend to favor those with high sensitivity if he is risk averse. This can be seen in eqn [8] because the marginal rate of substitution between sensitivity and specificity is increasing in (-G/L).

The decision maker’s risk preference are only partially described by risk aversion. Higher-order attitudes such as prudence and temperance also appear to play a role in decision making under uncertainty (Kimball, 1990; Eeckhoudt and Schlesinger, 2006). Felder and Mayrhofer (2013) analyze higher-order risk preference in a medical setting by adding a comorbidity risk to a specific index condition, or primary illness. They show that the effects of risk aversion on the test and treatment thresholds are reinforced when prudence and temperance are taken into account. Risk attitudes may explain why screening activities in very low a priori probability ranges are observed (for instance, the prostate-specific antigen (PSA)test for prostate cancer in asymptomatic middle-aged men) where under risk neutral decision making would not be expected.

The above example covers some of the basic concepts of formal decision analysis in the context of medical decision making. The focus is exclusively on the utility derived from the patient’s health status. (The utility of health states is often quantified and thus made comparable across illnesses by means of the quality-adjusted life-years concept.) Depending on the aim of the analysis the model will incorporate further information, for example, relating to treatment costs. The analysis can also pertain to a supply rather than a demand decision. In the following, we elaborate on a model which puts a stronger focus on the patient’s perspective and his demand for medical care.

Health Care Demand

Medical decision making can be integrated into a conventional demand framework. So far the gain from treatment, i.e., h=H_s⁺– H_s^–, was exogenous to the decision model. However, the effect of a treatment depends on the type and amount of medical inputs M that are used. A health production function h = f(M) describes this relationship.

The utility maximizing decision maker faces a limited budget, which he can spend on medical inputs M or on other consumption goods C. The utility function is thus U(C,H), which is strictly positive and strictly increasing in both M and C. Marginal utility is decreasing, implying that the individual is risk averse. To ensure that a change in consumption does not have an effect on the marginal utility of medical inputs and vice versa, the mixed derivatives must be zero.

To include h – the health gain produced by medical inputs – explicitly in the utility function, H=H_s^–+ h is noted. (To keep this illustration simple, healthy patients and the potential issues they raise are disregarded.) The utility function can then be written as

Demand for health services now becomes a derived demand, as it is driven by the underlying demand for health. All prices except for medical inputs are set equal to one. With income Y, the budget constraint is

Solving the Lagrangean function L(C,M,λ)=(C,H_s^–+f (M))+λ(C+p_MM-Y), where l indicates the marginal utility of income, a combined first-order condition is derived for the utility maximizing demand for consumption and health care:

The right side of the equation can be interpreted as the marginal cost of investing in health. By rewriting this equation the following equation is obtained:

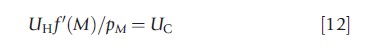
which can be interpreted intuitively: In the optimum, the last monetary unit spent must generate the same marginal utility whether it is spent on medical care or on consumption.

Conducting a comparative static analysis can investigate the effects of changes in the exogenous variables on the demand for health. Let us first look at technological innovation and assume that h=φM^a, where φ>0 reflects the productivity parameter. If innovation increases the productivity of medical inputs, this is reflected in an increase in the marginal product of medical inputs φ`(M)=φaM^a-1. In other words, the marginal cost of producing health diminishes. This results in higher demand for health and medical inputs. The opposite effect is caused by higher prices for medical inputs. Although higher income also results in a higher level of demand, a higher initial health level does not have a clear positive or negative effect. In this model, the probability of survival, which is included in the expected utility function, has no influence on demand.

This model can be extended to include the aspect that health care demand is often directed toward preventing early death. A simple approach to modeling survival is to introduce an initial probability of survival π₀ which can be increased by medical inputs: π(M)π₀+g(M) with g`(M)>0 and g“(M)<0. This extension permits the evaluation of the demand for health as a function of initial survival. It can be shown (see Felder and Mayrhofer (2011)) that the demand for health care is inversely related to the initial survival rate, which is tantamount to the famous dead-anyway effect (Pratt and Zeckhauser, 1996).

Double Moral Hazard Under Two-Sided Asymmetric Information

This article began by outlining a basic model of medical decision making which assumes that the physician acts as a perfect agent for the patient. In the second model the focus was on the patient’s view. In practice, both perspectives have to be combined. A primary reason is that patients have become increasingly involved in treatment decisions. They want to participate in the decision making process and physicians want them to understand the implications of the decisions that have to be taken. Second, even disregarding an ideal-type shared decision making process, the outcomes for physicians and patients are interlinked.

A model that characterizes this relationship must also map out the underlying two-way moral hazard structure. A simplified model would contain only one stage, in which a utility maximizing physician makes a treatment decision based on factors such as the patient’s health status, coinsurance, and his remuneration. However, the health outcome depends not only on the treatment, but also on the patient’s health-related behavior, even beyond the narrowly defined notion of compliance. This creates strategic interdependence between the levels of utility realized by the physician and the patient. Both sides suffer from information deficits. The patient either does not know whether the physician is sharing all relevant information or simply lacks the capability to understand all the information that is given. Furthermore, they cannot easily verify the quality of the treatment. On the other side, the physician does not know everything about the patient’s health-related behavior. This behavior, however, affects the health outcome. Thus, health outcomes can be interpreted as the result of both the physician’s medical services and the patient’s behavior.

The physician’s treatment decision and the patient’s health-related behavior can interact in three key ways: Medical services and health behavior can be strategically independent, implying that the level of medical services does not affect the marginal productivity of the patient’s compliance and vice versa. Alternatively, the two components can be strategic complements, i.e., if one factor is increased this has a positive effect on the other factor. Finally, they might be strategic substitutes, so that a lower level of health care services can be compensated – at least so some extent – by better health-related behavior. These three types of interaction between physician decision and patient behavior yield different results. There is some evidence that there is indeed a strong mutual influence of the demand for health and the provision of health care services (Schneider and Ulrich, 2008).

Concluding Remarks

The expected utility theory of von Neumann and Morgenstern is the fundamental building block of most models in medical decision making under uncertainty. However, it has been criticized for its failure to predict individual behavior. Alternative non-expected utility theories such as rank-dependent choice models have been suggested to reflect actual behavior more precisely. One aspect, for instance, is that decision makers tend to overweight small probabilities and underweight large probabilities, which leads to an inverse S-shaped probability transformation which has been confirmed in empirical studies (Abdellaoui, 2000; Bleichrodt and Pinto, 2000).

Recent research, in turn, has challenged the validity of rank-dependent theory. Among others, List (2004) showed that individuals with extensive experience behave largely rationally, or in accordance with the expected utility theory. Physicians take decisions on tests and treatments as a matter of routine – and they are expected to make unbiased estimations of probabilities and take coherent decisions.

The use of the expected utility theory is also warranted in the prescriptive realm of medical decision making. If an optimal policy has to be chosen or recommended, ‘‘the expected utility is the best theory to determine which decisions to undertake’’ (Wakker, 2008, p. 687).

Bibliography:

1. Abdellaoui, M. (2000). Parameter-free elicitation of utility and probability weighting functions. Management Sciences 46(11), 1497–1512.
2. Bleichrodt, H. and Pinto, J. L. (2000). A parameter-free elicitation of the probability weighting Functions. Management Sciences 46(11), 1485–1496.
3. Eeckhoudt, L. and Schlesinger, H. (2006). Putting risk in its proper place. American Economic Review 96, 280–289.
4. Felder, S. and Mayrhofer, T. (2011). Medical decision making, a health economic primer. Heidelberg: Springer.
5. Felder S. and Mayrhofer T. (2013). Higher-order risk preference: Consequences for test and treatment thresholds and optimal cutoffs. Medical Decision Making (in press).
6. Gould, J. P. (1974). Risk, stochastic preference, and the value of information. Journal of Economic Theory 8(1), 64–84.
7. Kimball, M. S. (1990). Precautionary saving in the small and in the large. Econometrica 58(1), 53–73.
8. List, J. (2004). Neoclassical theory versus prospect theory: Evidence from the market place. Econometrica 72(2), 615–625.
9. McNeil, B. J., Keeler, M. and Adelstein, S. M. (1975). Primer on certain elements of medical decision making. New England Journal of Medicine 293(5), 211–215.
10. Metz, C. E. (1978). Basic principles of ROC analysis. Seminars in Nuclear Medicine 8(4), 283–298.
11. Pauker, S. G. and Kassirer, J. P. (1975). Therapeutic decision making: A cost benefit analysis. New England Journal of Medicine 293(5), 229–234.
12. Pauker, S. G. and Kassirer, J. P. (1980). The threshold approach to clinical decision making. New England Journal of Medicine 302(20), 1109–1117.
13. Pratt, J. W. and Zeckhauser, R. J. (1996). Willingness to pay and the distribution of risk and wealth. The Journal of Political Economy 104(4), 747–763.
14. Schneider, U. and Ulrich, V. (2008). The physician-patient relationship revisited: The patient’s view. International Journal of Health Care Finance and Economics 8(4), 279–300.
15. Wakker, P. P. (2008). Lessons learned by (from?) an economist working in medical decision making. Medical Decision Making 208, 690–698.
16. Weinstein, M. C., Fineberg, H. V., Elstein, A. S., et al. (1980). Clinical decision analysis. Philadelphia: W.B. Saunders.