Measuring Equality and Equity in Health

Introduction

Health economics is a relatively young sub discipline, and the measurement of inequalities in the health domain has only relatively recently received attention from health economists. Nevertheless, and perhaps unsurprisingly, the topic has a very long history outside health economics, in particular in public health, demography, sociology, and epidemiology. The notion of a ‘gradient in health’ across measures of socioeconomic status has been the subject of empirical analysis and speculation regarding its causes for more than a century. For example, in the mid-nineteenth century, William Farr proposed a law relating mortality with population density. At around this time, the famous political economist William Stanley Jevons examined variation in the rate of mortality in different English cities, attributing differences to the proportion of poor Irish immigrants (Jevons, 1870). In the early part of the twentieth century, there were also several empirical examinations of income-related gradients in mortality, including analyses by Hibbs (1915) and Woodbury (1924) of the gradient in infant mortality in the US using information collected from household surveys. A key issue then (as now) was whether the relationship between health and income was purely a correlation, or implied some form of causation. However, most of these early studies reported the health–income gradients only in a tabular or graphical form and did not apply any of the measures the authors examine here.

In this article, the authors give a nonexhaustive overview of the techniques that economists have developed to measure inequality and inequity in health and health care. These measures have their origins in univariate measures such as the Gini coefficient and the Lorenz curve that were developed in the early twentieth century to measure income inequality. Economists also developed bivariate inequality measures, particularly for quantifying the distribution of categories of expenditure across income (Wis´niewski, 1935). Some of these early studies used measures such as concentration curves and indexes to examine health care spending as a component of household expenditure at different levels of income (Iyengar, 1960; Ghezelbash, 1963).

It has only been in the past few decades that these measures have been used specifically for health economics applications. Probably the first proposal for the use of the Gini coefficient in a health economics context can be attributed to Chen (1976), who formulated the K index as a proxy measure of health care quality. The rationale for using this measure was as a way of penalizing situations where avoidable morbidity was concentrated in a small number of individuals rather than being spread more evenly across a community. Le Grand (1987) also applied the Gini coefficient to quantify inequalities in age at death in his international comparisons across a range of high and middle income countries. However, more recent applications of the Gini are less common than studies focusing on bivariate inequality, i.e., the correlation between health and measures of socioeconomic status such as income. Here, the measure traditionally adopted is the concentration index, stemming from proposals of Wagstaff et al. (1991), which has been widely employed in international inequality comparisons (e.g., see Van Doorslaer et al., 1997). In the past few years, there has been a considerable interest in developing new uniand bivariate health inequality measures, in part to address some of the aspects of health such as the bounded nature of many health measures (e.g., rates of mortality must fall in the 0–1 range).

The authors’ overview focuses on the most important contributions since 2000 and is intended primarily as a catalog of what is available at present. They therefore confine themselves to a short presentation of the various measurement techniques developed by economists; for more in-depth discussions or the literature on the causal mechanisms linking health and income the authors refer to the literature list at the end of this article. The remainder of this article contains four sections. The authors discuss the measurement of inequality in the next section. Next, the authors deal with decomposition methods and introduces methods to measure health inequities. The final section concludes. For brevity, the authors refer to health variables in what follows, but all methods described in this article can be applied to any variable measuring health, health care use, and health care expenditures.

Measurement Of Inequality

Measurement Of Total (I.E., Univariate) Health Inequality

The initial focus of this article is measurement of the degree of inequality within a given health distribution. The literature on the measurement of this type of health inequality borrows heavily from the literature on the measurement of income inequality.

Throughout this article, the authors consider a population of n individuals that are ranked by their health levels, i.e., each individual i = 1,…, n is characterized by a health level h_i and h₁≤h₂≤…≤h_n. They always assume that the health variable h_i has a well-defined, finite lower bound h^min. With regard to the upper bound, they distinguish between the infinite and finite case, i.e., the authors have either h_iϵ[h^min,+∞] or h_iϵ[h^min, h^max]. When the health variable is of the ratio-scale type, they assume that h^min = 0.

For ratio-scale variables with an infinite upper bound, the most popular inequality indicator is the Gini index, which can be written as a weighted sum of health shares (Lambert, 2001):

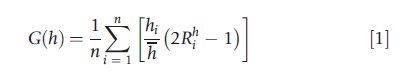
where h denotes average health and Rh is the fractional rank of individual i (in the absence of ties we have R^h_i=(i-0.5)/n; in the presence of ties the definition is slightly different). The Gini index is a relative inequality index: it focuses on the relative health differences between individuals. If one wants to stress the absolute differences between individuals, one could use the generalized Gini index, which is an absolute inequality index obtained by multiplying the Gini index by average health:

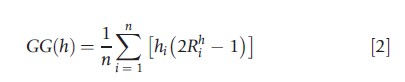
In principle, any relative or absolute inequality index used for the measurement of income inequality can also be used for the measurement of health inequality. But there is an important caveat: because the health variable is not necessarily of the ratio-scale type, one should not take for granted that indicators developed for ratio-scale variables generate meaningful information when applied to other types of variables, such as nominal, ordinal, or cardinal health variables. Depending on the nature of the variable, different inequality indicators are called for. For instance, Abul Naga and Yalcin (2008) have derived a class of indicators tailored to measure inequality for ordinal health variables.

The situation also changes when the health variable has a finite upper bound, for example, a maximum value of 100%. In that case, one can look either at attainment levels, measured by the health variable hi, or at shortfall levels, measured by the ill-heath variable s_i=h^max-h_i. Recent publications (Erreygers, 2009b; Lambert and Zheng, 2011) have explored what this implies for health inequality measurement. These studies start from the idea that the attainment and shortfall indicators should be complementary, which in its strongest form imposes that attainment inequality is always equal to shortfall inequality. As far as the Gini family is concerned, the strong complementarity criterion leads to the following corrected version of the Gini indicator (Erreygers, 2009b):

A similar correction can be applied to the coefficient of variation family. As shown by Lambert and Zheng (2011), the combination of a weak version of complementarity and decomposability points in the direction of the variance as a measure of inequality.

Measurement Of Socioeconomic Health Inequality

The dominant strand in the health inequality literature deals with bivariate inequality, and focuses on the correlation between health and socioeconomic status. The most popular measure in this field is the concentration index. Suppose that y_i is a variable which measures the socioeconomic status of individuals; this variable can be occupation, education, income, wealth, etc. Let R^y_t be the fractional rank of an individual according to the chosen socioeconomic variable. The concentration index can be written as (Wagstaff et al., 1991):

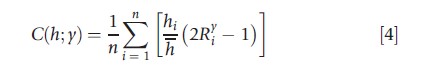
Observe that the socioeconomic variable need not be of the ratio-scale type; the index only requires information on the socioeconomic rank, which can also be obtained from an ordinal variable.

Different variants of the standard concentration index C(h;y) have been introduced over the years. If one wants to focus on absolute, rather than relative, health differences between individuals, one can use the generalized concentration index GG(h;y)=hC(h;y). It is also possible to express different degrees of sensitivity to inequality by using the extended concentration index (Wagstaff, 2002). Again, the authors have a different story when they are dealing with bounded health variables (Clarke et al., 2002). The counterpart of the strong complementarity criterion, which the authors mentioned in the previous subsection, is the ‘mirror’ condition. This requires that the measured degree of socioeconomic inequality of health should be the reverse of the measured degree of socioeconomic inequality of ill health. Recently, two indicators, which satisfy the mirror condition, have been suggested. The first (Wagstaff, 2005) is defined as:

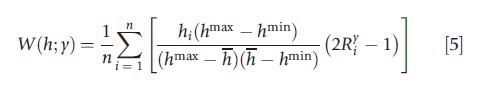
and the second (Erreygers, 2009a) as:

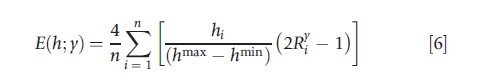
Because both have the mirror property, the level of socio-economic inequality in health and ill health is identical, except for the sign, i.e., W(h; y) = -W(s; y) and E(h; y) = – E(s; y), but in other respects the indices are very different. Erreygers and Van Ourti (2011) provide an in-depth discussion of the properties of these two indicators, in the context of a more general examination of the applicability of rank-dependent indicators.

Decomposition Methods

In the previous sections Measurement of Inequality, the authors covered the most popular inequality indices in the health economics literature. These indices have frequently been used to compare inequality levels between countries or within countries over time but do not allow to infer what lies behind these differences in (socioeconomic) inequality. Decomposition methods – first developed in labor economics and in the income inequality literature – are a useful tool to align the analysis more with an explanatory approach.

Factor Decompositions

Wagstaff et al. (2003) were the first to highlight the usefulness of applying existing decomposition methods to the health domain, in particular to the concentration index. When health can be written as a linear function of K factors (e.g., socioeconomic status, demographics, lifestyles, …), one can express socioeconomic health inequality as a weighted sum of the socioeconomic inequalities in these factors. This is most easily seen from combining eqn [4] with a regression model that associates health linearly to K factors x_ik:

where a and β₁,β₂,…,β_K are coefficients and ε_i an error term with zero mean. After some algebra, the following result emerges:

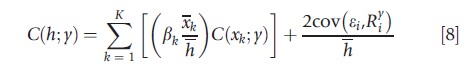
which shows that socioeconomic health inequality is affected (a) by the magnitudes of the impact of the K factors on health – measured by the average elasticities β_kx_k/h – and (b) by the socioeconomic inequalities in each of the contributing factors – measured by the concentration indices C(x_k; y). There is also a residual term summarizing the covariance between the error term of eqn [7] and the fractional socioeconomic rank. Similarly, one can derive decompositions of the other univariate and bivariate indices discussed in the previous sections Measurement of Inequality. The authors refer interested readers to O’Donnell et al. (2006), Erreygers (2009a) and Van Doorslaer and Van Ourti (2011). Readers interested in subgroup decompositions should consult Clarke et al. (2003).

Longitudinal Decompositions

A factor decomposition unravels the link between (socioeconomic) health inequality and its associated factors, but in many occasions the authors are interested in the difference between two inequality indices. They now describe decompositions of the change of (socioeconomic) health inequality over time. Note that many of these methods can also be used to decompose differences between countries.

Wagstaff et al. (2003) describe an Oaxaca–Blinder decomposition of the change in the concentration index that starts from eqn [8]. It reveals whether changes in (socioeconomic) health inequality are mainly driven by changes in socioeconomic inequalities in the associated factors x_k or by changes in the associated elasticities η_k.

where ∆C denotes the difference between two concentration indices in period t and l; and REST is a residual term.

Van Ourti et al. (2009) have adapted the Oaxaca–Blinder decomposition in eqn [9] in order to reveal the relation between the change in income-related health inequality, income growth, and the change in income inequality. This decomposition starts from eqn [7] but allows for a nonlinear association between income (included in x_k) and health. The health elasticity of income turns out to play a crucial role; if this elasticity is increasing with income, then proportional income growth will lead to higher income-related health inequality, and vice versa.

Allanson et al. (2010) have recently developed a related longitudinal decomposition that extends the work of Jones and Lopez Nicolas (2004). Jones and Lopez Nicolas (2004) study concentration indices based on short-run (cross-section) and long-run (panel averages) measures of health and socioeconomic status using insights from the literature on income mobility (Shorrocks, 1978), and show they diverge when there are systematic differences in health between those whose socioeconomic status is upwardly and downwardly mobile. An important trademark of their decomposition is that it allows to show whether socioeconomic health inequalities are persistent over time. However, it cannot illustrate whether health changes are more/less pronounced for those with high relative to low socioeconomic status. Allanson et al. (2010) show that the change in socioeconomic health inequalities can be written as the sum of ‘socioeconomic health mobility’ (i.e., the extent to which health changes accrue to those with an initial high relative to low socioeconomic status) and ‘health-related socioeconomic mobility’ (i.e., the extent to which socioeconomic status changes are larger/smaller for the initially healthy or unhealthy). The same authors have also studied the effects of deaths in longitudinal decompositions (Petrie et al., 2011).

Measurement Of Inequity

Until now, the discussion has been mainly confined to ways of measuring and decomposing (socioeconomic) health inequality. Although this is totally in line with having ‘the numbers tell the tale’, it is not clear whether society at large is concerned about all (socioeconomic) health inequalities. It seems highly plausible that people are concerned about some causes/drivers of inequalities, but less about others. The former is usually denoted as inequity and is the focal point of this section.

Measurement Of Horizontal Inequity

The dominant inequity concept is that of horizontal inequity, which states that equals should be treated equally. The concept of vertical equity – which states how unequally unequals should be treated – is as important, but has received far less attention in the literature due to empirical difficulties to estimate the vertical equity norm (Sutton (2002) is a noteworthy exception).

When measuring horizontal socioeconomic inequity in health, one should start by defining whether variation in health attributable to certain factors is equitable or inequitable. The typical stance in the literature is to consider the variation due to age and sex as equitable and all other variation as inequitable. This is much in line with the practice of standardizing health for age and sex that is popular in public health and epidemiology, but in principle the subdivision between equitable and inequitable health variation allows for a broad range of value judgments (including e.g., the case where equality of health outcomes is inequitable). Two procedures have become popular in the health economics literature (Wagstaff and Van Doorslaer, 2000; Gravelle, 2003; Fleurbaey and Schokkaert, 2009). The first, denoted ‘direct standardization’, boils down to calculating the predicted value of eqn [7] keeping those factors that lead to equitable health variation fixed (e.g., fixing age and sex at a specific value). The resulting index of socioeconomic inequity HI^dir(h; y) calculates the socioeconomic inequality in these predicted health values:

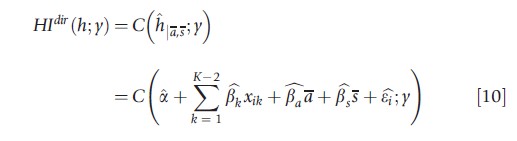
where ^ denotes an estimate, and age and sex have been fixed at their average values a and s. The second approach, ‘indirect standardization’, boils down to calculating the difference between the actual socioeconomic inequality in health and the hypothetical situation where socioeconomic inequality reflects only variation due to equitable variables (which is obtained by fixing the values of the variables that lead to inequitable health variation in eqn [7]):

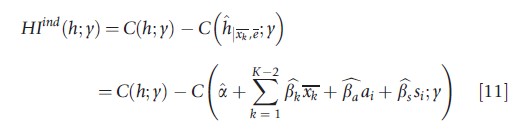
where the inequitable variables and the error term are fixed at their average values x_k and 0.

The horizontal inequities obtained from eqns [10] and [11] are similar because eqn [7] is linear. Owing to the linearity of eqn [7], it is also straightforward to see that there is an exact link between the factor decomposition of the concentration index and indices of horizontal inequity: in other words, by rearranging the decomposition in eqn [8] – i.e., moving the contributions of age and sex to the left hand side – eqns [10] and [11] are obtained. However, in many empirical applications a nonlinear functional form is preferred for eqn [7] due to the skewed distribution of health. In the latter case, the exact link with the decomposition in eqn [8] is lost, but as long as the variables leading to equitable and inequitable health variation are additively separable, eqns [10] and [11] are still similar. When additive separability no longer holds – which occurs, for example, when the health effect of medical supply (an inequitable variable in our example) depends on the age of the individual (an equitable variable) – eqns [10] and [11] will give different estimates of horizontal inequity. In the next section, the authors discuss this difference in a more general setting and highlight the ethical positions underlying the indirect and direct standardization procedures.

Methodology Of Fleurbaey And Schokkaert (2009): Insights From Social Choice

In this section, the authors very shortly introduce a recent contribution to the literature on health equity measurement that is not based on the concentration index. Fleurbaey and Schokkaert (2009) have discussed how the theory of fair allocation (Fleurbaey, 2008) – a social choice theory – could be used to measure health and health care inequities. The most important difference with approaches based on the concentration index (or other related rank-dependent inequality indices) is that it consists of a two-step approach. In the first step, the sole and ultimate goal should be to estimate the ‘best’ empirical model that links health to its determinants. In a second and independent step the inequities in health are measured, and the procedure is similar whether the underlying equation linking health and its determinants is linear, nonlinear, or not additively separable in the equitable and nonequitable variables. It boils down to subdividing the list of variables into those causing equitable and inequitable health variation (much like before), and next calculates all inequities related to the variables that lead to inequitable health variation. This is different from the methods based on the concentration index that focus on socioeconomic inequity only; and hence the theory of fair allocation allows the measurement of inequities along a broader spectrum of ethical stances.

The first step consists of modeling how health relates to its determinants, i.e., an exercise in pure positive economics. Preferably, a structural econometrics model that disentangles how determinants affect health directly and indirectly (via other endogenous variables such as income, medical care, lifestyles, and so on) is used, but in this section the authors stick to a reduced form to illustrate the most basic version of the approach of Fleurbaey and Schokkaert (2009):

where f(.) links health to the vector of regressors x_i.

Once f(.) has been estimated, the researcher (or the outcome of a public debate) should subdivide the vector of regressors into a set of variables that lead to equitable (x^eq_i) and inequitable health variation (xⁱⁿ_i ). Although the description is based on the reduced form in eqn [12], it should be clear that a structural model might be extremely useful in guiding the subdivision, as it allows the distinction of the direct and indirect effects of explanatory variables (e.g., think of a case where the indirect impact of gender on health via unhealthy behavior is considered equitable, whereas the direct impact of gender on health might be considered inequitable). The subdivision allows to introduce two concepts that have been developed in the theory of fair allocation and that are closely related to the two standardization approaches the authors introduced in previous section Measurement of Horizontal Inequity. ‘Direct unfairness’ is in the same vein as ‘direct standardization’ and proceeds by fixing the value of x^eq_i at a reference value h^dir_i=f(x^eq_i;xⁱⁿ_i). The alternative procedure compares actual health with a ‘fair’ distribution of health where xⁱⁿ_i is fixed, i.e., h^fg_i=h_i-f(x^eq_i;(xⁱⁿ_i)). Next, one calculates inequity in health by measuring inequalities in h^dir_i or h^fg_i. Fleurbaey and Schokkaert (2009) argue in favor of using an absolute inequality index.

Several things are worth pointing out. First, if socioeconomic status is considered as the only determinant leading to inequitable health variation, these methods conceptually coincide with the approach based on the concentration index; but as soon as other choices are made with respect to the subdivision of factors leading to equitable and inequitable health variation, both approaches will diverge. Second, the approach translates an inherently multidimensional problem into a one-dimensional inequality problem. In contrast, approaches based on the framework of concentration indices are multidimensional in nature. Third and similarly to the discussion of the two standardization procedures in the previous section Measurement of Inequality, the functional form of f (.) is crucial. When additive separability applies so that h_i=f(x_i)= g(x^eq_i)+h(xⁱⁿ_i) , inequalities in ‘direct unfairness’ and the ‘fairness gap’ are identical, but when this is not the case inequalities diverge. The theory of fair allocation can however guide the choice between ‘direct unfairness’ and the ‘fairness gap’. ‘Direct unfairness’ imposes that health differences due to factors leading to equitable health variation are not reflected in estimates of inequity, whereas the ‘fairness gap’ imposes that absence of inequity in health coincides with an absence of inequitable health variation. Both requirements seem plausible but cannot be jointly true when the function linking health to its determinants is not additively separable in the factors leading to equitable and inequitable health variation. For more discussion, the authors refer to Fleurbaey and Schokkaert (2009).

Conclusion

This article gives a nonexhaustive overview of techniques to measure inequality and inequity in health and health care. The authors have focused on the most important health economics contributions since 2000, but they have also acknowledged that this literature is embedded in a long tradition of research on the socioeconomic health gradient that dates back to more than a hundred years. In fact, the recent research can be seen as revival interest in bivariate as opposed to univariate measures of inequalities.

The first part of the article has dealt with the measurement of univariate inequalities in health. Special attention was paid to bounded health variables; and the implications for health inequality measurement. Next, the authors covered the concentration index and related indices that have been popular to measure bivariate socioeconomic health inequalities.

The second part of the article introduced decomposition methods that are useful to align the analysis more with an explanatory approach. The authors subsequently covered factor decompositions and longitudinal decompositions. The first allows the contribution of separate health determinants to health inequalities to be disentangled; the second is useful to understand what drives changes in health inequalities over time (or between countries) and whether it is always the same people in poor or good health.

In the final part of the paper the authors have moved from inequalities to inequities, i.e., that share of total inequalities that is found to be inequitable. They have covered the traditional approach in health economics that focuses on horizontal socioeconomic-related inequities; and introduced a new and promising approach – derived from social choice theory – that allows to calculate health inequities along a broad set of ethical positions.

Acknowledgments

Tom Van Ourti is supported by the National Institute on Ageing, under grant R01AG037398, and also acknowledges support from the NETSPAR project ‘Health and income, work and care across the life cycle II’. This article has benefited from the comments and suggestions of Ulf Gerdtham, Gustav Kjellson, and the editors. The usual caveats apply and all remaining errors are our responsibility.

References:

1. Abul Naga, R. H. and Yalcin, T. (2008). Inequality measurement for ordered response health data. Journal of Health Economics 27, 1614–1625.
2. Allanson, P., Gerdtham, U. -G. and Petrie, D. (2010). Longitudinal analysis of income-related health inequality. Journal of Health Economics 29, 78–86.
3. Chen, M. K. (1976). The K index: A proxy measure of health care quality. Health Services Research 11, 452–463.
4. Clarke, P., Gerdtham, U., Johannesson, M., Bingefors, K. and Smith, L. (2002). On the measurement of relative and absolute income-related health inequality. Social Science & Medicine 55, 1923–1928.
5. Clarke, P. M., Gerdtham, U. -G. and Connelly, L. B. (2003). A note on the decomposition of the health concentration index. Health Economics 12, 511–516.
6. Erreygers, G. (2009a). Correcting the concentration index. Journal of Health Economics 28, 504–515.
7. Erreygers, G. (2009b). Can a single indicator measure both attainment and shortfall inequality? Journal of Health Economics 28, 885–893.
8. Erreygers, G. and Van Ourti, T. (2011). Measuring socioeconomic inequality in health, health care, and health financing by means of rank-dependent indices: A recipe for good practice. Journal of Health Economics 30, 685–694.
9. Fleurbaey, M. (2008). Fairness, responsibility, and welfare. Oxford: Oxford University Press.
10. Fleurbaey, M. and Schokkaert, E. (2009). Unfair inequalities in health and health care. Journal of Health Economics 28, 73–90.
11. Ghezelbash, A. (1963). The urban consumer survey and income elasticities in Iran. Review of Income and Wealth 1963, 168–176.
12. Gravelle, H. (2003). Measuring income related inequality in health: Standardisation and the partial concentration index. Health Economics 12, 803–819.
13. Hibbs, H. H. (1915). The influence of economic and industrial conditions on infant mortality. Quarterly Journal of Economics 30, 127–151.
14. Iyengar, N. S. (1960). On a method of computing Engel elasticities from concentration curves. Econometrica 28, 882–891.
15. Jevons, W. S. (1870). Opening address of the President of section F (Economic Science and Statistics), of the British Association for the Advancement of Science, at the fortieth meeting, at Liverpool. Journal of the Statistical Society of London 33, 309–326.
16. Jones, A. M. and Lpez-Nicols, A. (2004). Measurement and explanation of socioeconomic inequality in health with longitudinal data. Health Economics 13, 1015–1030.
17. Lambert, P. (2001). The distribution and redistribution of income (3rd ed.). Manchester: Manchester University Press.
18. Lambert, P. and Zheng, B. (2011). On the consistent measurement of attainment and shortfall inequality. Journal of Health Economics 30, 214–219.
19. Le Grand, J. (1987). Inequalities in health: Some international comparisons. European Economic Review 31, 182–191.
20. O’Donnell, O., van Doorslaer, E. and Wagstaff, A. (2006). Chapter 17: Decomposition of inequalities in health and health care. In Jones, A. (ed.) The elgar companion to health economics, pp. 179–192. Cheltenham: Edward Elgar.
21. Petrie, D., Allanson, P. and Gerdtham, U. (2011). Accounting for the dead in the longitudinal analysis of income-related health inequalities. Journal of Health Economics 30, 1113–1123.
22. Shorrocks, A. (1978). Income inequality and income mobility. Journal of Economic Theory 19, 376–393.
23. Sutton, M. (2002). Vertical and horizontal aspects of socio-economic inequity in general practitioner contacts in Scotland. Health Economics 11, 537–549.
24. Van Doorslaer, E. and Van Ourti, T. (2011). Chapter 35: Measuring inequality and inequity in health and health care. In Smith, P. and Glied, S. (eds.) The Oxford handbook of health economics, pp. 837–869. Oxford: Oxford University Press.
25. Van Doorslaer, E., Wagstaff, A., Bleichrodt, H., et al. (1997). Income-related inequalities in health: Some international comparisons. Journal of Health Economics 16, 93–112.
26. Van Ourti, T., van Doorslaer, E. and Koolman, X. (2009). The effect of income growth and inequality on health inequality: Theory and empirical evidence from the European panel. Journal of Health Economics 28, 525–539.
27. Wagstaff, A. (2002). Inequality aversion, health inequalities, and health achievement. Journal of Health Economics 21, 627–641.
28. Wagstaff, A. (2005). The bounds of the concentration index when the variable of interest is binary, with an application to immunization inequality. Health Economics 14, 429–432.
29. Wagstaff, A. and Van Doorslaer, E. (2000). Measuring and testing for inequity in the delivery of health care. Journal of Human Resources 35, 716–733.
30. Wagstaff, A., van Doorslaer, E. and Watanabe, N. (2003). On decomposing the causes of health sector inequalities with an application to malnutrition inequalities in Vietnam. Journal of Econometrics 112, 207–223.
31. Wagstaff, A., Paci, P. and van Doorslaer, E. (1991). On the measurement of inequalities in health. Social Science and Medicine 33, 545–557.
32. Wis´niewski, J. (1935). Demand in relation to the income curve. Econometrica 3, 411–415.
33. Woodbury, R. M. (1924). Economic factors in infant mortality. Journal of the American Statistical Association 19, 137–155.
34. Cutler, D. M., Lleras-Muney, A. and Vogl, T. (2011). Chapter 7: Socioeconomic status and health: Dimensions and mechanisms. In Smith, P. and Glied, S. (eds.) The Oxford handbook of health economics, pp. 124–163. Oxford: Oxford University Press.
35. Fleurbaey, M. and Schokkaert, E. (2011). Equity in health and health care. In Pauly, M. V., McGuire, T. and Barros, P. P. (eds.) Handbook of health economics, Vol. 2, pp. 1003–1092. Amsterdam: North Holland.
36. Gravelle, H., Morris, S. and Sutton, M. (2006). Economic studies of equity in the consumption of health care. In Jones, A. (ed.) The elgar companion to health economics, pp. 193–204. Cheltenham: Edward Elgar.
37. O’Donnell, O., van Doorslaer, E., Wagstaff, A. and Lindelo¨w, M. (2008). Analyzing health equity using household survey data: A guide to techniques and their implementation. Washington DC: The World Bank.
38. Wagstaff, A. and van Doorslaer, E. (2000). Equity in health care finance and delivery. In Culyer, A. and Newhouse, J. P. (eds.) Handbook of health economics, Vol. 1, pp. 1803–1862. Amsterdam: North Holland.