Introduction
As a vehicle for economic evaluation, model-based cost-effectiveness analysis offers major advantages over trial-based analysis. These include the facility of models to widen the set of options under comparison and to incorporate all relevant evidence. To achieve these, appropriate clinical evidence needs to be indentified and synthesized, particularly that relating to treatment effects on relevant endpoints. Meta-analysis is the field of clinical epidemiology, which focuses on evidence synthesis. Recent method development in this field has focused on the particular needs of economic evaluation to incorporate all the relevant evidence relating to all management options.
Limitations Of Pairwise Meta-Analysis
Meta-analysis is the process of using statistical techniques to synthesize the results from separate but related studies in order to obtain an overall estimate of treatment effect. Traditionally, randomized clinical trials (RCTs) have been meta-analyzed by combining results or data from a series of trials comparing the same two treatments. This has been referred to as pairwise meta-analysis. This form of analysis has a number of limitations. For example, it may exclude trials that potentially provide indirect information regarding the treatment effect of interest. This may lead to it being impossible to estimate a treatment effect or to a potentially important information being excluded from the analysis. In addition, where there are more than two treatments of interest it can be hard to interpret the results and associated uncertainty of a series of separate pairwise comparisons, particularly where the results of the individual analyses appear to be contradictory.
Network Meta-Analysis
Network meta-analysis is an extension of pairwise meta-analysis that provides estimates of the relative effectiveness of two or more treatments derived from a statistical analysis of the data from a set of RCTs, where the trial comparisons form a connected network. The estimates of relative effectiveness, alongside estimates of uncertainty, based on a systematic synthesis of the available RCT evidence, are potentially an important component of medical decision-making.
Adjusted Indirect Comparison
The simplest form of network analysis has been referred to as an adjusted indirect comparison (AIC). In an AIC an indirect estimate of the average treatment effect between two treatments is estimated based on the results of RCTs that directly compare the two treatments of interest to a common comparator. It is adjusted in the sense that it allows for differences between trials in the response to the common comparator. Researchers have suggested the term ‘anchored indirect comparison’ as an alternative to adjusted indirect comparison to differentiate from those analyses in which covariable adjustment is included.
The indirect estimate is obtained by applying the constraint that δAB =δAC-δBC on the scale of analysis, where δAB is the indirect estimate of the effect of treatment A compared with treatment B, and δAc and δBC are the direct estimates of the effects of treatments A and B, respectively, compared with the common comparator treatment C.
For example, consider a binary outcome with the constraint that δAB=δAC -δBC on the log-odds scale. An indirect estimate of the log-odds ratio for treatment A compared with B (LORAB) can be estimated as LORAB=LORAC-LORBC , where LORAC and LORBC are estimates of the log-odds ratios obtained from single RCTs or from a meta-analysis of multiple RCTs. This is equivalent to ORAB=ORAC /ORBC , where OR refers to the odds ratios.
Estimating Uncertainty
The uncertainty in an adjusted indirect estimate can be estimated as the sum of the variances for each of the component direct estimates as these can be treated as independent random variables (coming from separate RCTs). For example, var(LORAB) =var(LORAC)+var(LOR+). The standard error and 95% confidence interval can then be derived from the variance estimate. It should be noted that estimates of uncertainty calculated in this way only reflect sampling error and do not take into account the uncertainty as to whether the constraint LORAB= LORAC– LORBC holds for the particular set of trial data. Estimates of uncertainty estimated in this way could be seen as representing the lower bound of uncertainty associated with an indirect comparison.
More Complex Networks
The constraint imposed in an adjusted indirect comparison can be applied to more complex connected networks of trial comparisons in order to obtain consistent estimates of treatment effects. A network is connected if all treatments are connected via direct or indirect comparisons. For example, trials comparing treatments A and B, B and C, and C and D form a connected network whereas trials comparing A and B, and C and D do not.
In a network meta-analysis, estimates of treatment effect are made that comply with the constraint δAB =δAC -δBC on the scale being used for analysis and best fit the observed trial data. These estimates may be obtained using the Bayesian Markov chain Monte Carlo or maximum likelihood methods.
Assumption Of Consistency
The constraint that δAB =δAC-δBC has been referred to as an assumption of consistency (direct and indirect estimates are consistent), exchangeability (e.g., if treatments were exchanged between trials the estimated treatment effects would be the same, allowing for random variation), or transitivity (the relationship δAB= δAC-δBC is transitive, e.g., δAC =δAB + δBC ).
Although it is common to refer to an ‘assumption’ of consistency in an indirect comparison, it is unlikely that it is believed that the relationship δAB = δAC – δBC holds perfectly across a given set of trial data and that direct estimates comparing treatments A and B, if they became available, would conform perfectly (allowing for random variation) to indirect estimates. Rather, the consistency relationship is an approximation that allows us to make useful predictions based on the available data.
Choice Of Scale
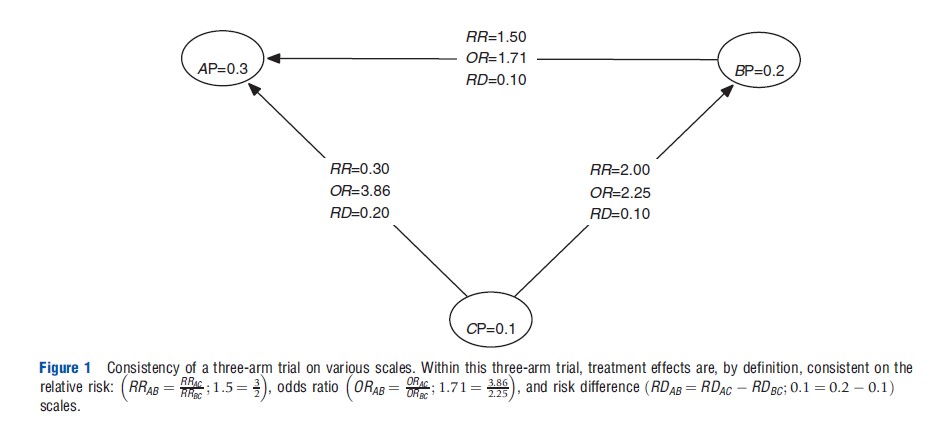
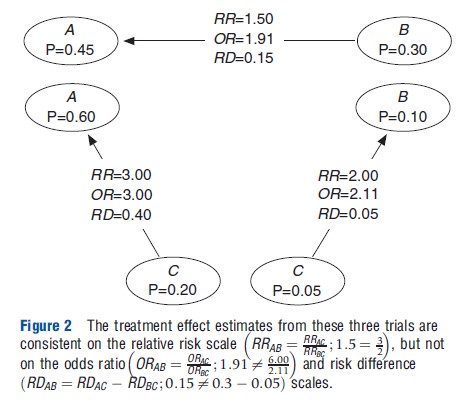
The assumption of consistency can be applied on different scales for the measurement of treatment effect. For example, on the log relative risk (LRR) scale (LRRAB = LRRAC – LRRBC) or the risk difference (RD) scale (RDAB = RDAC – RDBC). These assumptions of consistency are mathematical identities for a single RCT that include treatment A, B, and C (see Figure 1). However, they are not for independent trials comparing A and B, B and C, and A and C. For a set of independent trials, the assumption of consistency may hold on one scale but not another reflect (see Figure 2).
Network Geometry And Testing Consistency
In some networks both direct and indirect estimates of treatment effects may be possible for one or more comparisons. Such a network may be referred to as including loops. The analysis of a network including such loops may be referred to as a mixed treatment comparison (including a mixture of both direct and indirect evidence) and an analysis of a network without such loops as an indirect comparison. The term network meta-analysis is used to refer to any analysis of a connected network of trials evidence including both adjusted indirect comparisons and mixed treatment comparisons.
If the network of trial evidence includes loops it is possible to compare the direct and indirect treatment effect estimates within a network and hence ‘test’ the reliability of the consistency constraint – at least with respect to those comparisons for which direct and indirect evidence is available. The direct and indirect estimates can be compared in using formal hypothesis tests. It should be noted, however, that even where the direct and indirect estimates for a given comparison are consistent, the component treatment effect estimates may not all be exchangeable; the effect of treatment effect modifiers may cancel out across the network.
Figure 1 Consistency of a three-arm trial on various scales. Within this three-arm trial, treatment effects are, by definition, consistent on the relative risk: RRAB =RRAC ; 1.5 =3 odds ratio ORAB /ORAC ; 1.71 = 3.86 and risk difference (RDAB = RDAC – RDBC ; 0.1 = 0.2 – 0.1) scales.
Figure 2 The treatment effect estimates from these three trials are consistent on the relative risk scale but not on the odds ratio and risk difference scales.
Network Meta-Analysis In Practice
Any connected network can be analyzed using the techniques of network meta-analysis. The confidence in the utility of analysis will depend on the empirical evidence regarding the likely deviation of true values of treatment effects from the consistency constraint. If there are material differences between trials in terms of study design (including endpoint definition) or subject characteristics this will reduce the confidence in the analysis.
If there is evidence from subgroup or regression analysis within individual trials that those factors that vary between trials modify treatment effects, this will further reduce confidence in an analysis. Conversely, if these factors do not appear to modify treatment effects within trials this will increase confidence in an analysis.
If there is sufficient overlap in the range of subject characteristics between trials, it may be possible to adjust for the effects of treatment effect modifiers based on an analysis of within-trial variation of response. This may take the form of stratified or regression analysis. Propensity score methods have also been used where individual patient level data analysis is available for some trials and aggregate data for others.
If there are sufficient trials meta-regression analysis of the variation in treatment effects between trials and study characteristics or subject characteristics aggregated at the study level can also be used to adjust for heterogeneity between trials.
If empirical adjustment for heterogeneity between trials is possible, this may increase the confidence in the results in an analysis based on indirect comparisons.
Alternatives
Finally, when considering the utility of a network meta-analysis, it is important to consider the alternatives. Decisions could be based solely on analyses of direct evidence. However, the available direct evidence may be contradictory and difficult to interpret in a piecewise manner. In contrast, a network meta-analysis will provide estimates that are consistent with readily interpretable estimates of uncertainty.
In many cases direct evidence may not be available, in this case the decision could be deferred until direct evidence be- comes available (although when it does it may be inconsistent with the existing indirect evidence); some assumption of equivalent effectiveness might be made; or the response to treatment in individual trial arms compared. The latter is termed a naive indirect comparison.
Whereas a naıve indirect comparison will be confounded by factors that affect the response to treatment in individual trial arms, an adjusted indirect comparison or network meta-analysis based on treatment effect estimates from RCTS analyzed as randomized will only be confounded by factors that act as treatment effect modifiers. Factors that affect response in individual treatments arms, but do not alter the average treatment effect on the scale used for analysis, will not confound network meta-analyses. This has led several commentators to recommend network meta-analysis or adjusted indirect comparisons over naıve indirect comparisons.
It should also be noted that any use of RCT evidence for decision-making infers some form of exchangeability between the subjects within the trial and those patients who are the object of the decision-making process. If multiple trials are viewed as being relevant to the decision-making process for an individual patient, this infers some degree of exchangeability between these trials. Network meta-analysis could be seen as the formalization of this exchangeability.
Conclusions
Network meta-analysis is increasingly used as a framework for estimating the effects of the full range of relevant options. This article has considered the principles of these methods and, in particular, the underlying assumptions needed for reliable estimates.
Bibliography:
- Caldwell, D. M., Ades, A. E. and Higgins, J. P. (2005). Simultaneous comparison of multiple treatments: Combining direct and indirect evidence. British Medical Journal 331(7521), 897–900.
- Caldwell, D. M., Welton, N. J., Dias, S. and Ades, A. E. (2012). Selecting the best scale for measuring treatment effect in a network meta-analysis: A case study in childhood nocturnal enuresis. Research Synthesis Methods 3(2), 126–141.
- Higgins, J. P. T., Jackson, D., Barrett, J. K., et al. (2012). Consistency and inconsistency in network meta-analysis: Concepts and models for multi-arm studies. Research Synthesis Methods 3(2), 98–110.
- Hoaglin, D. C., Hawkins, N., Jansen, J. P., et al. (2011). Conducting indirect treatment-comparison and network-meta-analysis studies: Report of the ISPOR Task Force on indirect treatment comparisons good research practices: Part 2. Value in Health 14(4), 429–437.
- Jansen, J. P., Fleurence, R., Devine, B., et al. (2011). Interpreting indirect treatment comparisons and network meta-analysis for health-care decision making: Report of the ISPOR Task Force on indirect treatment comparisons good research practices: Part 1. Value in Health 14(4), 417–428.
- Jones, B., Roger, J., Lane, P. W., et al. (2011). Statistical approaches for conducting network meta-analysis in drug development. Pharmaceutical Statistics 10(6), 523–531.
- Lu, G. and Ades, A. E. (2004). Combination of direct and indirect evidence in mixed treatment comparisons. Statistics in Medicine 23(20), 3105–3124.
- Lu, G. and Ades, A. E. (2006). Assessing evidence inconsistency in mixed treatment comparisons. Journal of the American Statistical Association 101(474), 447–459.
- National Institute for Health and Care Excellence Technical Support Documents Evidence Synthesis Series. Available at: http://www.nicedsu.org.uk/EvidenceSynthesis-TSD-series(2391675).htm (accessed 28.06.13).
- Salanti, G., Marinho, V. and Higgins, J. P. T. (2009). A case study of multiple- treatments meta-analysis demonstrates that covariates should be considered. Journal of Clinical Epidemiology 62(8), 857–864.
- Signorovitch, J. E. J., Sikirica, V., Erder, M. H., et al. (2012). Matching-adjusted indirect comparisons: A new tool for timely comparative effectiveness research. Value in Health 15(6), 940–947.
- Welton, N. J., Sutton, A. J., Cooper, N. J. and Abrams, K. R. (2012). Evidence synthesis for decision making in healthcare. London: Wiley.