Introduction
In countries such as Australia, the UK, and Canada, public funding decisions for health technologies (e.g., pharmaceuticals) are based predominantly on cost-effectiveness data. National reimbursement bodies in these countries, such as the Pharmaceutical Benefits Advisory Committee in Australia and National Institute for Health and Clinical Excellence in the UK, provide guidance to the government, which form the basis of decisions around public funding of new health technologies. Most often, this process involves using decision analytic models to inform reimbursement approval at the national level.
Decision analytic models are now an expected part of economic evaluations and are used to synthesize data from a variety of sources, link intermediate outcomes to final outcomes (e.g., quality-adjusted life-years), and extrapolate beyond the data observed in a clinical trial.
The process of developing a model requires three key choices to be made regarding (1) model structure (e.g., health states included in the model, transitions between them, and the choice of a modeling technique), (2) analytical methods such as the perspective taken (e.g., government and society) and the discount rate assumed, and (3) model input values (e.g., incidence of disease and costs of treatment). Recommendations to address uncertainty around the choice of analytical methods and model parameterization (values assigned to the model inputs) (i.e., (2) and (3) above) are generally well established and continually refined in the guidelines developed by national reimbursement bodies. Although the impact of uncertainty around the choice of model structure and making incorrect structural assumptions on model outputs, and hence on funding decisions, is acknowledged, relatively little attention has been paid to address these issues in guidelines.
The article focuses on the processes required to specify a model structure and on the uncertainty specifically arising from the choice of a model structure (i.e., structural uncertainty). The specification of a model structure involves the choice of health states or events to include in the model, and the relationships to be represented between those states.
There are a range of issues to be addressed; firstly defining an appropriate model structure, and subsequent considerations around the feasibility or applicability of the appropriate structure. Key issues include the transparency of the model to end users and the potential effects of model complexity on the process of establishing the internal and external validity of the model. In some cases, model structure may be amended on the basis of the time available to implement, validate, and analyze a model, and/or the data available to populate a model.
Another key part in the development of a model is the choice of modeling techniques, which provide an implementation framework that is used to implement a defined model structure. Inappropriate choice of modeling techniques may influence the outputs of a decision analytic model, and hence needs to be taken into account.
Decision trees are not generally applicable to the process of extrapolation, and so the major area of choice for models that estimate long-term costs and benefits is around the use of cohort-based models (predominantly cohort state-transition models), and individual-based models (generally, either statetransition models or discrete event simulation (DES)). Individual sampling models allow attributes to be assigned to patients that reflect baseline characteristics of patients and/or events experienced within the model. Such characteristics can only be represented in a cohort model by increasing the number of health states included in the model structure. Individual-based models require more analysis time as individuals rather than cohorts are run through the model.
The preceding elements of model-based studies represent the structural features of a decision analytic model. Although concerns have been raised regarding assumptions incorporated into model structures, there is a lack of clarity around the choice of model structure.
The article unfolds as follows: The first section outlines issues around the choice of an appropriate conceptual framework. This framework should reflect the natural history of the condition under study, and defines the states/events to be represented, the relationships between them and the effect of patient characteristics on the probability and timing of events. The second section discusses the development of an appropriate modeling technique (i.e., the choice of an appropriate implementation framework). The third section briefly provides a guide to the terminology used in defining different types of uncertainty around decision analytic models with a focus on structural uncertainty. Then the methods that can be used to deal with structural uncertainty are explored. The concept of reference models and their potential benefits are discussed in section five. Thereafter, the authors illustrate the application of the proposed framework for defining an appropriate model structure, taking major depressive disorder as a case study. Conclusions are formed in the final section.
Choice Of An Appropriate Model Structure: Conceptual Framework
All valid models are based on an appropriate conceptual framework. The specification of an appropriate conceptual framework involves two key features, that is, the structural assumptions that inform the choice of health states/events to include in the model, and the relationships to be represented between those states (i.e., transitions between clinical events). The International Society for Pharmacoeconomics and Outcomes Research – The Society for Medical Decision Making Joint Modeling Good Research Practices Task Force reports on the conceptualization of a model provides guidance for the development of an appropriate model structure.
A realistic model structure should comprise key clinically relevant events relating to the natural history of the condition being evaluated. To develop an appropriate conceptual framework, a thorough review of the clinical literature related to the condition under study should be undertaken. This review will document the progression of the condition and summarize a set of main clinical events and their interrelationships, as well as relevant patient’s attributes that influence disease pathways and/or response to treatment. A review of the existing models should also be undertaken to inform the importance of identified states/events from the economic perspective. The clinical events identified will be disaggregated where there are likely to be important differences between events with respect to expected disease progression, associated costs, or associated outcomes (e.g., quality of life). If the current evidence is conflicting, more than one plausible model framework can be proposed.
There are additional issues to consider during the specification of a model structure. The choice of model structure should balance the potential value of additional model complexity, that is, increasing the likelihood of identifying important differences in the costs and benefits of the alternative health care interventions being compared, against the potential for reduced transparency, and ease of implementation, which may affect internal validity (i.e., the likelihood of undetected errors in the model). Another issue to consider is the availability of data to populate and externally validate the model (e.g., the extent to which predicted model outputs replicate the observed data, or correspond with outputs from other models in the same area). These issues are related, and all concern the credibility of model outputs.
Transparency And Validity Of The Framework
Transparency refers to the ability of the end user (or a delegate of the end user, i.e., an independent reviewer) to understand and assess the implemented model. Where a specific end user is identified, the importance of this issue should be established in consultation with the end user.
The importance of model transparency may be ameliorated if the analyst can clearly demonstrate the face validity of the model. This may take the form of an expert review of the implemented model by an analyst who was not directly involved in the implementation of the model, or who was independent of the entire evaluation. Inputs from experts will be sought as to whether the proposed model structure(s) sufficiently reflects the relevant disease process and disease management pathways. Alternatively, a set of analytic checks may be defined that demonstrate the internal accuracy of the model, for example, using extreme parameter values. In defining the final model structure, the analyst should consider the extent to which they will be able to meet transparency criteria and/or demonstrate the validity of the model.
More complex model structures generally require the estimation of a greater number of input parameters, which may preclude the estimation of particular parameter values or require the use of less reliable data sources, such as data elicited from experts. Alternatively, more complex models may provide greater flexibility with respect to identifying targets for calibration or external validation.
Data Sources For Model Population
A systematic review of the literature and a thorough investigation of relevant data sources (e.g., published literature, national registries, or patient-level database) should be undertaken to identify all potentially useful sources of data, to which appropriate analytic methods can be applied to populate and validate the model. However, if this fails to identify relevant and sufficiently valid data to inform the estimation of all the required input parameters to construct the model, an expert elicitation process can be undertaken to explore the possibility of using expert opinion to fill gaps in data.
It should not be assumed that all missing parameters can be elicited from experts, as there is evidence that experts are sometimes unable or unwilling to estimate parameters about which they are too uncertain.
Expert elicitation is subject to a range of biases; both intentional and unintentional (e.g., recall bias). Before a decision is made to use elicited parameter values, and thus maintain the preferred model structure, values elicited from experts should be validated by asking additional questions in which elicited parameter values can be compared with empirical data. Elicited parameter values can also be crosschecked, that is, comparing expert data from independent sources. It is also important to represent the certainty with which different parameters can be estimated by experts, for which established methods can be applied that also provide transparency.
Missing parameter values may also be estimated using calibration techniques, by identifying sets of input parameter values that produce model outputs that are similar to target values (i.e., observed estimates of the output parameters). Calibration is a useful process even when empirical estimates for all input parameters are available, especially for complex models with many uncertain parameters.
If specific input parameters cannot be directly estimated, and relevant calibration targets cannot be identified (i.e., targets that are part-determined by parameters for which direct data is absent), potential modifications to the model structure should be considered. Decisions around data-related structural modifications should be informed by the importance of the parameters that would be omitted from a modified model structure.
Ideally, the importance of parameters with missing values would be established by implementing and populating the originally specified model structure and testing the sensitivity of the model’s outputs to extreme values for the missing parameters. The paradox of this process is that the more complex model is likely to be used regardless of the outcome of this testing process – if the model is not sensitive to these parameters then a less complex model would suffice, but the analyst has already built the more complex model.
Time Constraints
In some cases, it may also be necessary to consider the timelines for the economic evaluation. If a model is being developed to inform a national reimbursement body, which has requested results from the evaluation in a time period that precludes adequate processes for the population, validation, and analysis of a preferred model structure, it may be advisable to reduce the complexity of an ideal model structure.
In all cases where a preferred model structure is modified on the basis of any of the above considerations, the process and rationale for making such decisions should be documented and reported. Here, the ‘art of modeling’ may be used, whereby the modeling team use their combined clinical and analytical experience to consider and report the potential effects of any structural modifications on the estimated costs and benefits, and in particular on the differences in cost and benefits between competing interventions.
Choice Of An Appropriate Modeling Technique: Implementation Framework
There are various modeling techniques that can be used for the economic evaluation of health care interventions. Full details of different types of modeling techniques are beyond the scope of this article and need not be rehearsed here. In this section, the authors briefly present the key features of the three techniques commonly being used in the literature, that is, decision trees, cohort state-transition models, and individual-based models.
Decision Trees
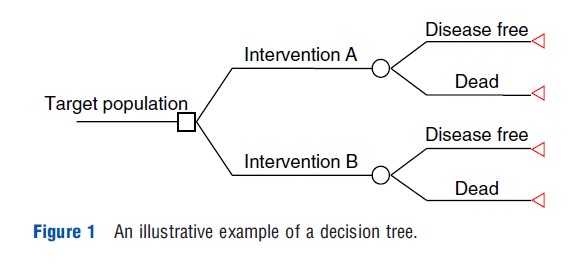
Decision trees (DTs) are the simplest modeling techniques and are most appropriate for modeling interventions in which the relevant events occur over a short time period. The main limitation of decision trees is their inflexibility to model decision problems, which involve recurring events and are ongoing over time. In general, DTs are constructed with three types of nodes, namely decision nodes, chance nodes, and terminal nodes. A simple illustrative decision tree is presented in Figure 1. The tree flows from left to right starting with a decision node (square) representing the initial policy decision (alternative interventions in Figure 1). Each management strategy is then followed by chance nodes (circles) representing uncertain events (i.e., ‘disease free’ or ‘dead’ in Figure 1), which will have probabilities attached to them. Finally, endpoints of DTs are represented by a terminal node (triangle) at the right of the tree. The outcome measures (e.g., utility value) are generally attached to these endpoints. Costs, however, are attached to events within the tree, as well as to endpoints. The expected values (costs and effectiveness) associated with each branch are estimated by ‘averaging out’ and ‘folding back’ the tree from right to left.
Cohort State-Transition Models
Cohort state-transition models (CSTM) are the standard technique used to model the economic impact of health care interventions over time. Using these models to capture long-term costs and benefits (e.g., lifetime), disease progression is conceptualized in terms of a discrete set of health ‘states’ and the ‘transitions’ between them. In health technology assessment, most state-transition models are discrete-time models in which the time horizon of the analysis is split into cycles of equal length (Markov cycles).
A CSTM assumes a homogenous population cohort moving between states (or staying in the same state) in any given cycle. Transitions between states during cycles are based on a set of conditional probabilities (i.e., transition probabilities). These probabilities are conditional upon the current health state. The movement between discrete health states (such as depressive episodes or remission) continues until patients enter an absorbing state (e.g., ‘death’) or up to the end of the specified time horizon. Costs and outcome (e.g., utility weights representing quality of life) are attached to each health state (i.e., state rewards) and transitions (i.e., transition rewards if appropriate) in the model. Expected costs and quality-adjusted life-years (QALYs) are estimated over the time horizon of the model as the sum of the time spent in each health state multiplied by the respective cost and utility weights for each health state.
CSTMs, however, suffer from the lack of memory (i.e., Markovian assumption) in which transition probabilities are not influenced by pathways taken to a particular health state. By creating separate states in a Markov model, it is technically possible to address the above issues. However, this can result in an unwieldy number of events/states and may make model implementation, checking, and analysis difficult.
Individual-Based Models
Individual-Based State-Transition Models
These models are able to carry histories whilst remaining a manageable size. These models include all the key features of the cohort Markov family. However, assigning relevant attributes to individuals rather than to health states within a model means that the effect of the Markovian assumption is removed. They transit individual patients through the model rather than proportions of a cohort. If and where the patient moves during cycles is determined by random numbers drawn from a uniform distribution. A large number of patients are run through the model and the mean costs and QALYs gained across all patients are estimated. The principal advantage of these models is that patients’ treatment and/or disease history can be captured, and used to inform subsequent transition probabilities applied to each patient within the model.
A limitation of individual-based state-transition models, however, is that time is managed through a fixed cycle length (e.g., monthly) by which the model moves forward. This may not reflect accurately the length of time spent in certain states as patients can only experience one event within each cycle. It is possible to address this issue by selecting shorter cycles (i.e., weekly) or linking separate models each with different cycle lengths. However, it may be easier to use a more flexible individual-based technique, i.e., discrete event simulation (DES).
Discrete Event Simulation
DES is a very flexible model that describes the flow of individuals through the treatment system. In DES, patients can be assigned attributes such as age, gender, or disease history which are assumed to influence patient’s pathways through the model.
DES can accommodate differing cycle lengths more easily and with greater accuracy than state-transition models. DES uses a stochastic process to simulate events for an individual by sampling probabilities from survival distributions. Times (to next possible events) are sampled and the earliest time represents the next event for a particular individual. These events are added to a calendar and probability distributions are updated conditionally on patient history. This means that the time spent in a particular state can be estimated exactly.
Uncertainty In Decision Analytic Models: Structural Uncertainty
Given the lack of complete information about the key aspects of a decision analytic model (e.g., choice of the health states/ events or true values of costs and effects of a particular intervention in a given population), uncertainty is inherent within any model-based evaluation. Uncertainty (or sensitivity) analysis is necessary so that policy-makers can incorporate information on the accuracy of model outputs into decisions around funding of the competing interventions being evaluated, as well as decisions regarding the need for additional information.
To illustrate different types of uncertainty associated with decision analytic models, the authors present a simple statetransition depression model (Figure 2). The model presented in Figure 2 consists of three states: ‘well,’ ‘depression,’ and ‘dead.’ The aim is to estimate differences in the time spent in each state by patients receiving alternative technologies, over a defined time horizon (e.g., patients’ lifetime). Costs and outcomes are then attached to the time spent in each state to estimate the costs and benefits of alternative technologies.
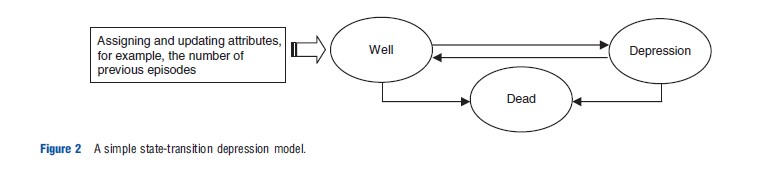
In state-transition models, time progresses in equal increments (e.g., monthly) known as cycles. The arrows represent possible transitions between states, for which transition probabilities are estimated. Relevant attributes (which influence disease pathways or response to treatment) can be assigned to patients, and updated during the course of running the model. For example, the probability of recurrence (i.e.,‘well’ to ‘depression’) increases with the number of previous depressive episodes that patients experienced.
Three broad forms of uncertainty have been distinguished: parameter, methodological, and structural. Parameter uncertainty concerns the uncertainty around the true value of a given parameter within the model (e.g., probabilities of moving between ‘well’ to ‘depression’). Methodological uncertainty relates to the choice of analytic methods such as the perspective taken (e.g., society and government) with an impact on, for example, the process of identifying resource items. Issues around parameter and methodological uncertainties are generally dealt with, for example, by using probabilistic sensitivity analysis and by prescribing a ‘reference case,’ respectively. Structural uncertainty arises from the assumptions imposed by the modeling framework and refers to the structural features of the chosen model, that is, the choice of clinical events represented in a model (e.g., adding a ‘partial response’ state to the model presented in Figure 2), and the possible transitions between them.
It is recognized that the choice of model structure can lead to different results, hence different reimbursement decisions. Although concerns have been raised regarding assumptions incorporated into model structures, and that structural uncertainty may have a greater impact on the model’s results than other sources of uncertainty, relatively little attention has been paid to the representation of structural uncertainty. Different ways to address structural uncertainty are discussed in Section ‘Uncertainty in Decision Analytic Model.’
Addressing Structural Uncertainty
Like uncertainty around methodological issues and the value of input parameters, structural uncertainty cannot be eliminated, and needs to be handled appropriately. Different approaches are used to characterize structural uncertainty.
The simplest approach to representing structural uncertainty is to implement and analyze a range of alternative model structures, and to present the results from each model as scenario analyzes. However, this approach puts the burden of assessing the relative credibility of the alternative structures on the end user, which may result in only a superficial and subjective assessment that will not reflect the full value to the decision-making process of implementing multiple model structures.
For the characterization of structural uncertainty, two techniques have been identified: model selection and model averaging. Both techniques involve developing a set of plausible models using different structural assumptions.
The ‘model selection’ approach ranks alternative models according to some measure of prediction performance or goodness of fit, and selecting the single model that maximizes that particular criterion. This approach does not represent structural uncertainty, rather it identifies the model that is believed to be the most likely to be the correct model. The effect of selecting a single model will depend on the relevance of the criterion used to select the model and the magnitude of the difference in the predictive power of the alternative model structures. Moreover, given the effort required to build and analyze a range of alternative model structures, it would appear wasteful to report results based only on a single model when there is a likelihood that the other models could be a more correct model.
‘Model averaging’ methods assess structural uncertainty by assigning weights to a range of alternative model structures according to some measure of model adequacy. Weighted model outputs are then estimated across all model structures included in the model averaging process. The weightings should reflect the probability that each model is the correct model, based on some measure of predictive power (e.g., Akaike’s information criterion). The main limitation of the quantitative approach to model averaging is the necessary restriction of the process to represent the elements of structural uncertainty that are linked to outputs for which observed data are available.
Other model averaging applications have elicited weights to be applied to each of the defined model structures. Here, the analyst must consider the potential for biased responses and superficial assessment of the relative merits of the alternative models.
Alternatively, a discrepancy approach has been applied to represent the uncertainty around an implemented model structure. Unlike model averaging, the discrepancy approach does not assess the adequacy of the model structure in relation to alternative structures. Rather, the joint effects of structural and parameter uncertainty are estimated, i.e., the estimated distribution of the costs and benefits of the competing interventions reflects structural and parameter uncertainty.
The application of the discrepancy approach requires the identification of points of discrepancy (i.e., structural uncertainty) within a model structure, and the subjective estimation of the magnitude and variance of the discrepancy between predicted outputs from the model using true values for each input parameter and the true values of the predicted parameters.
Improving The Accuracy And Consistency Of Model-based Evaluations: The Case For Reference Models
One of the main consequences of structural uncertainty is that alternative economic evaluations for a specific disease use alternative model structures (e.g., alternative model structures to evaluate different pharmaceuticals for treating depression). In addition to the structural uncertainties around each model structure, indirect comparisons of the cost-effectiveness of these interventions are further hindered by the diversity in model structure. Using different model structures in evaluations of alternative technologies for the same condition in submissions to national reimbursement bodies can lead to inconsistent public funding decisions because changes in model structure and analysis can produce substantially different results. This increases the likelihood of incorrectly identifying a new technology as being cost-effective (and vice versa).
There is potential for strategic behavior when defining a model structure, by focusing on aspects of the disease process that are targeted by particular technologies, for example, if drug A reduces risk of event X but not event Y and event Y has significant costs and/or quality of life effects, if the model structure represents only X then important aspects of the disease are not included and the results are biased.
To address these concerns, there is a need for a detailed and transparent framework for developing an appropriate common model structure (reference models) for specific diseases (e.g., depression, colorectal cancer, etc.) for economic evaluations to inform public funding decisions. The structure of a reference model defines the clinical events to be represented, the relationships between the events, and the effect of patient characteristics on the probability and timing of events. The model should accurately represent both the knowledge and uncertainty about states/events relating to the disease progression on the basis of the best available evidence. Reference models can be applied to a wide set of interventions for a specific disease (e.g., drugs and procedures that may target alternative mechanisms or stages of disease). For example, a reference model for depression could be used to estimate the costs and benefits of competing antidepressants, as well as evaluating the costs and benefits of alternative models of care (e.g., usual care vs. enhanced care).
By reflecting the natural history of the condition under study more accurately, reference models can improve the accuracy, comparability, and transparency of public funding decisions for new health technologies. However, we emphasize that reference models are not intended to replace structural sensitivity analyzes, and approaches to address structural uncertainty might be still required if there is insufficient evidence (or conflicting evidence) to support an appropriate model structure.
A national reimbursement body could commission the development of reference models for key disease areas, which are then developed according to best practice (as outlined in the preceding sections). The resulting models could be subjected to a thorough process of structural uncertainty analysis, and would ultimately provide a comprehensive and unbiased representation of the disease, including all important clinical and economic aspects (e.g., costs and quality of life effects), which may affect the long-term estimation of costs and benefits of the alternative health care interventions being compared. In terms of the feasibility of using reference models, one of the possibilities will be, for example, to provide the reference model to any industry applicant intending to submit a technology in the relevant disease area by national reimbursement bodies. Applicants could update the inputs used to populate the model, but would be expected to revalidate the model. Likewise, applicants would be free to use an alternative model structure, but it would have to be fully justified. The outputs of alternative models can be compared against the reference model, which provides a basis for confirming any claimed advantages of new model structures.
Case Study: Major Depressive Disorder
After reviewing the course of depression, this section discusses the issues surrounding structural assumptions used to inform a preferred model structure and the choice of modeling techniques, using examples from published model-based economic evolutions of interventions from the treatment of depression.
Background To The Course Of Depression
Major depressive disorder (referred to as depression henceforth) is the most common mental health disorder. Depression is associated with a considerable functional impairment, morbidity, and premature mortality. It is increasingly recognized as a chronic disease characterized by multiple acute episodes/ relapses.
A common set of terminology describing different stages of disease progression has been proposed. ‘Response’ represents a significant reduction (50% or more reduction from baseline scale scores) in depressive symptoms. ‘Remission’ represents a period during which the patient is either symptom free or has no more than minimal symptoms. ‘Recovery’ is defined as an extended asymptomatic phase, which lasts for more than 6 months. ‘Relapse’ is a flare up of the depressive episode, which occurs after remission, whereas recurrence is a new depressive episode that occurs after recovery.
Chronic depression is one of the clinically meaningful structural aspects of depression and is defined as a persistent depressive episode, which is continuously present for at least 2 years, or an incomplete remission between episodes with a total duration of illness of at least 2 years. High-risk patients and those who have not responded adequately to outpatient treatment can be admitted to hospitals. Finally, all patients can die, with an increased risk of death due to suicide while in a depressive episode.
Patients with depression may be treated with different classes of antidepressant drugs, including selective serotonin reuptake inhibitors and serotonin norepinephrine reuptake inhibitors. After a successful short-term treatment, antidepressants need to be continued for a period to prevent relapse (continuation therapy) and to prevent recurrence (maintenance therapy). Psychotherapy or more commonly a combination of pharmacotherapy and psychotherapy are other options in treating patients with depression.
Choice Of An Appropriate Conceptual Framework
The choice of health states/events included in the model is considered as a key part in developing decision analytic models. An appropriate model structure should reflect a number of key clinically relevant health states relating to the course of the disease under study. Over recent years, various model structures were used in depression studies.
Some model-based studies of depression included only response as a primary outcome measure in their model. This model structure is not appropriate as it is likely to bias results in favor of treatments with higher rates of response, which may be the more or less effective treatment overall.
In some studies, the possibility of relapse (i.e., remission to depressive episodes) and/or recurrence (i.e., recovery to depressive episodes) was not considered. By excluding these clinical events, studies implicitly assume that the incidence of such is unlikely to differ between competing management strategies. As a recurring illness, this simplification in the model structure in depression studies will favor treatments with higher remission rates. A more appropriate model structure is to represent both levels of treatment success (i.e., response and remission) and treatment failure (i.e., relapse and recurrence).
Hospital admission for high-risk patients or those who have not responded adequately to outpatient treatment is another relevant clinical event. A realistic model of depression should represent this event as it represents clinical practice more accurately.
‘Chronic depression’ is another relevant event that is important from both clinical and economic perspectives. Approximately 20% of patients with acute episodic illness will develop a chronic course of depression. It has been noted that chronic depression, compared with nonchronic depression, is associated with increased health care utilization, more suicide attempts, and greater functional impairment requiring a longer duration of treatment.
Finally, given a baseline increased risk of suicide at rates 10–20 times above general population rates, the omission of such a state from a depression model will likely bias the model in favor of less effective interventions.
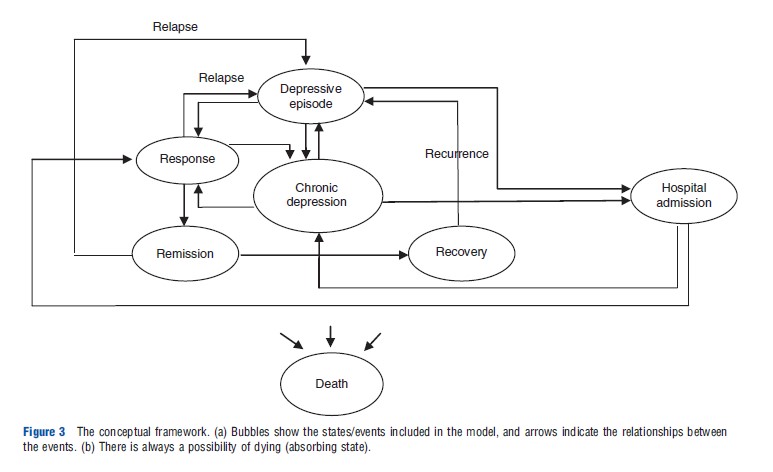
Accepting the above course of disease, the model structure and relationships between events are presented in Figure 3. In this model, depressive episodes represent relapse or recurrence.
Choice Of An Appropriate Computational Framework
Some studies of depression used DTs to evaluate costs and effects of alternative management strategies. Given that depression is a chronic illness with recurrent episodes, the main limitation of DTs is their inflexibility to model long-term events. The likely impact of the choice of a DT with a short time horizon on the cost-effectiveness results, and hence policy decisions, will vary according to the short-term cost-effectiveness results. If a more effective treatment (i.e., fewer deaths and/or more remission) can demonstrate cost-effectiveness within a short time horizon, it may be reasonable to expect that this result would not change over an extended time horizon. The likely magnitude of potentially underestimated cost differences should be considered, but a DT may be appropriate in this scenario. Where the more effective treatment is not shown to be cost-effective using a DT, it may be possible to imply the likely cost-effectiveness over a longer time horizon, though a modeled extrapolation provides a more explicit and transparent process of estimation.
By including recurring events and breaking up a decision tree to sequential time periods, it is technically possible to capture recurring events over longer time periods. This, however, progressively increases the size of the model and the use of an alternative modeling technique might be preferred.
To address the above issue, some model-based studies of depression employed CSTMs. These models allow for an evaluation of recurring events over a longer period of time, for example, multiple depressive and recovery episodes. However, the lack of memory (i.e., Markovian assumption) is considered as a major limitation of these models. In the case of depression, the above assumption means that an individual in the ‘full remission’ state with only one previous depressive episode has the same probability of experiencing ‘recurrence’ as a patient with a history of multiple depressive episodes. This, however, does not appropriately represent the natural history of depression as the risk of recurrence has been found to increase with the number of previous depressive episodes. One way to overcome this limitation is to create separate states to represent differing numbers of previous depressive episodes, for example, ‘remission, one previous episode,’ ‘remission, two previous episodes,’ etc. As implied, this process can soon result in an unwieldy number of health states, and may make model implementation, checking, and analysis difficult.
By modeling individual patient pathways, individual-based state-transition models are able to carry patient histories whilst remaining a manageable size.
Assigning attributes such as the severity of episodes to individuals rather than to health states within a model means that the effect of the Markovian assumption is removed. Individual-based models then facilitate the estimation of probability and timing of experiencing relevant events as a function of patient-recorded attributes (e.g., age, gender, severity, comorbidity, and psychotherapy as attributes). By updating attributes, probabilities can change over time while the model is running.
One practical limitation associated with the use of individual-based state-transition models is the need to define a fixed cycle length by which the model moves forward in time. The cycle length should represent a clinically relevant time span. Modeling studies of depression that use a fixed monthly cycle length may not reflect accurately the length of time spent in certain states as patients can only experience one event within each cycle. It is possible to address this limitation by selecting shorter cycles (i.e., weekly) or linking separate models each with different cycle lengths. However, it may be easier to use a more flexible modeling technique, that is, DES. No model-based studies of depression using DES were located.
DES can accommodate differing cycle lengths more easily and with greater accuracy than state-transition models. In a DES, time does not move forward in cycles, but rather with respect to the sampled timing of events, for example, if a patient relapses after 2 weeks, the model moves forward from time zero (treatment initiation) to time 14 days. If the next event (e.g., remission) occurs 2 months later, then the DES would move forward directly to that time point. Using survival distributions, times (to next possible events) are sampled, and the earliest time represents the next event for a particular individual. This means that the time spent in a particular state can be estimated exactly.
Considering disease characteristics, the authors argue that DES is the appropriate modeling technique for depression studies to project life-time benefits and resource costs of management options in patients with depression.
Data Sources
A variety of data sources are used to derive clinical parameters.
Clinical Trials And Observational Studies
Using data derived from clinical trials or observational studies, it is widely accepted that ‘response’ is defined as at least a 50% improvement in baseline scores recorded by the most cited assessment tools, i.e., the Hamilton Depression Rating Scale (HAM-D). HAM-D is considered as the gold standard to measure the severity of depression and is used in the majority of clinical trials of depression. ‘Remission’ is mostly defined as a score of 7 or less on the 17-item HAM-D. The occurrence of ‘depressive episodes’ is commonly defined when patients meet the criteria identified by DSM IV.
Retrospective Databases
Clinical outcome measures using standard assessment tools are not typically recorded in data sources such as claims databases and medical notes. Thus, proxy measures such as treatment changes should be defined. For example, relapse can be defined as a subsequent antidepressant prescription less than 6 months after the antidepressant stop date. Another form of observational data is claims databases (e.g., US managed care database).
Expert Opinion
Expert opinion is another source of data, which was used in a few studies to estimate probabilities of clinical inputs such as dropout rates, reasons for discontinuation, and nondrugspecific events such as relapse rate after discontinuation. An elicitation method is intended to link an expert’s underlying opinions to an expression of these in a statistical form, and is an appropriate technique to fill gaps in data where no published information is available. However, it is important to have transparent criteria for the selection of participants, and to recognize the potential for biased estimates that may be in favor of the participant personal experiences (e.g., more frequent patients with the most severe symptoms) and/or preferences.
Conclusions
To date, relatively little attention has been paid to the processes and issues around the specification of appropriate decision analytic model structures, but better specified decision analytic models will contribute to more consistent and better informed decisions for the allocation of limited resources.
This article has addressed issues around the appropriate choice of model structure for the purposes of economic evaluations of health care technologies, including discussions around the choice of appropriate modeling technique, representation of structural uncertainty, and the potential benefits of the development of disease-specific reference models. The disease area of depression was used to illustrate the issues involved in the process of specifying an appropriate model structure.
References:
- Barton, P., Bryan, S. and Robinson, S. (2004). Modelling in the economic evaluation of health care: Selecting the appropriate approach. Journal of Health Services Research and Policy 9, 110–118.
- Bojke, L., Claxton, K., Sculpher, M., et al. (2009). Characterizing structural uncertainty in decision analytic models: A review and application of methods. Value in Health 12, 739–749.
- Brennan, A., Chick, S. and Davies, R. (2006). A taxonomy of model structures for economic evaluation of health technologies. Health Economics 15, 1295–1310.
- Briggs, A. H., Weinstein, M. C., Fenwick, E. A., et al. (2012). Model parameter estimation and uncertainty analysis: A report of the ISPOR-SMDM Modelling Good Research Practices Task Force-6. Medical Decision Making 32, 722–732.
- Brisson, M. and Edmunds, W. J. (2006). Impact of model, methodological, and parameter uncertainty in the economic analysis of vaccination programs. Medical Decision Making 26, 434–446.
- Eddy, D. M., Hollingworth, W., Caro, J. J., et al. (2012). Model transparency and validation: A report of the ISPOR-SMDM Modelling Good Research Practices Task Force–7. Medical Decision Making 32, 733–743.
- Haji Ali Afzali, H. and Karnon, J. (2011). Addressing the challenge for well informed and consistent reimbursement decisions: The case for reference models. Pharmacoeconomics 29, 823–825.
- Haji Ali Afzali, H., Karnon, J. and Gray, J. (2012). A critical review of model-based economic studies of depression: Modelling techniques, model structure and data sources. Pharmacoeconomics 30, 461–482.
- Jackson, C., Sharples, L. D. and Thompson, S. G. (2010). Structural and parameter uncertainty in Bayesian cost-effectiveness models. Applied Statistics 59, 233–253.
- Karnon, J. and Brown, J. (1998). Selecting a decision model for economic evaluation: A case study and review. Health Care Management Science 1, 133–140.
- Le Lay, A., Despiegel, N., Francois, C., et al. (2006). Can discrete event simulation be of use in modelling major depression? Cost effectiveness and resource allocation 4, 19.
- Roberts, M., Russell, L. B., Paltiel, D., et al. (2012). Conceptualizing a model: A report of the ISPOR-SMDM Modelling Good Research Practices Task Force-2. Value in Health 15, 804–811.
- Russell, L. B. (2005). Comparing model structures in cost-effectiveness analysis. Medical Decision Making 25, 485–486.