Introduction
The goal of an economic evaluation of medical interventions is to provide actionable information for policy makers. Modern policy decision makers are driven by data-backed arguments regarding what might change as a result of an intervention. As analysts, this requires specific attention to determining the causal impact between a given intervention and future outcomes. To justify a change in the way medicine is practiced, correlation is not sufficient; detecting and quantifying causal connections is necessary.
Medicine has relied on randomized controlled studies as the gold standard for detecting and quantifying causal connections between an intervention and future outcomes. Randomization offers a clear mechanism for limiting the number of alternate possible explanations for what generates the differences between the treated and control groups. The demand for causal evidence in medicine far exceeds the ability to practically control, finance, and/or conduct randomized studies. Observational data offer a sensible alternative source of data for developing evidence about the implications of different medical interventions. However, for studies using observational data to be considered as a reliable source for evidence of causal effects, great care is needed to design studies in a way that limits the number of alternative explanations for observed differences in outcomes between intervention and control. This article highlights a number of the techniques and tools used in high-quality observational studies. A few of the common pitfalls to be aware of are also discussed.
Example
The development of medical care for premature infants (preemies) has been a spectacular success for modern medicine. This care is offered within neonatal intensive care units (NICUs) of varying intensity of care. Higher intensity NICUs (those classified as various grades of level 3 by the American Academy of Pediatrics) have more sophisticated medical machinery and highly skilled doctors who specialize in the treatment of tiny preemies.
Although establishing value requires addressing questions of both costs and outcomes, the example will focus on estimating the difference in rates of death between the higher-level NICUs and the lower-level NICUs. Using data from Pennsylvania from the years 1995–2005, the authors start with a simple comparison of the 1.25% rate of death at low-level facilities to the 2.26% rate of death at high-level facilities. This higher death rate at high-level facilities is surprising only if one assumes preemies were randomly assigned to either a high or low-level NICU, regardless of how sick they were. In fact, as in most health applications, the sickest patients were routed to the highest level of intensity. As a result, one cannot necessarily attribute the variation in the outcome to variation in the treatment intensity. Fortunately, the data provide a detailed assessment of baseline severity with 45 covariates including variables such as gestational age, birth weight, congenital disorder indicators, parity, and information about the mother’s socioeconomic status. Yet even with this level of detail, the data cannot characterize the full set of clinical factors that a physician or family considers when deciding whether to route a preemie to a high-intensity care unit. As can be seen, these missing attributes will cause considerable problems later on.
What is wanted is not the naıve comparison of rates of death – that is the percentage of preemies who died at the different types of NICUs – but one would like to have the difference in probabilities of death for each preemie given whether the preemie was to be delivered at a low-level facility or a high-level facility. This will be called the causal effect of treatment. This concept is formalized in Section Parameters of Interest.
The Fundamentals
The Potential Outcome Framework
The literature has made great use of the potential outcomes framework (as described in Neyman, 1990; Rubin, 1974; Holland, 1986) as a systematic, mathematical description of the cause-and-effect relationship between variables. Suppose for the moment, assume there are three variables of interest: the outcome of interest Y, the treatment variable T, and X as a vector of covariates. For most of this article, it will be assumed that there are only two treatment levels (e.g., the new intervention under consideration vs. the old intervention), though this assumption is only for simplicity’s sake and treatments with more than two levels are permissible. These two levels shall be referred to using the generic terms ‘treatment’ and ‘control,’ without much discussion of what those two words mean aside from saying that they serve as contrasting interventions to one another. In the potential outcomes framework, the notion is that each individual has two possible outcomes – one which is observed if the person were to take the treatment and one if the person were to take the control. In practice one is only able to observe one of these outcomes because taking the treatment often precludes taking the control and vice versa. The notation used for subject i taking the treatment is Ti= 1 and for patient i taking the control is Ti = 0. To formally denote the outcome subject i would experience under the treatment and control the authors write Y(Ti =1) and Y(Ti=0), respectively. Informally the notation is simplified to Yi(1) and Yi(0) for the potential outcome under treatment and the potential outcome under control. This article will think of Y being a scalar, though it is possible to develop a framework where Y is a vector of outcomes.
Excellent resources exist for reading up on the potential outcomes framework: Rosenbaum (2002), Pearl (2009), and Hernan and Robins (2013).
Now there is enough mathematical language to describe the ultimate, often unattainable, quantity of interest – namely, ‘the individual level treatment effect:’
![]()
Thus ∆i will tell us the difference in outcome, for subject i, between taking the treatment and control. If one could observe this quantity then the benefit from intervention would be known explicitly. But, in practice only one is observed or the other of the potential outcomes. To see this, one may write the observed outcome, denoted Yiobs for the ith individual, as a function of the potential outcomes (Neyman, 1990; Rubin, 1974):
![]()
Observing one of the potential outcomes precludes observing the other. In all but the most contrived settings, this problem is intractable. One will not be able to observe both the treatment and control outcomes. So one must turn to other parameters of interest.
Parameters Of Interest
Suppose we, as the analysts, have collected characteristics of the subjects in our study. It is important to stress that these baseline characteristics should be based on the state of the subject before the intervention to avoid the potential to bias the treatment effect (see Cox, 1958, section 4.2 and Rosenbaum, 2002, pp. 73–74). For example, say a new drug is being tested for its ability to lower the risk of heart attack. High blood pressure is known to correlate with higher risk of heart attack, so it is tempting to control for this covariate. Controlling for blood pressure is likely to improve the precision of the estimate if a pretreatment blood pressure measure is used. It would be a mistake to use a post-treatment measurement of blood pressure as a control because this measurement may be affected by the drug and would thus result in an attenuated estimated causal effect. Intuitively, this is because the estimation procedure is limiting comparison in outcome not just between people who took the drug and who didn’t but between people who took the drug and then had a certain level of blood pressure to people didn’t take the drug and had the same level of blood pressure. The impact from the drug may have already happened via the lowering of the blood pressure.
Let us denote these measured pretreatment characteristics as Xi for the ith subject. Furthermore, the subjects are likely to have characteristics which were not recorded. Let us denote these unobserved characteristics as Ui for the ith subject. There is a not unreasonable belief that the observable outcomes can be thought of as a function of these covariates (in this notation you can think of the treatment level as being an observed covariate). That is Yiobs=f(Xi,Ui). To keep things simple it will be assumed that the covariates are linearly related to the outcomes like so
![]()
![]()
Note that one needs to index the coefficients by the treatment level in order to account for interactions between the treatment level and the covariates. Also, it may appear strange putting coefficients on the unobserved variables, but this is required at the bare minimum to make the dimensions agree. In practice one gets a bit sloppy and write εi(T) in place of the clunkier Uia(T), but this is a move of convenience rather than discipline. It is known that there is not just one scalar, unobservable covariate that has been omitted from the dataset, so it is more realistic to write Uia(T). Note that this means something a bit magical is happening when an author proposes a functional form for εi(T).
Combining the equations for the observed outcome and the linear models, one gets a decomposition of the observed outcome in terms of covariates, both observed and unobserved, as well as the treatment.
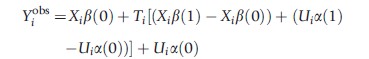
It is standard in econometrics to think of the above model as a regression, where the coefficient on the treatment variable comes from two sources of variation – the first source is the variation due to the observed covariates (Xiβ(1)-Xiβ(0)) and the second is the variation due to the unobserved covariates,(Uia(1)-Uia(0)). It is common to interpret the first source of variation as the gains for the average person with covariate levels Xi, and the second source of variation to be referred to as idiosyncratic gains for subject i. The idiosyncratic gains are the part of this model which allows persons i and j to differ in outcomes even when Xi=Xj.
For reasons laid out in the last subsection, one moves from estimating Di for an individual and instead consider population level parameters. Historically, the quantity of interest for many studies has been the average treatment effect (ATE):
![]()
Note that it is more common to use the conditional ATE:
![]()
This quantity ATE (X) is interpreted as being the expected change in outcome for everyone with characteristics X if they were to go from taking the control to taking the treatment. This is a useful quantity if the researchers are considering a total replacement of a standard treatment (‘control’) with a new treatment (‘treatment’).
Another quantity of interest is the average treatment on the treated (ATT):
![]()
Which is also more usefully thought of as a conditional quantity:
![]()
This quantity limits itself to considering the change in outcomes for only those people who actually received the treatment. The ATT is the pertinent quantity to estimate if people who received the treatment in the dataset are similar to the people who are anticipated to take the treatment in the future. Differences between the ATT and ATE often arise when a new treatment is introduced into a population. As an example, say that a new, more invasive, surgical procedure is introduced as a replacement to a technique which is less invasive, though also believed to be less efficacious. You might imagine that the new technology, because of the acute stress of the procedure, would be used on a relatively healthy subset of the population until the relative efficacy and burdens of the two procedures are well known. Sometimes the difference between the group which receives the treatment is observed and recorded in the covariates. As a simple example of this, let us say the new treatment group has only patients who are less than 40 years old. If this is the case, to estimate the ATE one may have to extrapolate into parts of the overall population for which there are no people who were treated. The problem here is that the efficacy of the treatment may vary for different parts of the population. But if one is not careful to present the estimate as ATT (i.e., appropriate for just a subset of the population) it is quite possible that it will be interpreted as an ATE which may lead to incorrect estimates of the benefit on the entire population. This problem is made even more difficult to address when the treated group is different from the entire population in some unobserved way. See the Sections Methods to Address Selection Bias and Methods for Overt Bias and Bias Due to Omitted Variables on methods for overt bias and bias due to omitted variables for more discussion on this.
Perhaps more is made out of the ATE and ATT distinction than is really necessary. Both of them are discussed in order to make the researcher aware of potential issues of the population of interest and generalizability. Careful thought about the kinds of people who will be impacted by the proposed intervention will typically guide the researcher to the correct choice of either ATE or ATT. For a more exhaustive discussion see Imbens (2004).
Note that ATEs are discussed over populations. These are valuable quantities and are often quite useful for designing policy interventions. But one should point out that it is often plausible that there are subpopulations within the larger group that experience either bigger or smaller treatment effects. This variation in the individual unit’s treatment effect is an important problem and deserves attention, but this issue will not be addressed (except for briefly in the IV and RD sections). The study of ‘treatment heterogeneity’ is gaining attention in the literature and this will add to the usefulness for policy interventions. The quest for ‘personalized medicine’ is in large part an acknowledgment that treatments often vary across subgroups within the population.
Selection Bias
One of the biggest problems with observational studies is that there is selection bias. Loosely speaking, selection bias arises from how the subjects are sorted (or sort themselves) into the treatment or control groups. The intuition here is: the treatment group was different from the control group even before the intervention, and the two groups would probably have had different outcomes even if there had been no intervention at all. Selection bias can occur in a couple of different ways, but one way to write it is
![]()
that is, the joint distribution of the covariates for those who received the treatment is different than for those who received the control. (A bit of a warning: Some confusion may arise when using a conditional statement. This confusion occurs because different academic traditions tend to think of the conditional statement in slightly different ways. For example, a statistician may read a statement like f(X,U|T=1) to mean roughly ‘the joint distribution of X and U when the researcher intervenes and sets T level 1.’ This is in contrast to the way an econometrician may read the statement as, roughly, ‘the joint distribution of X and U limited to those units of observation which were observed to have T=1.’ For a more detailed discussion of what is being asserted in the conditional statement we suggest reading about the ‘do operator’ introduced by Judea Pearl. It is a quite enlightening discussion. See Pearl, 2009 for details.) If this is true, that there is selection bias, then
![]()
This is problematic because the left-hand side of this equation is the unobservable quantity of interest but the right-hand side is made up of directly observable quantities. But it seems like the above equation is used in other settings, namely, experimentation. Why is that acceptable?
In an experiment, because of randomization it is known that
![]()
And it follows that
![]()
Though it is often a dubious claim, many of the standard techniques require an assumption which essentially says that the only selection between treated and control groups is on levels of the observed covariates (X). This is sometimes referred to as overt selection bias. Typically, if overt selection bias is the only form of bias then either conditioning on observed covariates (e.g., by using a regression) or matching is enough to address overt bias. One particular assumption that is invoked quite often in the current health literature is the absence of omitted variables (i.e., only overt bias) and this is used to justify recovering ATT and ATE in some settings. Overt bias will be covered in the propensity score section.
Hidden bias exists when there are imbalances in the unobserved covariates. Let us use the observed outcome formula again, rewriting it like so:
![]()
A least-squares model of Y on T based on the model above will tend to produce biased estimates for E D9X when T is correlated with either Uia(0)or (Uia(1)-Uia(0)). This can arise from unobserved covariates which influence both outcome under both treatment and control and selection into treatment. The resulting bias, referred to as hidden bias, is given by
![]()
Methods To Address Selection Bias
In a randomized experiment setting, inference on the causal effect of treatment on the outcome requires no further assumption than the method for randomizing subjects into the treatment or control (Fisher, 1949). The randomization guarantees independence of assigned treatment from the covariates. And one should pause to stress the point that this independence is for all covariates, both observed and unobserved. By observed covariates it is meant that those covariates which appear in the analyst’s dataset and unobserved all of those that do not. If the sample is large enough then this independence means that the treatment group will have quite similar covariate distribution as the control group. Therefore, any variation noted in the outcome is more readily attributed to the variation in the treatment level rather than variation in the covariates.
The primary challenge to observational studies is that selection into treatment is not randomly assigned. Usually there are covariates, both observed and unobserved, which determine who receives treatment and who receives control. In such a case variation in the outcome is not easily attributable to treatment levels because covariates are different between the different levels as well. There are study designs which were created to address this selection bias and we introduce these methods here. These methods will be classified as (roughly) into two groups: (1) those methods which address only the observed selection bias and (2) those methods which attempt to address selection bias on both the observed as well as unobserved covariates.
Methods Which Address Only Overt Bias
Methods which address selection bias based only on observed covariates tend to be easily implemented, but they also tend to leave the analyst open to major criticism. The assumptions required for the methods in this section are hefty. The authors hope that as the electronic medical records come in to common use; the quality and detail of the covariates available to the health policy researcher will begin to make it more believable that one has access to all of the important covariates. Better quality data is always much appreciated. Better methods can only help so much.
Model-Based Adjustment (E.G., Linear Regression)
Across much of the applied econometric literature, model-based adjustment is the most common method for addressing selection on observed covariates. The most common form of model-based adjustment is linear regression. More complex methods can be developed from maximum-likelihood models, Bayesian hierarchical methods, or other more complex methods. These methods are often designed to estimate the ATE under a powerful assumption. Loosely, one can think of this assumption as saying: selection into the treatment is occurring systematically only on variables which are observed. Formally, this assumption is often written as
![]()
Where ┴ denotes the conditional independence between the treatment and the joint distribution of the counterfactual outcomes. Two random variables are conditionally independent given a third variable if and only if they are independent in their conditional distribution given the conditioning variable. The above assumption, essentially saying one has all the covariates one needs, has a few different names: strongly ignorable treatment assignment (Rosenbaum and Rubin, 1983), selection on observables (Heckman and Robb, 1985), conditional independence, no confounders (in the epidemiology literature), or ‘overt bias’ and ‘the absence of omitted variable bias’ (in the econometrics literature). This article tries to use the ‘overt bias’/‘absence of omitted variable bias’ labels consistently, but please feel free to mentally replace those terms with your favorite.
Propensity Score Methods
Propensity score methods, propensity score matching in particular, have been of particular interest in the health policy literature. It is speculated that the reason for this interest is related to the fact that with propensity score methods it is possible to mimic the feel of the familiar and salient randomized controlled experiment. The propensity score is defined as:
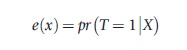
Rosenbaum and Rubin (1983) showed that assuming there is only overt bias, conditioning on the propensity score will lead to independence of the treatment and the potential outcomes. That is,
![]()
This conditioning statement is quite useful; it justifies matching techniques and inverse weighting techniques (see Sections Propensity score matching and Inverse probability weighting). But what is the difference between conditioning on the propensity score and the assumption that there is only overt bias? The assumption, as laid out in the formula above, seems to require that there are two people with exactly the same values of all of their covariates before treatment selection is independent of the potential outcomes. That would mean that if even one covariate value was different between two subjects then one would be concerned that treatment was still being confounded by the covariates, and the treatment estimate would be biased. Finding two identical units of observation is quite difficult (but not impossible, see differencein-differences and before-and-after study designs discussed in Section Before-and-after (difference-in-differences)). The usefulness of the propensity score is that, assuming only overt bias, it shows that one does not need to find identical units merely needed to find units with the same probability of treatment assignment. This makes the analyst’s job easier, because one only requires agreement on the propensity score in order to get a valid estimate of the causal effect. And matching on a one-dimensional feature is more easily accomplished than a high-dimensional vector. Said another way, the propensity score (a scalar) contains all of the requisite information contained in the covariates (often quite high dimensional).
It should be noted that exact matching on the propensity score (i.e., matching individuals i and j such that e(xi) = e(xj)) does not lead to exact matching on the covariates even in infinite samples. This means that the covariates within a pair match are likely to never be exactly the same (i.e., xi≠xj). But what matching on the propensity score does guarantee (asymptotically) is that f(X|T=1)=f(X|T =0). Is this a problem? Having two units of observation which are identical on all of their observed covariates, xi =xj, would be ideal because one could give unit i the treatment and unit j the control and any variation observed in the outcome would be plausibly (we only say ‘plausibly’ because it is still quite likely that there are differences on the unobserved covariates, ui≠uj) attributed to the variation in treatment. But that is not even what happens in a clinical trial. In a clinical trial one may match on important variables, but it is the randomization on which the inference is built. In a randomized trial the joint distribution of the covariates is similarly guaranteed to be equivalent, but the inference requires only that the randomization to be understood. For a discussion of both the relative benefits of exact matching (a.k.a. reducing heterogeneity) and propensity score match (i.e., randomization-based inference), as well as the intellectual history behind these two drives in research, refer to Rosenbaum (2005).
Typically the propensity score is estimated using a logistic regression, though this is not required. Conceivably, other techniques which estimate the probability of treatment given a unit’s covariates would be valid.
Once the propensity score has been estimated there are several ways that it can be used to adjust for selection bias. A very simple technique is to enter the propensity score in the regression estimating the relationship between the treatment and the outcome. In this simple example, the propensity score acts very much like the model-based adjustment methods described in Section Model-based adjustment (e.g., linear regression). (The analyst should be aware that there are a few hefty assumptions required to use the propensity score in the regression framework.) There are other techniques for implementing propensity scores such as propensity score matching and inverse probability weighting. These more sophisticated techniques have distinct advantages when the treatment effect is not equivalent across the entire distribution of the X’s because these methods focus the estimation on the part of the distribution where there is a substantial probability that either treatments might be selected.
Propensity Score Matching
Once the propensity score is estimated, e(x), then units are ideally matched to each other so that treated units with a particular value of e(x) are matched to control units with the same value of the propensity score. It is most common to do pair matching (one treated unit matched to one control unit) though it is also possible to match more than one treated unit to one control, or more than one control unit to one treated unit. (see Hansen, 2004, for more on full matching and K to 1 matching.)
Propensity score matching is often thought of as attempting to replicate a randomized controlled experiment. As such, once matching has taken place it is common to assess the covariate balance between the control and treated units. This is often done using the means of the covariates (citation). Once a properly balanced study design has been achieved, something as simple as a paired t-test is often run to estimate the treatment effect.
Matching also has the benefit of forcing the analyst to be aware of covariate overlap, or lack thereof. In many applications the treatment group and the control groups have different values of the covariates. For example, the control group may have people who are younger than the treatment group – say the youngest person in the treatment group is 50 but half of the control group is less than 30. This is important because part of the assumption of only overt bias, 0<pr (T=1|X)<1, requires there are units at all covariate levels which take on treatment and control. Model-based approaches leave the unaware-analyst at a disadvantage because it is not routine to check for covariate overlap between the treated and control groups. Nonoverlap is a significant violation of a fundamental assumption.
One of the more famous applications of propensity score matching was a study of right heart catheterization – see Connors et al. (1996).
Inverse Probability Weighting
Inverse probability weighting (IPW) takes each unit and weights it by the inverse of the propensity score. That is a weight, suppose we choose w=1/e(x)`, is assigned to each unit of observation. If a unit has a particularly low probability of treatment then the weight will take on a very large value. Once all the observations have been weighted as such, the treatment is independent of the potential outcomes and inference on the treatment effect is trivial. When there are extremely low values of the propensity score (i.e., certain covariate values are strongly associated with selection into the control), the standard errors associated with IPW inference can get quite large. This problem is not unique to IPW methods, matching and regression face similar challenges. There are a number of different estimators based on IPW.
Although uncommon in some health policy settings, inverse probability weighting has been applied to great advantage in epidemiology. Many of the statistical techniques of analysis with IPW can be ported over from the survey sampling literature where sampling weights are heavily used.
Combining Propensity Score Methods And Covariate Adjustment
Rubin (1973) used simulation studies to examine the tradeoffs between model-based approaches and matching-based approaches. Models tended to be more statistically efficient than matching-based techniques, with the significant caveat that this was true with the model was correctly specified (i.e., that the proposed model was exactly the right model for the process which actually generated the data). In fact, if the proposed model is incorrect, then model-based methods may actually exacerbate the bias. Matching-based methods were shown to be fairly consistent in reducing overt bias. The study concluded that a combination of the two methods produced estimates which were both robust and efficient. A diligent analyst, with strong justification for a specific model, may first match to ensure covariate overlap between the treated and control and then run the model-based inference on the subjects which were part of the matching.
Methods For Overt Bias And Bias Due To Omitted Variables
Regression, propensity score matching and any methods predicated on only overt bias do not address selection on unobserved covariates. It is important to be aware of this because a well-informed researcher needs to judge if available covariates are enough to make a compelling argument for the absence of omitted variables. This is often a dubious claim because (1) a clever reviewer will usually find several variables missing from your dataset and/or (2) there are ‘intangible’ variables that are difficult, or perhaps inconceivable, to measure. The following study designs are presented below in order to help you address these situations.
It is important to note that none of the designs below come ‘for free,’ that is without some hefty assumptions. It is important to consider these assumptions carefully before proceeding.
Instrumental Variables
An instrumental variable (IV) design takes advantage of some randomness which is occurring in the treatment assignment to help address imbalances in the unobserved variables. IV methods go beyond simple methods (like propensity score or multivariate regression) which are only designed to address imbalances in observed covariates.
An instrument is a haphazard nudge toward acceptance of a treatment that affects outcomes only to the extent that it affects acceptance of the treatment. In settings in which treatment assignment is mostly deliberate and not random, there may nevertheless exist some essentially random nudges to accept treatment, so that use of an instrument might extract bits of random treatment assignment from a setting that is otherwise quite biased in its treatment assignments. Holland (1986) offers an intuitive introduction to how an ideal IV would work. Angrist et al. (1996) used the potential outcomes framework to bring greater clarity to the math of IV.
This intuition for IV discussed above enhances the classic econometric presentation of IVs where the focus is on correlation with the error term. To introduce this more formally, the authors will introduce the ‘complier terminology’ from Angrist et al. (1996).
Notation first: Z is used to denote the instrument. If these random variables have subscripts one is referring to an individual’s values. If the random variables are in bold then one is referring to the vector of values for all observations in our dataset. This section will assume that the treatment is binary (i.e., Ti=1 if the ith unit takes the treatment and Ti=0 otherwise) and that the instrument is binary (i.e., Zi=1 if the ith unit is encouraged to take the treatment and Zi=0 otherwise). The notation Ti(z=1) is used to denote the treatment that the ith unit actually receives if encouraged, z=1, to take the treatment.
The story goes, the instrument either encourages the unit to receive the treatment (Zi=1) or not (Zi=0). The unit is then allowed to either comply with that encouragement or not. Because both the treatment and the instrument are assumed to be binary, it follows that there are four compliance classes. Using counterfactuals, the authors label these compliance classes like so:
- Always takers: Ti(Zi=1)=Ti (Zi= 0)=1
- Compliers: Ti (Zi=1)=1,Ti (Zi= 0)= 0
- Never takers: Ti (Zi =1) =Ti (Zi= 0) = 0
- Defiers: Ti (Zi=1) =0,Ti(Zi =0)=1
Under any possible random assignment of the instrument one will never be able to discern the treatment effect for the always-takers nor the never-takers because no matter what one will never be able to observe the counterfactual treatment assignment. Assumption 4 (monotonicity) says that the defiers do not exist. Thus one is only able to estimate the treatment effect for the compliers, those who are randomly assigned by the instrument. This estimand is often referred to as the local average treatment effect (LATE) because it is only true for a subpopulation (a ‘local’ group). It has also been referred to as the complier average causal effect (CACE). CACE is a special case of LATE; CACE is often used when the treatment and instrument are binary. LATE is more broadly defined. A more fundamental estimand, the local instrumental variable (LIV), can be derived from the use of an instrument. The LIV is capable, assuming the proper specification of the model and proper weighting of population covariates, of estimating the ATE and TT (Heckman and Vytlacil, 1999, 2000). Thus the LIV is a useful tool which allows the analyst to shift between estimating effects on different parts of a populations.
An instrument is weak if the random nudges barely influence treatment assignment or strong if the nudges are often decisive in influencing treatment assignment. Another way to think of a ‘strong’ versus ‘weak’ instrument is to think of the percentage of compliers. A strong instrument will induce higher rates of compliance. A study with a weaker instrument will have a lower percentage of compliers. Although ideally an ostensibly random instrument is perfectly random and not biased, it is not possible to be certain of this; thus a typical concern is that even the instrument might be biased to some degree. It is known from theoretical arguments that weak instruments are invariably sensitive to extremely small biases – Bound et al. (1995); for this reason, strong instruments are preferred.
The most common method for implementing IV is two-stage least squares (2SLS). 2SLS is valid when the outcome of interest is continuous, and all of the typical model requirements for least squares are met. If the instrument is binary and the outcome is linear, then the 2SLS estimate is the Wald estimator (Angrist, 1991). If the outcome of interest is something other than nonlinear then there are a couple of other methods available. The two methods the authors cite are both rather new to the literature and are only beginning to work their way into use. Two-stage residual inclusion (2SRI) method is a parametric method for dealing with nonlinear outcomes (Terza et al., 2008). Near/far matching is a nonparametric method that attempts to replicate the structure of a randomized controlled experiment (Baiocchi et al., 2010). Near/far matching may feel a bit similar to propensity score matching, with the addition feature of taking into account the randomness from the instrument.
As laid out in Angrist et al. (1996), there are five assumptions for IV when you have a binary instrument and a binary treatment. This is a bit surprising to some folks because we typically only discuss two assumptions. The two assumptions from econometrics are broken apart into assumptions 1, 2, and 3 below. Assumptions 1 and 2 are often combined. Assumptions 4 and 5 are often overlooked in the literature. All of these assumptions are important and thus need to be justified before an IV analysis is to be taken seriously.
(1) Uniform Random Assignment
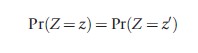
for all possible treatment assignments z and z` such that 1Tz =1Tz` , where 1 is the N-dimensional column vector with all elements equal to one.
This assumption guarantees that the instrument (Z) is randomly assigned, it says nothing directly about the treatment actually received. This assumption can be restated such that the probabilities are conditional on the observed covariates. See the section on ‘Instrumental Variables – Complier Terminology.’
(2) No direct effect of the instrument on the outcome (Angrist et al. (1996) refers to this as this assumption as the ‘exclusion restriction,’ which may be a bit confusing given the use of this term in the econometrics literature to refer to both assumptions 1 and 2 in the Angrist et al. (1996) framework.)
![]()
Intuitively, this assumption says that the instrument has no impact on the outcome except through the instrument’s influence on which treatment the unit actually receives. There are a number of ways to violate this assumption. One way this would be violated is in the study of a treatment if there is reason to believe in a ‘placebo effect’ – whereby merely believing in the treatment has an effect – where the unit will have a different outcome based merely on whether being assigned to take the treatment or not, rather than through the actual treatment taken. This assumption is quite important and is often a source of difficulty in justifying the validity of an IV method.
(3) Nonzero Average Causal Effect of Z on T.
The average causal effect of Z on T, E[Ti(Zi =1)- Ti(Zi = 0) is not equal to 0.
This assumption ensures that the instrument actually has an impact on the treatment. If the instrument does not change the probability of the treatment assignment, then the instrument is useless because one cannot harness any of the randomization from the instrument to examine the effect of the treatment on the outcome. Note that the average causal effect is estimating the percentage of compliers. If there are more compliers in the study, then one has a stronger IV. If this connection between the instrument and the treatment received is weak then serious problems can arise – see Bound et al. (1995) for a discussion on weak instruments.
(4) Monotonicity
![]()
The monotonicity assumption means that the instrument must either encourage units to take the treatment or discourage units from taking the treatment, it cannot have both effects. The monotonicity assumption says that the defiers – those who do exactly the opposite of what they are encouraged to do – are not present in our study. This is an interesting addition to the literature.
(5) Stable Unit Treatment Value Assumption (SUTVA):
![]()
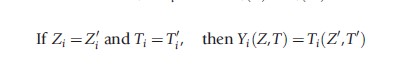
SUTVA implies that the potential outcomes for each person i are unrelated to the treatment status of other individuals. This assumption means that settings in which one unit’s treatment assignment impacts another unit’s outcome are outside of our investigative range. Some examples of tricky situations: immunizations because the probability of unit i being infected depends on how many immunized people there are in the community (i.e., ‘herd immunization’) and the effect of academic ability from a teacher on a student is tricky to identify because students will learn from peers who potentially receive instruction from other teachers.
Some informal thoughts about the IV assumptions: Assumption 1 (Uniform Random Assignment) is challenging to defend because the assumption is about unobserved quantities. One method for reassuring the reviewer that Assumption 1 is at least plausible is by checking to see if the observed covariates look reasonably random across the different values of the instrument. This is not a guarantee of the randomness of the instrument (nor is it technically a disproval), but it is perhaps reassuring. Assumption 2 is sometimes dubious and will be a point of contention if the reviewer is clever. Assumption 3 is testable from the data because the association is observable in the data. Assumption 4 is often feasible; see the ‘complier’ terminology below to see why. Assumption 5 (SUTVA) is most often violated in studies involving infectious disease and settings where there is a ‘spillover’ effect from one subject to another.
Heterogeneity And Compliance Classes
If the treatment is believed to affect people differently, then it is possible that the compliance classes can be thought of as arising from heterogeneity. It is likely that the always-takers know they will benefit from the treatment, possibly more than others. The never-takers possibly have lower expected benefit. And the compliers would have an unknown level of benefit. This is not necessarily how things work in an example, but is a plausible enough scenario to show that estimating LATE is likely to be different than estimating ATE. The analyst needs to be aware of this issue. The estimate that we get from an IV analysis is only on a subset of the population, and perhaps this subset of the population is not representative of the overall population.
A few examples of an instrument in the medical literature: travel time to treatment facility (McClellan et al., 1994), regional variation in treatment practices (Hadley et al., 2003), and for drug utilization the instrument of prior patient’s drug prescription (Brookhart et al., 2006).
Regression Discontinuity
Regression discontinuity (RD) designs take advantage of an abrupt difference in treatment assignments. An example: say we are interested in the effects of a new blood pressure drug. An RD design might be available if there were protocols for treatment selection based on weight. Let us say that there was a policy requiring that anyone lesser than 70 kg is ineligible for the new drug. It might be possible, if physicians and patients strictly adhere to this policy, that the patients who weigh 69.5 kg and the patients who weigh 70.5 kg are actually quite similar in terms of their important covariates but face quite different prospects for receiving the new blood pressure medicine.
RD designs can be thought of as a special case of IVs, where the analyst has a dichotomized instrument (i.e., whether the subject is above or below the discontinuity). Like an IV design, the assumption of random assignment to the levels of the treatment needs to be discussed. Continuing with the blood pressure medicine example, one might justify the 70 kg cut-off as being similar to random assignment because (1) the scales are likely to have measurement error, (2) patients’ weights can vary throughout the day, and (3) the method for weighing (e.g., with clothing or without) will impact the patient’s estimated weight. These arguments help with Assumption (1) for the IV assumptions, but the other assumptions need to be similarly addressed.
Often an RD estimate is valid for only those people who are ‘near’ the discontinuity. In the example, it is likely that one is looking at similar patients if one is considering people who are 69–69.9 kg versus 70.1–70.9 kg. However, it seems likely that the groups defined by 50–69.5 kg and 70.5–90 kg are quite different. This is a case of LATE, where the compliers are additionally restricted to some neighborhood around the discontinuity point. The authors have heard this estimand referred to (in jest) as ‘very LATE.’
Before-And-After (Difference-In-Differences)
The before-and-after and the difference-in-differences (DiD) methods are common techniques to address the possibility that there are unobserved covariates which are causing confounding. Both techniques take advantage of multiple measurements taken at different periods in time. These techniques have been used to great benefit – see Card and Krueger (1994). Both are important techniques in the field, but the authors will do little more than mention them here. For a more detailed discussion the authors recommend looking in standard econometric textbooks for ‘panel data’ techniques.
Sensitivity Analysis
In one sense sensitivity analysis is a ‘meta’ method because it functions as an analysis of the results of an already existent analysis. The researcher must first select a method, possibly one of the methods described in Sections Methods to Address Selection Bias and Methods for Overt Bias and Bias Due to Omitted Variables, and then perform a sensitivity analysis on that. Acknowledging that the assumptions are just that, merely assumptions, a sensitivity analysis will reanalyze the analysis considering violations of the assumptions occur. A general formulation of a sensitivity analysis is difficult, because it is dependent on the underlying method of analysis. But sensitivity analysis offers a powerful tool for observational studies to explore the effect of the assumptions necessary to make a causal interpretation of the data analyzed.
In an experiment, the randomization to treatment or control allows the researcher to address unobserved variation. In observational studies, the analyst is forced to rely on assumptions to address unobserved variation. Again, the clever reviewer knows how to come up with plausible scenarios and variables which will invalidate the assumptions required to use the method you are employing. (This is not unique to observational studies, in experimental settings it is often called into question whether or not the experimenters did the proper kind of adjustments and randomization in order to truly randomize the experimental subjects.) The good thing about a sensitivity analysis is that it switches the burden of defending your analysis from a case-by-case defense against each possible scenario and instead moves the argument to an order of magnitude (e.g., yeah, each of these arguments are interesting, but they would need to increase selection into the treatment group by a factor of 5 and at the same time increase the rate of death by four times).
A detailed description of sensitivity analyses can be found in Rosenbaum (2002, Chapter 4). Note that a sensitivity analyses will only indicate the magnitude of hidden biases that would alter a study’s conclusions but does not address how to overcome these biases.
Example Revisited
NICUs have been established to deliver high-intensity care for premature infants (those infants born before 37 weeks of gestation). If one looks at all of the preemies that were delivered in Pennsylvania between 1995 and 2005, it is seen that 2.26% of the preemies delivered at high-level NICUs died whereas only 1.25% of the preemies who were delivered at low-level NICUs died. No one believes the difference in outcomes reported above is solely attributable to the difference in level of intensity of treatment. People believe it is due to difference in covariates. Based on the observable covariates, this is plausible because it is seen that preemies delivered at high-level NICUs weighed approximately 250 g less than the preemies which were delivered at low-level NICUs (2454 at high-level NICUs vs. 2693 at low-level NICUs). Similarly preemies delivered at high-level NICUs were born a week earlier than their counter parts at low-level NICUs on average (34.5 vs. 35.5 weeks). If you perform a propensity score matching using the observed covariates then the analysis will give you an estimate saying that there is a reduction of 0.05% of deaths if the preemies were to be delivered at high-level NICUs. Inverting a paired t-test, the confidence interval for this goes from ( 0.05%, 0.15%), and is thus an insignificant result. This is meaningful result for policy if the assumption of overt bias only, which is a necessary assumption in propensity score matching, holds in this example.
But one does not have access to medical records. One only has access to health claims data. It is quite likely one does not have all necessary covariate in our dataset, so assuming only overt bias is likely to lead to biased estimates. To attempt to deal with this problem Baiocchi et al. (2010) used an IV approach. They used distance to treatment facility as an instrument, because travel time largely determines the likelihood that mother will deliver at a given facility but appears to be largely uncorrelated with the level of severity a preemie experiences. Using this approach Baiocchi et al. (2010) estimated a CACE of 0.9% with a confidence interval of (0.57%, 1.23%). Be aware that the authors are estimating a different parameter. It is only appropriately thought of as estimating for a subset of the population, so one cannot readily compare the two estimates. But it is suggestive to note the larger estimated effect, as well as the significance of the result.
You should not walk away from this example thinking that IV methods are always preferred over propensity score matching methods. That is most definitely not the point here. But you should be aware that there are several different methods out there, and you should be comfortable thinking about what is the appropriate method to use in a given situation. In the NICU example, because one only has access to medical claims data – instead of medical charts – it is likely one is missing covariates that would inform us about what we believe to be important selection bias. Given that, one needs to use some method to address the unobserved selection bias, above and beyond the approaches one used to deal with the observed selection bias.
Bibliography:
- Angrist, J. (1991). Grouped-data estimation and testing in simple labor-supply models. Journal of Econometrics 47, 243–266.
- Angrist, J. D., Imbens, G. W. and Rubin, D. B. (1996). Identification of causal effects using instrumental variables (with Discussion). Journal of the American Statistical Association 91, 444–455.
- Baiocchi, M., Small, D., Lorch, S. and Rosenbaum, P. (2010). Building a stronger instrument in an observational study of perinatal care for premature infants. Journal of the American Statistical Association 105, 1285–1296.
- Bound, J., Jaeger, D. A. and Baker, R. M. (1995). Problems with instrumental variables estimation when the correlation between the instruments and the endogenous explanatory variable is weak. Journal of the American Statistical Association 90, 443–450.
- Brookhart, M. A., Wang, P. S., Solomon, D. H. and Schneeweiss, S. (2006). Evaluating short-term drug effects using a physician-specific prescribing preference as an instrumental variable. Epidemiology 17(3), 268–270.
- Card, D. and Krueger, A. (1994). Minimum wages and employment: A case study of the fast-food industry in New Jersey and Pennsylvania. American Economic Review 84(4), 772–793.
- Connors, A., Speroff, T., Dawson, N., et al. (1996). The effectiveness of right heart catheterization in the initial care of critically ill patients. Journal of the American Medical Association 276, 889–897.
- Cox, D. R. (1958). Planning of experiments. New York: John Wiley. Fisher, R. A. (1949). Design of experiments. Edinburgh: Oliver and Boyd.
- Hadley, J., Polsky, D., Mandelblatt, J., et al. (2003). An exploratory instrumental variable analysis of the outcomes of localized breast cancer treatments in a Medicare population. Health Economy 12, 171–186.
- Hansen, B. (2004). Full matching in an observational study of coaching for the SAT. Journal of the American Statistical Association 99(467), 609–618.
- Heckman, J. and Robb, R. (1985) Alternative methods for evaluating the impacts of interventions. In Heckman, J. J. and Singer, B. (eds.) Longitudinal analysis of labor market data. New York: Cambridge University Press.
- Heckman, J. and Vytlacil, E. (1999). Local instrumental variables and latent variable models for identifying and bounding treatment effects. Proceedings of the National Academy of Sciences 96, 4730–4734.
- Heckman, J. and Vytlacil, E. (2000). The relationship between treatment parameters within a latent variable framework. Economic Letters 66, 33–39.
- Hernan, M. A. and Robins, J. M. (2013). Causal inference. Chapman & Hall. Available at: https://www.hsph.harvard.edu/miguel-hernan/causal-inference-book/.
- Holland, P. (1986). Statistics and causal inference. Journal of the American Statistical Association 81(396), 968–970.
- Imbens, G. (2004). Nonparametric estimation of average treatment effects under exogeneity: A review. Review of Economics and Statistics 86(1), 4–29.
- McClellan, M., McNeil, B. J. and Newhouse, J. P. (1994). Does more intensive treatment of acute myocardial infarction reduce mortality? Journal of the American Medical Association 272(11), 859–866.
- Neyman, J. (1990). On the application of probability theory to agricultural experiments. Statistical Science 5, 463–480.
- Pearl, J. (2009). Causality: models, reasoning, and inference, 2nd Cambridge: Cambridge University Press.
- Rosenbaum, P. (2002). Observational studies, 2nd ed. New York: Springer.
- Rosenbaum, P. (2005). Heterogeneity and causality: Unit heterogeneity and design sensitivity in observational studies. American Statistician 59(2), 147–152.
- Rosenbaum, P. and Rubin, D. (1983). The central role of the propensity score in observational studies for causal effects. Biometrika 70(1), 41–55.
- Rubin, D. B. (1974). Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology 66, 688–701.