Introduction
Decision-modeling is increasingly used or required by health technology funding/reimbursement agencies as a vehicle for economic evaluation. The process of developing and analyzing a decision analytic model as part of a health technology assessment (HTA) involves many uncertainties. Some relate to the assumptions and judgments regarding the conceptualization and structure of a model, others to the quality and relevance of data used in the model. Where data are absent or inadequate to inform model uncertainties, the decision maker is faced with the options of using whatever data are available, or commissioning and/or waiting for further research. Delaying a decision is not without negative consequences, however, as patients may not receive what is actually the most cost effective intervention and population health will be negatively affected. As an alternative to delaying decisions, eliciting expert opinion can be useful to generate or complement the missing evidence.
Elicitation can transform the subjective and implicit knowledge of experts into quantified and explicit data. Characterizing experts’ uncertainty over the elicited values of parameters further used within a decision model, and assessing the consequential impact on decision uncertainty, is particularly important in HTA. It is also useful in exposing disagreements and different degrees of uncertainty among experts. By specifying the ‘current level of expert knowledge’ as distributions, these can be used to generate estimates of the value of conducting further research to resolve these uncertainties.
There are many possible uses for elicitation in HTA (Box 1). In general, it is relevant where otherwise less informed, implicit or explicit assumptions have to be made. Expert knowledge can, therefore, help to characterize uncertainties that otherwise might not be explored.

Techniques for eliciting uncertain quantities have received a lot of attention in Bayesian statistics. However, it is a relatively new technique in HTA and there are few examples of its use. This article attempts to distill a large literature so as to outline the methods available and their applicability to HTA, using relevant examples from the field. It is not intended to be a comprehensive summary but is instead a general guide with further reading for those wishing to dig deeper.
The stages of an elicitation are divided into: the design of the exercise, its conduct, methods for synthesizing data from multiple experts, and assessments of adequacy of the exercise.
The Design Process
Decisions on what quantities to elicit and how to do it should be determined by the intended purpose. There are a number of issues to consider, and these can be categorized as: whose beliefs to collect, what and how to elicit, and specificities of elicit complex parameters such as beliefs regarding correlation.
Whose Beliefs?
There is a large literature on the selection of experts. The criteria range from citations in peer reviewed articles to membership of professional societies. There is no consensus on the best approach. It is generally agreed that an expert should be a substantive expert in the particular area. However, the issue of whether an expert should possess any particular elicitation skills (e.g., previous experience of elicitation) is less clear and will depend on the complexity of the task. Experts with statistical knowledge may be required for elicitation of quantities such as population moments or parameters of statistical distributions, though most experts can be assumed to provide reasonable estimates of observable quantities, such as proportions. In selecting experts, ideally only those without competing interests should be chosen so as to reduce motivational bias. Once the analyst has selected the expert group, one needs to decide how many experts to include in an exercise. Generally, multiple experts will provide more information than a single expert; however, there is a lack of guidance regarding the appropriate number of experts.
What To Elicit?
Although previous elicitations have often sought to elicit probabilities or numbers of events, costs, quality of life weights, and views on relative effectiveness can also be elicited. Once the analyst has decided on the parameters to elicit, the methods of doing so come to the fore. There are several methods available. When eliciting, for example, a transition probability, experts can be asked to indicate their beliefs regarding the probability itself, the time required for x% patients to experience the event, or the proportion of patients who would have had experienced the event after y amount of time. In other words, conditional on particular assumptions, evidence on each of these aspects can inform the same parameter. In selecting an appropriate method, there is a need to consider the compatibility of the format with that of other evidence in the model to be used jointly with the elicited judgments. Where multiple parameters are to be elicited, the analyst may promote some homogeneity in the quantities used, avoiding, for example, seeking judgments on transition probabilities by using proportions of patients for some parameters and the time required for x% patients having had experienced the event for others. It is also generally accepted that experts should neither be asked regarding unobservable quantities nor regarding moments of a distribution (except possibly, the first moment, the mean) or coefficients for covariates.
How To Elicit?
After choosing which quantities to elicit, the expert needs to be able to express his/her uncertainty over each. Previous applications of elicitation techniques have found that nonnumerical expressions of uncertain quantities can be useful. However, obtaining quantitative rather than qualitative judgments on the level of uncertainty is required in a decision model. This is usually done by asking experts to specify their beliefs over a manageable number of summaries characterizing their uncertainty surrounding the quantity of interest. Ideally, the focus should be on eliciting summaries with which the experts are familiar and it is generally agreed that experts do not perform well when asked directly to provide estimates of variance. It can also be useful to elicit quantities that are conditional on observed or hypothetical data.
Experts can be asked to reveal credible intervals directly (the range of values that an expert believes to be possible within a specified degree of credibility, usually 95%) or other percentiles of the distribution. Variable interval methods can be used, where percentiles are prespecified and the expert is asked to indicate intervals of values in accordance with their beliefs regarding the particular parameter. Alternatively, the fixed interval method, which is also based on percentiles, requires the analyst to specify a set of intervals that a specific quantity X can be contained within. The expert then gives the probability that X lies within each interval.
A method that has been applied previously in HTA is the histogram technique or probability grid. This is a graphical derivation of the fixed interval method where the expert is presented with possible values (or ranges of values) of the quantity of interest, displayed in a frequency chart on which he/she is asked to place a given number of crosses in the intervals or ‘bins’. Histograms are appealing to even the least technical of experts (see Box 2 for an example of this method in practice).
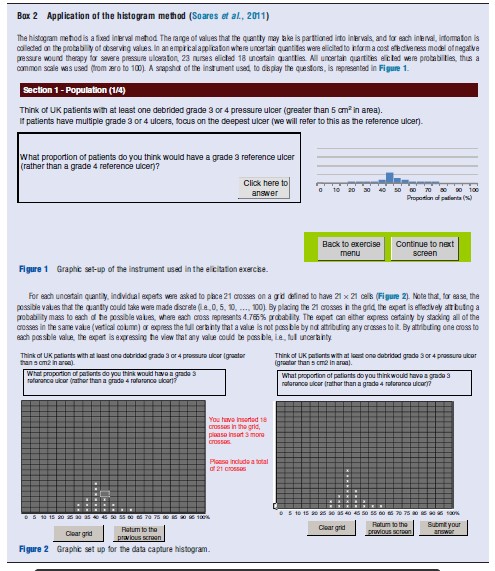
Eliciting Complex Parameters
Complex parameters include joint and conditional quantities, regression parameters, and correlation, and transitions in a multistate model (e.g., a Markov model). Perhaps the most common challenge arising with parameters that are interdependent is that a joint distribution may need to be elicited. The analyst can assess the model’s sensitivity to variations in the correlation coefficient, or estimate the correlation as part of the elicitation exercise. There are a number of methods for eliciting correlations but no consensus regarding the most appropriate method. The methods include descriptions of likely strength of correlation, direct assessment, and the specification of a percentile for quantity X contingent on a specified percentile for quantity Y. However, the complexity of eliciting probability distributions that is conditional on other probability distributions is likely to be too cognitively difficult for many experts. In these circumstances, it may be appropriate to adopt a second best approach and elicit distributions conditional on means or best guesses. This was the approach used by Soares et al. (2011), where experts were first asked to record the probability (and uncertainty) of a patient’s pressure ulcer being healed when they received treatment with hydrocolloid dressing. For experts who believed that the effectiveness of other treatments was different from the hydrocolloid dressing, the distribution of the relative treatment effects was elicited by asking experts to assume that the value they believe best represented their knowledge about the effectiveness of the comparator treatment, hydrocolloid dressing, was true (Bibliography: value). The Bibliography: value was the mode (or one of multiple modes, selected at random).
Conducting The Exercise
Explaining The Concept Of Uncertainty
Eliciting measures of uncertainty can be complicated, particularly because one wants to ensure that data reflect uncertainty in the expected value rather than its variability or heterogeneity. This is largely a question of the format of the exercise; however, it can also be useful to present contrasting examples of uncertainty and variability to help the expert understand the key distinctions. Visual aids (such as the histogram) can be useful for the elicitation exercise and can help to reduce the burden on experts. It is also helpful to train them, especially when they have limited experience of elicitation. Experts will often respond better to questions and give more accurate assessments if they are familiar with the purpose and methods used in the elicitation exercise. Frequent feedback should also be given during the process and, if possible, experts should be allowed to revise their judgments.
Understanding The Impact Of Bias And The Impact Of Heuristics
It can be useful to understand how experts judge unknown quantities, in particular, whether they use specific principles or methods in order to make the assessment of probability simpler. These heuristics are useful but can sometimes lead to systematic errors. Garthwaite et al. (2005) described the following heuristics: judgment by representativeness, judgment by availability, judgment by anchoring and adjustment, conservatism, and hindsight bias. All these issues should be considered when eliciting probabilities, as each can bias the assessments derived from experts, although the direction of bias is unlikely to be known. In addition, any motivational biases, bias from operational experience, and confirmation biases must be considered and appropriate measures taken to address their implications. Examples of biases in elicitation are described in Box 3.

Synthesizing Multiple Elicited Beliefs
When judgments from several experts are required, it is often desirable to obtain a unique distribution that reflects the judgments of all of them. There are two broad methods for achieving this: behavioral and mathematical.
Behavioral approaches focus on achieving consensus. A group of experts is asked jointly to elicit its beliefs, as if it were a single expert, through the implicit synthesis of opinion and without aggregating individual opinions. In this approach, experts are encouraged to interact in order to achieve a level of agreement for a particular parameter. There are a number of behavioral aggregation techniques. The Delphi technique is probably the best known of these and it has been frequently applied to decision-making in healthcare. It involves sequential questionnaires interspersed by feedback and has characteristics that distinguish it from conventional face-to-face group interaction, namely, anonymity, iteration with controlled feedback and statistical response. The Nominal Group Technique is another popular consensus method. Here individuals express their own beliefs to the group before updating these on the basis of group discussion. The discussion is facilitated either by an expert on the topic or by a credible nonexpert. The process is repeated until a single value (or distribution) is produced.
However, there are problems with group consensus. First, consensus may not be easily achieved, and in some circumstances, there may be no value that all experts can agree on. Second, dominant individuals may so lead a group that they effectively determine the view of the whole group. Perhaps most importantly, however, is that a focus on achieving consensus means that behavioral approaches miss the inherent uncertainty in experts’ beliefs regarding a parameter. There is a tendency for the group to be overconfident when reaching consensus regarding an unknown parameter.
Mathematical approaches to synthesizing multiple beliefs do not attempt to generate a consensus. Rather, they focus on combining individual beliefs to generate a single distribution using mathematical techniques. Aggregating individual experts’ estimates into a single distribution is the preferred approach in applied studies. However, some studies have also used individual experts’ assessments as separate scenarios for exploration. Synthesis of data from multiple experts often involves two steps: fitting probability distributions and combining probability distributions.
Fitting Probability Distributions
Fitting probability distributions to elicited data can be undertaken by the analyst either post elicitation or by asking the experts to assess fitting as part of the elicitation exercise. Parametric distributions can be fitted if an expert’s estimates can be represented in such a way. The choice of parametric distribution is usually governed by the nature of the elicited quantities. If elicited priors are to be updated with sample information, then choosing conjugate distributions is advantageous for analytical simplicity. However, the development of computational methods has made it possible to choose nonconjugate distributions (i.e., distributions not from the same statistical family). Nonparametric methods can also be used. These do not assume that the data structure can be specified a priori; in effect, they have an unknown distribution.
Combining Probability Distributions
There are two main methods for combining probability distributions: weighted combination and Bayesian approaches. Weighted combination is referred to as opinion pooling, more specifically either linear opinion pooling or logarithmic opinion pooling. If p(θ) is the probability distribution for unknown parameter θ, in linear pooling, experts’ probabilities are aggregated using the simple linear combination: p(θ)=∑iωi·pi(θ), where wi represents a weight assigned to expert i. In logarithmic opinion pooling, averaging is undertaken using multiplicative averaging. These two methods can differ greatly, with the logarithmic method typically producing a narrower distribution for the parameter, implying less uncertainty in the estimate.
An example of the use of linear pooling is described by White et al. (2005), they have elicited expert opinion on treatment effects and the interaction between three trials. Experts are asked to assign a weight of belief (up to 100) to intervals of annual event rates. Experts’ weights were then combined by taking the arithmetic mean of individual assessments (linear pooling with equal weighting of experts).
More recently, there has been a move toward using Bayesian models for combining probabilities. Aggregation in a Bayesian model uses the experts’ probability assessments to update the decision makers’ own prior beliefs regarding an uncertain parameter. These methods have not yet been applied in HTA and the need for the decision makers’ input is likely to be difficult to implement in practice.
If experts have been asked to express their beliefs regarding the value of an unknown quantity using a histogram, number of options are available for aggregation. Linear opinion pooling and Bayesian models can be used to aggregate parametric distributions, fitted to each expert’s histogram. Alternatively, the empirical distributions derived can be combined to generate one overall empirical distribution.
Interdependence Of Experts
Regardless of the method used to combine experts’ probability distributions, an additional level of complexity is introduced when the assumption that experts provide independent beliefs is not sustainable. This is more likely if experts are chosen from the same professional organization or base their beliefs on shared experience or information. In this case, joint distributions should be used, incorporating the covariance matrix for the experts’ assessments.
Assessing Adequacy
Four alternative measures have previously been described in the literature for assessing the adequacy of an elicitation: internal consistency, fitness for purpose, scoring rules, and calibration.
Internal Consistency
Internal consistency is particular relevant when eliciting probabilities. An expert’s assessment of one (or more) unknown parameters should be consistent with the laws of probability. Achieving coherence may, however, involve more complex reasoning and, in the presence of such complexity, either incoherent judgments are transformed for further use or the exercise is constructed in order to minimize or eliminate incoherence. Qualitative feedback can also be useful in assessing internal consistency. Any discrepancies can be fed back to the experts and appropriate adjustments to assessments can be made.
Fitness For Purpose
Inevitably, some degree of imprecision will remain in elicited beliefs and their fitted distributions. Sensitivity analysis can be useful in discovering whether the ultimate results of the analysis change if alternative (but also plausible given the expert’s knowledge) distributions are used. A commonly used sensitivity analysis in a Bayesian framework explores alternative prior distributions. If results do not change appreciably, then the distributions can be said to represent the experts’ knowledge and are thus fit for purpose.
Scoring Rules
For parameters that are known or subsequently become known to analysts, comparisons can be made between elicited distributions and those known distributions. This provides an opportunity for assessing the ‘closeness’ of the elicited and actual distributions. The ‘scoring rule’ then attaches a reward (a score) to an expert using some measure of accuracy, with those gaining higher scores being regarded as performing better. Commonly used scoring rules are the quadratic, logarithmic, and spherical methods. In the example from Chaloner et al. (1993), elicitation was used to inform a model using the intermediate results of a randomized trial. On completion of the trial, comparisons were made between elicited estimates and those based on actual data. It was concluded that the elicitation exercise, although producing some thought-provoking results, did not necessarily predict trial outcomes with much accuracy. Although not done explicitly as part of the exercise, it would have been possible to score experts’ beliefs retrospectively, possibly with a view to combining these with the experimental data.
Calibration
The most commonly used method for assessing the adequacy of elicitation is to measure experts’ performance through calibration. The basic premise of calibration is that a perfectly calibrated expert should provide assessments of a quantity that are exactly equal to the frequency of that quantity. By asking experts to provide estimates of known parameters, their performance, in terms of distance between their estimates and the true value, can be determined. Unlike scoring rules, measures of performance such as calibration can then be used to adjust estimates of future unknown quantities. Alternatively, a recent example by Shabaruddin et al. (2010), used the mean number of relevant patients to derive a weighting for each expert. This was then used to generate weighted means in the linear pooling.
Discussion
Formally elicited evidence to parameterize HTA decision models is yet to be used widely. However, it has huge potential. Compared with many other forms, elicitation also constitutes a reasonably low cost source of evidence. However, the potential biases in elicited evidence cannot be ignored, and due to its infancy in HTA, there is little guidance to the analyst who wishes to conduct a formal elicitation exercise.
This article has summarized the main choices that an analyst will face when designing and conducting a formal elicitation exercise. There are a number of issues, of which the analyst should be particularly mindful, especially the need to characterize appropriately the uncertainty associated with model inputs and the fact that there are often numerous parameters required, not all of which can be defined using the same quantities. This increases the need for the elicitation task to be as straightforward as possible for the expert to complete.
There are numerous methodological issues that need to be resolved when applying elicitation methods to HTA decision analysis. In choosing to use more complex methods of elicitation, it is also important to note that the complexity of many HTA decision models and the need to capture experts’ beliefs, as inputs into these, creates a tension between generating unbiased elicited beliefs and populating a decision model with usable parameters. However, where experimental evidence is sparse, controversial, and difficult to collect, as far as emerging technologies, the need to explore the added value of elicited evidence seems particularly pressing.
Bibliography:
- Chaloner, K., et al. (1993). Graphical elicitation of a prior distribution for a clinical trial. Special Issue: Conference on practical Bayesian statistics. Statistician 42(4), 341–353.
- Garthwaite, P. H., Kadane, J. B. and O’Hagan, A. (2005). Statistical methods for eliciting probability distributions. Journal of the American Statistical Association 100(470), 680–700.
- Shabaruddin, F. H., et al. (2010). Understanding chemotherapy treatment pathways of advanced colorectal cancer patients to inform an economic evaluation in the United Kingdom. British Journal of Cancer 103, 315–323.
- Soares, M. O., et al. (2011). Methods to elicit experts‘ beliefs over uncertain quantities: Application to a cost effectiveness transition model of negative pressure wound therapy for severe pressure ulceration. Statistics in Medicine 30(19), 2363–2380.
- White, I. R., Pocock, S. J. and Wang, D. (2005). Eliciting and using expert opinions about influence of patient characteristics on treatment effects: A Bayesian analysis of the CHARM trials. Statistics in Medicine 24(24), 3805–3821.
- Bojke, L., et al. (2010). Eliciting distributions to populate decision analytic models. Value in Health 13(5), 557–564.
- Cooke, R. M. (1991). Experts in uncertainty: Opinion and subjective probability in science. New York: Oxford University Press.
- Jenkinson D. (2005) The elicitation of probabilities – A review of the statistical literature. BEEP Working Paper. Department of Probability and Statistics, Sheffield: University of Sheffield.
- Leal, J., et al. (2007). Eliciting expert opinion for economic models. Value in Health 10(3), 195–203.
- O’Hagan, A., et al. (2006). Uncertain judgements: Eliciting experts’ probabilities. Chichester: Wiley.
- Ouchi F. (2004) A literature review on the use of expert opinion in probabilistic risk analysis. World Bank Research Working Paper 3201. Available at: https://openknowledge.worldbank.org/handle/10986/15623.