Uncertainty In Economic Evaluation
Uncertainty exists wherever the truth is unknown either due to imperfect information or imperfect measurement. Within economic evaluation of healthcare, there are a number of sources of uncertainty. Methodological uncertainty relates to the analytic methods used to undertake an economic evaluation. Sources of methodological uncertainty include whether discounting should be employed and, if so, at what rate or rates, and whose preferences should be used to value health outcomes (those of the patient, public, or professional). Structural uncertainty relates to the structure and assumptions employed within an analysis. For example, the assumptions underlying the extrapolation of outcomes from a trial or the choice of the number of health states in a Markov model. This type of uncertainty is particularly relevant to (although not limited to) model-based analyses. It is often overlooked within analyses, largely due to the complexities of incorporating changes to structure and assumptions, despite the potential for considerable impact on results. Stochastic (or first order) uncertainty reflects differences in how interventions are experienced and impact within a population. For example, the different length and/or severity of adverse events experienced by different patients with the same prognosis receiving the same intervention. Stochastic uncertainty reflects random variation between people within the population and is represented by the sample variance (in trial-based studies) or the dispersion in the output from first order Monte Carlo simulation (in model-based studies). Uncertainty within the population is not the main focus for economic evaluation which is concerned, instead, with uncertainty at the population level. As such, stochastic uncertainty will not be covered in this article. Note that stochastic uncertainty is fundamentally different to heterogeneity which reflects the variation between people that can be explained by their specific identifiable characteristics. These characteristics might include, for example, age, gender, ethnicity, geographical location. Heterogeneity is best handled through the use of subgroups within the analysis, with results either presented independently for each subgroup or, if required, included in a weighted analysis for an aggregate group. Finally, parameter uncertainty reflects the uncertainty associated with specific parameters employed within an analysis. For example, the uncertainty surrounding the effectiveness of an intervention or the utility value associated with a particular health state.
Incorporating Uncertainty Within Economic Evaluation
The existence of these various uncertainties within an economic evaluation inevitably leads to uncertainty in the estimation of the costs, effects, and cost-effectiveness associated with the health intervention and ultimately to uncertainty in the decision about whether or not to fund the intervention. Undertaking an analysis of these uncertainties allows an assessment of the impact that they have on the results; illustrating the robustness of the results to changes in the inputs used in the analysis and assessing confidence in decisions. An analysis of uncertainty can also contribute to an assessment of the value of undertaking further research through a formal value of information analysis. According to the recent joint International Society for Pharmacoeconomics and Outcomes Research and Society for Medical Decision Making Modeling Good Research Practices Task Force Working Group Guidelines, ‘‘(t)he systematic examination and responsible reporting of uncertainty are hallmarks of good modeling practice. All analyses should include an assessment of uncertainty and its impact on the decision being addressed’’ (Briggs et al., 2012). This assessment of uncertainty usually takes the form of sensitivity analysis (SA), where assumptions or parameter values used in the economic evaluation are systematically varied to observe the impact on the results. Within deterministic SA (DSA), this systematic variation is performed manually to ascertain the impact associated with specific combinations of assumptions and/or parameters (see Section Deterministic Sensitivity Analysis). In contrast, probabilistic SA (PSA) involves repeatedly varying all of the uncertain parameters simultaneously, in order to get an overall assessment of the impact of the uncertainty. Of the sources of uncertainty described in Section Sources of Uncertainty, only parameter uncertainty can be assessed using either DSA or PSA. Methodological and structural uncertainties should not be assessed within a PSA. In addition, in certain circumstances scenario analyses are employed (e.g., when investigating heterogeneity). Here, alternative assumptions or parameter values associated with specific subgroups are substituted into the economic evaluation to examine the impact on the results.
Deterministic Sensitivity Analysis
DSA involves manually varying the parameter values or assumptions employed within the economic evaluation to test the sensitivity of the results to these values. There are a number of methods available to undertake DSA. One-way, two-way, and multiway SA involve substituting different values for one, two, or more parameter(s), method(s), or assumption(s) at a time and examining the impact on the results. The results of DSA can be displayed either graphically or through the use of tables, or conversely the results can be summarized in the text. This is fairly straightforward for one-way, two-way, and even three-way SA (which can employ contour plots) but becomes more of a challenge with multiway SA when more than three parameters are changed simultaneously. Analysis of extremes involves changing all parameters and/or assumptions to their most extreme values (which can be either best or worst case values) simultaneously and assessing the impact on the results. The results can be reported in the text. All these methods of DSA require that the range of values that the parameter(s) or assumption(s) can take is specified before the analysis. These ranges should be informed by and incorporate the available evidence base. In contrast, the final method of DSA, threshold analysis requires no such information. Here, the levels of one or more parameters, assumptions or methods are varied to identify the point at which there is a significant impact on the results, for example, the intervention becomes cheaper, more effective, or cost-effective. Again, the results can be displayed graphically, in tables or in the text. It is then left up to the user of the results to interpret and determine whether the values identified constitute reasonable levels for the parameter, assumptions, or methods.
Probabilistic Sensitivity Analysis
PSA involves repeatedly varying all of the uncertain parameters employed within an economic evaluation simultaneously, to get an overall assessment of the impact of the uncertainty. As such, PSA requires the specification of probability distributions for each parameter to fully reflect the parameter uncertainty. Each of these probability distributions represents both the range of values that the parameter can assume and the likelihood that the parameter takes any specific value within the range.
Assigning Probability Distributions To Parameters
Within a PSA there are three main methods for assigning probability distributions to parameters:
- Using patient-level data
- Using secondary data from the literature
- Assessing and incorporating expert opinion
Where sample data are available (e.g., from a clinical study) it can either be incorporated directly into the analysis through the use of bootstrapping (see Section Propagating uncertainty – bootstrapping) or the moments of the data can be used to fit a probability distribution.
Where historical data are available from previously published studies, this should be used to specify the probability distribution for the parameter. Here the premise is to match what is known about the parameter in terms of its logical constraints, behavior etc. with the characteristics of the distribution. As such, particular distributions are the most appropriate for specific parameters. For example, beta distributions should be used to specific uncertainty in probabilities, log-normal distributions should be used for relative risks or hazard ratios and gamma or log-normal distributions should be used for right-skewed parameters such as costs.
Where there are no primary or historical data available from which to specify the probability distribution for a particular parameter, then expert opinion can be used. However, care must be taken when eliciting opinions from experts, to ensure that it is the uncertainty in the parameter that is captured rather than various estimates of the mean. For example, the Delphi method is commonly used when eliciting expert opinion, however, this approach generally produces a single point estimate through consensus and therefore does not capture uncertainty. It is important that parameters are not excluded from the analysis of uncertainty because they have little information with which to estimate the parameter – these are precisely the parameters that need to be included, and with a wide distribution to represent the uncertainty.
Propagating Uncertainty – Monte Carlo Simulation
Once probability distributions are assigned to the parameters, the uncertainty is propagated through the use of (second order) Monte Carlo simulation. Here, a value is selected for each parameter from its probability distribution and the associated cost and effects are estimated based on these specific parameter values. These selections are most commonly made randomly from each probability distribution. Although recently, latin hypercube or orthogonal sampling (where selections are sampled from a specific section of the probability distribution) have been suggested to improve efficiency in sampling. The process is repeated thousands of times and a distribution of expected costs and effects is generated. These distributions reflect uncertainty at the population level, with each iteration representing a possible realization of the uncertainty that exists in the analysis, as characterized by the probability distributions.
Propagating Uncertainty – Bootstrapping
Within a trial-based study, an estimate of the population-level uncertainty can be obtained through bootstrapping the sample data. Here, samples are repeatedly taken at random from the original sample. These samples are each the same size as the original sample and are drawn with replacement. As with a (second order) Monte Carlo simulation, the bootstrap provides a distribution of the expected costs and effects associated with the intervention.
Presenting Uncertainty in Economic Evaluation
Tornado Plots
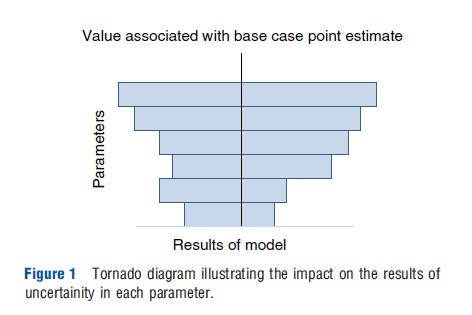
Tornado plots can be used to illustrate the impact on the results (i.e., costs, effects, or cost-effectiveness) associated with a series of one-way SA involving different parameters (Figure 1). Here, the uncertainty in the results associated with the uncertainty in each parameter is illustrated in a series of stacked bars (one per parameter). The length of each bar illustrates the extent of the uncertainty in the results associated with the uncertainty in that particular parameter. The parameters (bars) are stacked in order of length from smallest to longest (i.e., the parameters for which uncertainty in the parameter has the smallest impact on uncertainty in the results are at the bottom) forming a funnel or tornado shape. All of the bars are aligned around the result (cost, effect or cost-effectiveness) corresponding to the base case value for the parameter, hence the bars are not necessarily symmetrical and the funnel/ tornado is not necessarily smooth.
Cost-Effectiveness Planes
Uncertainty in the costs and effects associated with an intervention, generated either from a probabilistic SA or from bootstrapping trial data, can be graphically represented on a cost-effectiveness plane. Where the decision involves only two interventions, the incremental costs associated with the intervention of interest are plotted against the incremental effects for each iteration from the simulation, as a series of incremental cost-effect pairs, on an incremental cost-effectiveness plane. Incremental costs are conventionally plotted on the y-axis with incremental effects on the x-axis. As such, the slope between any specific cost-effect pair in the plane and the origin represents the incremental cost-effectiveness ratio (ICER) associated with that cost-effect pair (i.e., the incremental cost/incremental effect). The plane is split into four quadrants by the origin (which represents the comparator). The NE and SE quadrants involve positive incremental effects associated with the intervention of interest, whereas the NE and NW quadrants involve positive incremental cost. Figure 2 illustrates the joint distribution of incremental costs and effects as a cloud of points on the incremental cost-effectiveness plane.
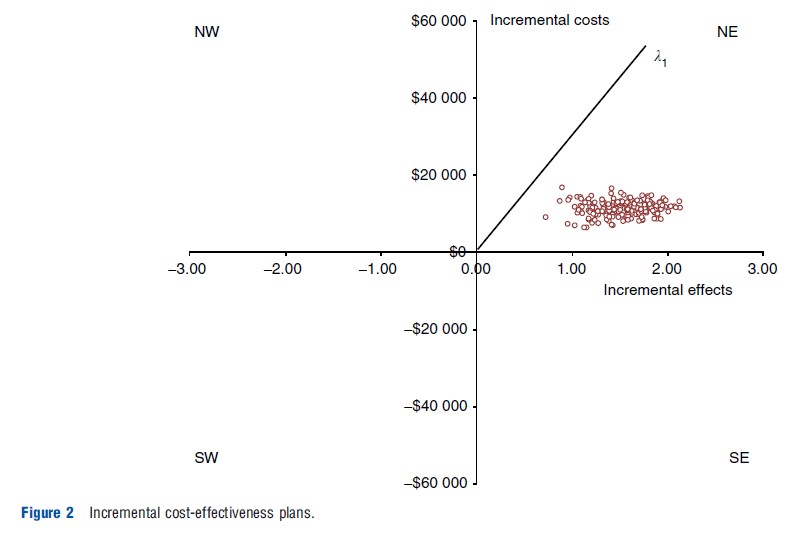
The location of the incremental cost-effect pairs in relation to the y-axis indicates whether there is uncertainty regarding the existence, or not, of cost-savings. For example, if all of the incremental cost-effect pairs are located above the origin (in the NE and/or NW quadrants) then the intervention is definitely more expensive. The spread of the incremental cost effect pairs in relation to the y-axis indicates the extent of the uncertainty regarding the magnitude of incremental costs. For example, in Figure 2, the incremental cost-effect pairs are plotted closely together in terms of incremental cost indicating that there is little uncertainty surrounding the magnitude of the incremental cost. The same holds for the location and spread of the incremental cost-effect pairs in relation to the x-axis and the existence and extent of uncertainty in the incremental effects. For example, in Figure 2, the location and spread of the incremental cost-effect pairs indicate that there is no uncertainty regarding the existence of an effect benefit associated with the intervention of interest (in comparison to the alternative) but that there is considerable uncertainty regarding the size of the effect benefit.
The incremental cost-effectiveness plane provides a good visual representation of the existence and extent of the uncertainty surrounding the incremental costs and effects individually. In addition, the location of the joint distribution of incremental costs and effects (the cloud of incremental cost effect pairs) within the four quadrants of the incremental cost-effectiveness plane can provide some information about the cost-effectiveness of the intervention. If the cloud is located completely in the SE quadrant (or the NW quadrant) then there is no uncertainty in the cost-effectiveness; the intervention dominates (is dominated by) the alternative. Where the cloud of incremental cost-effect pairs falls into the NE or SW quadrants or straddles more than one quadrant, the incremental cost-effectiveness plane does not provide a useful summary or assessment of the uncertainty in the cost-effectiveness. In addition, a distinction must be made between uncertainty in the cost-effectiveness of the intervention and uncertainty in the decision to adopt the intervention based on the current information about costs, effects and cost-effectiveness (decision uncertainty). Decision makers using the results of economic evaluations to guide decisions about whether to adopt new interventions are interested in the latter. An assessment of the decision uncertainty requires the comparison of the joint distribution of the incremental costs and effects with a predetermined, external threshold level representing the willingness to pay for the effects (λ) to determine the proportion of the joint distribution that falls below the threshold. The assessment of the decision uncertainty is not too daunting when the cloud of incremental cost and effect pairs falls into just one or even two quadrants, or when the cost-effectiveness threshold is known with certainty. Returning to Figure 2, at a willingness to pay threshold of λ1 there is no uncertainty associated with the adoption of the intervention despite the considerable uncertainty in the cost-effectiveness of the intervention. This is because the entire joint distribution of incremental costs and effects falls below (to the South and East of) the cost-effectiveness threshold (λ1). Where the cloud of incremental cost-effect pairs falls into the SE or NW quadrants there is also no decision uncertainty; the intervention is definitely cost-effective (SE) or definitely not cost-effective (NW). When the joint distribution of costs and effects covers three or all of the quadrants, or the cost-effectiveness threshold is unknown then the assessment of the decision uncertainty will involve considerable computation, and the incremental cost-effectiveness plane will not provide a useful summary of the decision uncertainty.
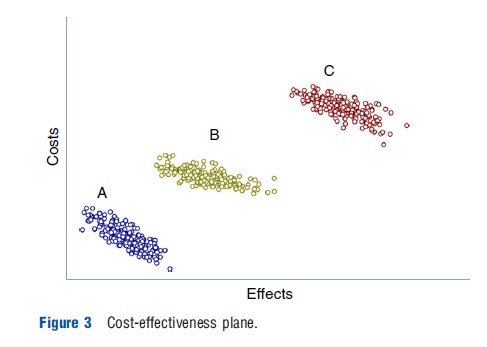
Where the decision involves more than two interventions, the costs and effects for each intervention are plotted (for each iteration from the simulation) as a series of cost-effect pairs, on a cost-effectiveness plane (see Figure 3). Here, the spread of the cost-effect pairs for an intervention in the y-axis (x-axis) provides information on the extent of the uncertainty in the costs (effects). In addition, the location of the cost-effect pairs for an intervention in comparison to the cost-effect pairs for other interventions provides some information about the existence of uncertainty in the incremental costs and incremental effects. For example, in Figure 3, it is possible to determine that intervention B is definitely more expensive than intervention A (incremental cost is positive), but it is not possible to determine that it is more effective than intervention A. In contrast, intervention C is both more costly and more effective than both A and B. For decisions involving more than two interventions, the cost-effectiveness plane can not provide an assessment of the uncertainty in the cost-effectiveness or an assessment of the decision uncertainty. For these assessments, knowledge is required regarding the relationship between each of the cost-effect pairs for each intervention (i.e., which cost-effect pair for intervention A relates to which cost-effect pair for intervention B and which cost-effect pair for intervention C). This information is not easily presented or computed in the cost-effectiveness plane.
Cost-Effectiveness Acceptability Curves
Cost-effectiveness acceptability curves (CEAC) provide a graphical representation of the decision uncertainty associated with an intervention. They present the probability that the decision to adopt an intervention is correct (i.e., that the intervention is cost-effective compared with the alternatives given the current evidence) for a range of values of the cost-effectiveness threshold (λ). This probability is essentially a Bayesian definition of probability (i.e., the probability that the hypothesis is true given the data), although some commentators have given the CEAC a Frequentist interpretation.
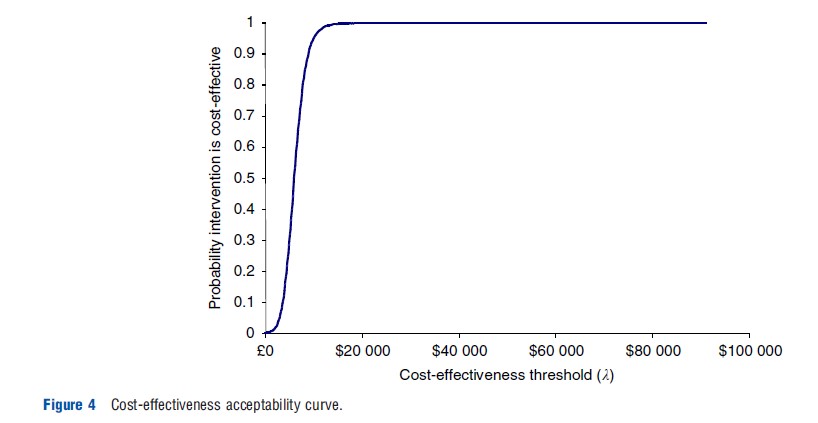
Where the decision involves only two interventions, the decision uncertainty is derived from the joint distribution of incremental costs and effects, as the proportion of the incremental cost-effect pairs that are cost-effective. In an incremental cost-effectiveness plane, this can be identified as the proportion of cost-effect pairs that fall below a specific cost-effectiveness threshold (as described above). The CEAC is then constructed by quantifying and plotting the decision uncertainty for a range of values of the cost-effectiveness threshold (λ). As noted in Section Cost-Effectiveness Planes, incremental cost-effect pairs that fall in the SE (or NW) quadrant are always (never) cost-effective, as such these incremental cost-effect pairs are always (never) counted in the numerator of the proportion. Incremental cost-effect pairs that fall in the NE and SW quadrants are either considered cost-effective or not depending on the cost-effectiveness threshold (λ). When the cost-effectiveness threshold (λ) is zero (i.e., the decision maker places no value on effects), only incremental cost-effect pairs in the SE and SW quadrants will be considered cost-effective (i.e., those with negative incremental costs). When the cost-effectiveness threshold (λ) is infinite (i.e., the decision maker only values effects and places no value on costs), only incremental cost-effect pairs in the NE and SE quadrants will be considered cost-effective (i.e., those with positive incremental effects). Between these two levels, as the cost-effectiveness threshold (λ) increases (i.e., the decision maker increasingly values effects), incremental cost-effect pairs in the NE (SW) quadrant are added to (removed from) the numerator. This reflects the fact that incremental cost-effect pairs in the NE quadrant (i.e., positive cost, positive effect) increasingly provide effects at a cost lower than the decision maker would be prepared to pay, whereas those in the SW quadrant involve a loss of effects without the level of savings that the decision maker would require. As a result, the CEAC does not represent a cumulative distribution function; its shape and location will depend solely on the location of the incremental cost-effect pairs within the incremental cost-effectiveness plane. Figure 4, presents a CEAC for a decision involving two interventions. By convention, for decisions involving only two interventions, the CEAC is only shown for the new intervention of interest, however, the CEAC for the alternative could also be presented. Given that the interventions are mutually exclusive and collectively exhaustive (i.e., for each incremental cost-effect pair the new intervention is either cost-effective or the alternative is cost-effective) then the CEAC for the alternative has the opposite shape and location, with the curves crossing at a probability of .5.
Where the decision involves more than two interventions, CEACs can be constructed for each intervention by determining the decision uncertainty associated with each intervention compared to all of the alternatives simultaneously (i.e., the probability that the intervention is cost-effective compared with all of the alternatives given the current evidence). Again, as the interventions are mutually exclusive and collectively exhaustive (i.e., for each cost-effect pair intervention only one of the interventions A, B, or C is cost-effective) then the CEAC for every intervention will vertically sum to one. It is inappropriate to present a series of CEACs that compare each intervention in turn to a common comparator, as this provides no indication of the uncertainty surrounding the decision between the interventions. Figure 5 presents a series of CEACs associated with a decision involving more than two interventions.
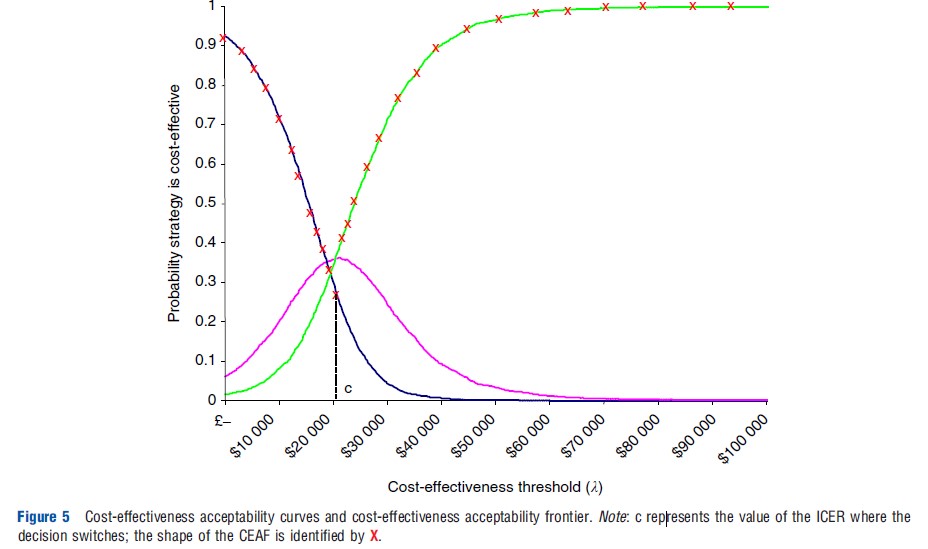
It is very important to stress that the CEAC simply indicates the decision uncertainty associated with an intervention for a range of values of l. Thus, in the context of expected value decision making (where the decision is made on the basis of the expected costs, effects, and cost-effectiveness) the CEAC does not provide any information to aid the decision about whether to adopt the intervention or not. Therefore statements concerning the CEAC should be restricted to statements regarding the uncertainty surrounding the decision to select a particular intervention, or the uncertainty that the intervention is cost-effective, compared with the alternatives given the current evidence. Information from the CEAC should not be used to make statements about whether or not to adopt an intervention.
The cost-effectiveness acceptability frontier (CEAF) has been suggested to supplement the CEAC in the context of expected value decision making. The CEAF provides a graphical representation of the decision uncertainty associated with the intervention that would be chosen on the basis of expected value decision making. As such, the CEAF provides no additional information about the decision uncertainty, it simply replicates the CEAC for the intervention that would be selected by the decision maker at each value of the cost-effectiveness threshold (λ). As such, discontinuities occur in the CEAF at values of the cost-effectiveness threshold (λ) at which the decision alters (see Figure 5).
Intervals And Distributions For Net Benefits
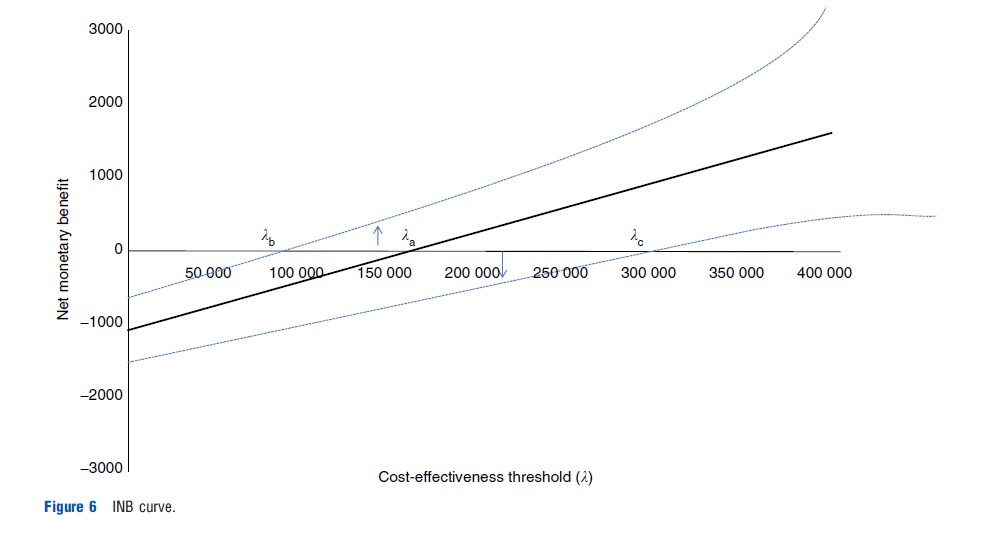
Net benefits (NB) have been suggested as an alternative method to present the results of economic evaluations. In this framework, the issues associated with ICERs are overcome by incorporating the cost-effectiveness threshold (λ) within the calculation to provide a measure of either the net health benefit or the net monetary benefit. Here, following a probabilistic SA or bootstrap of trial data, the cost and effect pairs for every iteration are replaced by an estimate of NB; generating a distribution of net benefit. Where the decision involves two alternatives, the incremental net benefit (INB) can be used. The uncertainty can be either be summarized and presented as a confidence interval for (I)NB or presented in full as a distribution of (I)NB. Given that the net benefit measure incorporates the cost-effectiveness threshold, where the threshold is unknown the results must be provided for a range of values of the threshold. Figure 6 presents the confidence interval for the INB for a range of values of the cost-effectiveness threshold as an INB curve. This curve provides information about the extent of the uncertainty in INB as well as identifying which intervention to adopt (on the basis of expected value decision making) for every value of the cost-effectiveness threshold (λ). For example, in Figure 6 for values of the threshold above λa the intervention should be adopted (as the INB>0), below la the alternative should be adopted. With regard to the decision uncertainty associated with the intervention, at values for the threshold below λb there is no decision uncertainty; the intervention is not cost-effective. At values for the threshold above λc there is no decision uncertainty; the intervention is cost-effective. For values of the threshold between λb and λc assessment of the decision uncertainty associated with the intervention requires an evaluation of the proportion of the distribution of INB that falls above zero (i.e., the vertical distance from the x-axis to the 95% line). The decision uncertainty associated with the comparator is given by the proportion of the distribution of INB that falls below zero (i.e the vertical distance from the 5% line to the x-axis). Figure 7 presents distributions of NB for a particular value of the cost-effectiveness threshold (λ). As noted earlier, where the threshold is unknown the distributions would have to be provided for a range of values of the threshold. Figure 7 provides information about the extent of the uncertainty in the NB associated with each intervention as well as identifying which intervention to adopt (on the basis of expected value decision making) for a specific value of the cost-effectiveness threshold (l). An assessment of the decision uncertainty associated with an intervention would require an evaluation of the proportion of the distribution of NB that overlaps with the NB distributions associated with the other interventions. Where the decision involves more than two interventions, this evaluation is not straightforward. Therefore it is only in the situation that the NB distributions are distinct (i.e., do not overlap) and there is no decision uncertainty, that the figure provides any information about the decision uncertainty associated with the interventions.

Linking Analysis Of Uncertainty To Decision Making
The presence of decision uncertainty means that there is inevitably some possibility that decisions made on the basis of the available (uncertain) information will be incorrect and introduces the possibility of error into decision making. Where the decision maker has the authority to delay or review decisions (based on either additional evidence that becomes available, or that they request) an analysis of uncertainty is important because it links to the value of additional research.
References:
- Briggs, A. H., Weinstein, M. C., Fenwick, E. A. L., et al. (2012). Model parameter estimation and uncertainty analysis. A report of the ISPOR-SMDM modeling good research practices task force working group. Medical Decision Making 32, 722–732.
- Briggs, A. H. (2001). Handling uncertainty in economics evaluation and presenting the results. In Drummond, M. F. and McGuire, A. (eds.) Economic evaluation in health care: Merging theory and practice, ch. 8, pp. 172–215. Oxford, UK: Oxford University Press.
- Briggs, A. H. and Gray, A. M. (1999). Handling uncertainty when performing economic evaluation of healthcare interventions. Health Technology Assessment 3(2), 1–63.
- Briggs, A. H., Sculpher, M. J. and Claxton, K. P. (2006). Decision modelling for health economic evaluation. Handbooks in health economic evaluation. Oxford, UK: Oxford University Press.
- Briggs, A. H., Weinstein, M. C., Fenwick, E. A. L., et al. (2012). Model parameter estimation and uncertainty analysis. A report of the ISPOR-SMDM modeling good research practices task force working group. Value in Health 15, 835–842.
- Claxton, K. (2008). Exploring uncertainty in cost-effectiveness analysis. Pharmacoeconomics 9, 781–798.
- Fenwick, E., Claxton, K. and Sculpher, M. (2001). Representing uncertainty: The role of cost-effectiveness acceptability curves. Health Economics 10, 779–787.
- Fenwick, E., O’Brien, B. and Briggs, A. H. (2004). Cost-effectiveness acceptability curves: Facts, fallacies and frequently asked questions. Health Economics 13, 405–415.
- Hunink, M., Glasziou, P., Siegel, J., et al. (2001). Decision making in health and medicine. Integrating evidence and values. In Hunink, M., Glasziou, P., Siegel, J., et al. (eds.) Variability and uncertainty, ch. 11, pp. 339–363. Cambridge, UK: Cambridge University Press.