Introduction
Publicly funded health care systems require some form of resource allocation funding principles, usually in the form of formulae, to enable the payer (typically a government body) to distribute health care budgets across population groups. Population groups are typically defined by geography and a population within each geographic boundary is likely to have variations across individuals within it both in terms of health and in the utilization of healthcare services.
To distribute health care budgets efficiently requires knowledge of how population groups differ, which in turn relies on up-to-date data on population variations in the need for health care. Need, taken here as the capacity to benefit, is difficult to measure. Poor data availability usually results in need being proxied by service utilization, with the assumption that populations with higher needs will have higher rates of health care services use. Precision is therefore not really to be expected in matching budgets to local needs, because data on neither can be perfect. Perhaps the best that can be expected is that formulaic solutions push the system in the right directions.
Utilization, however, reflects access to care which may be the product of both demand (influenced by an individual’s need for care, how affordable care is to the individual and whether the individual is willing to accept care) and supply factors (whether the individual has providers of care in their area and whether care is available). If access varies by geographic population groups, funding formulae using utilization measures alone to allocate budgets could reinforce inequalities and inefficiencies in both health and access to health care.
An alternative way of measuring need is to use demographic and/or health related population characteristics as a proxy (e.g., a mortality ratio, which assumes populations with higher needs have higher mortality ratios). Although such proxies can serve as an alternative to measuring need as utilization, they are most frequently seen as complementary measures, the assumption being that they detect different aspects of need.
Weighted capitation methods are typically used to apply a needs-based approach to resource allocation in health care. These methods weight populations by indices of need and are used to determine each population group’s share of the health care budget.
The main challenge in designing resource allocation formulae is that they ought to allocate health care budgets in accordance with the payer’s objectives. The payer’s objectives typically relate to efficiency, equity, or more likely, a mixture of both. The prime concern lies with whether the funding formulae used to derive allocations is efficient, i.e., pushes the system toward maximizing the health of society given the resources available, or whether there is potential for inefficiencies in the funding formulae such that the push is in the wrong direction. This article investigates how weighted capitation approaches, and the payer’s efficiency-equity objective, impact on the efficiency of the resource allocation funding formulae used to distribute health care budgets.
The article is structured as follows. First, what is meant by efficiency in the resource allocation formulae is explained and examples provided of the conflict between efficiency and equity in resource allocation using two population groups. Second, the extent to which the formulae impact or are impacted by technical efficiency is looked at. Examples of how the resource allocation formulae have developed since the introduction of the National Health Service (NHS) in England, and the impacts of these changes on efficiency are then given. Much of the discussion presented on the efficiency of using a weighted capitation approach in England is applicable to other international settings. While the methods for the financing of health care in the developed world vary widely, there has been increasing use of capitation payments. The final section provides the article summary.
Efficiency
A Production Possibility Frontier Approach To Resource Allocation
Economic efficiency consists of two types of efficiency, allocative and technical efficiency. Allocative efficiency concerns producing the maximum output subject to inputs, i.e., it is not possible to increase output simply by reallocating resources, and it is achieved by equalizing the marginal capacity to benefit from additional funds across all inputs, while technical efficiency concerns utilizing a specified combination of inputs to produce maximum output. From a resource allocation perspective economic efficiency concerns maximizing the value of output (health gains and/or prevention) from given resources.
The problem with measuring efficiency in health care is that it is not obvious how to define the output of interest: is it health care use? Access to health care? Or measures of health gains or outcomes? Further, how can such data be obtained? Hollingsworth (2008) provides a review of the literature surrounding the measurement of production frontier efficiency in health care. The answers to these questions are not obvious, and will likely invoke some normative judgment.
Figure 1 gives a graphical representation of a production possibility frontier (PPF) for a public service, that is, the plot of health outcomes associated with spending on a population group (this example, and what follows is adapted from Smith (2007)). The aim is to determine the optimum payment for the population group given the payer’s efficiency and equity objectives. The PPF relates expenditure (X) on the population group to the health outcomes (Y), and is a cumulative outcome for all individuals within the population group. The more productive the population group is in generating health, the higher the PPF lies. In this simple example it is assumed that no historic spend feeds into present health, and that population groups with zero public health care expenditure may have a positive health outcome. This may be because of private utilization of health care services, for example. This figure, and all subsequent figures are illustrative, and not much should be read into the intercept.
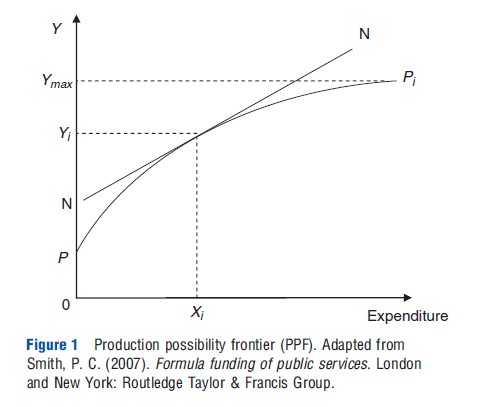
The PPF for population group i (PPi in Figure 1) represents outcomes for payments where technical efficiency holds (efficient production of the health care by the providers serving the population group). Further assumptions are that there are decreasing returns to expenditure (the PPF is concave), that there is only one input (or alternatively that all inputs can be aggregated to one measure, in this example, budget allocations) and one output (some measure of health such as life-years gained, whose value is independent of the identity of those in whom it is embodied), and that other factors such as different providers, complimentary services, the environment, personal characteristics, and societal influences are exogenous to the shape of the PPF. The time period is assumed to be 1 year (that, in reality, is typically the time frame used for allocated budgets).
The need of population i can be measured as the difference between the level of health at a particular level of expenditure, and the maximum health attainable. In the case with unlimited funds, one may expect to observe expenditure up to the point where the benefit (additional health) of additional expenditure is zero (i.e., where further need is zero). This is where the PPF flattens out (Ymax). Unfortunately, resources are scarce, and the available budget allocated to health care (which in itself is also an issue for efficiency at the State level) may not be enough to ensure that maximum health is attained. With an allocated health care budget payers have to determine how to distribute this across geographic populations.
Figure 1 highlights, in this simple example, how determining the amount of expenditure determines the outcome achieved. With this in mind, and with knowledge of each geographic population’s PPFs, the payer can optimize a social welfare function.
The payer determines the social welfare function and hence marginal social value (slope of NN in Figure 1), essentially a cut-off cost above which no more treatment is offered. The payer provides expenditure up until the point where additional expenditure results in less health produced than is valued by society. Only at expenditure Xi does the marginal social value of the payer meet the marginal gain in health outcome (benefit). Expenditure less than Xi corresponds to a higher marginal benefit than marginal social value (the slope of the PPF is steeper than the slope of the welfare function, NN). Expenditure greater than Xi corresponds to a lower marginal benefit than marginal social value (the slope of the welfare function, NN, is steeper than the slope of the PPF). A steeper social welfare function would have a higher marginal social value of expenditure, and this would imply optimum expenditure at a higher marginal gain in health, which would lie to the left of Xi. To be allocatively efficient the payer should equate the marginal social value to the marginal benefit, this would be at expenditure Xi and corresponds to the pure efficient solution to resource allocation. The pure efficient solution maximizes aggregate outcomes, and is where expenditures are allocative and technically efficient. Alternative allocations would result in a reduction in total health produced.
The Divergence From Pure Efficiency
In reality there are two main reasons why the pure efficiency solution above is never met. First, allocations may not be set at the point where the marginal capacity to benefit from expenditure equals the marginal social value. This may be because of inaccurate needs measurement, differences in the cost of delivering health care across population groups, or as a result of an alternative equity objective held by the payer. Second, although the payer may distribute budgets efficiently, budgets might not be spent efficiently by providers serving the geographic populations (technical inefficiency). This section will look at each case.
Inaccurate Needs Measurement
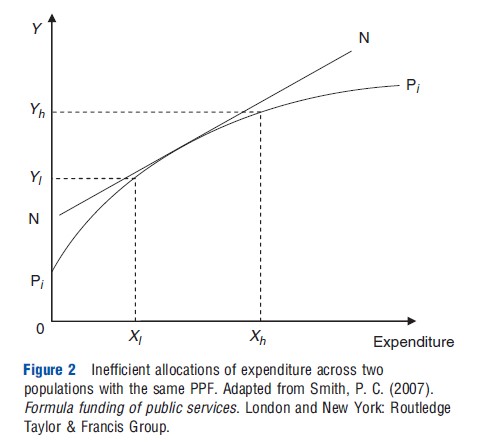
Where expenditures do not reflect need, the implication is that populations of equal (risk adjusted) marginal need receive different budgets. Figure 2 gives a graphical example. In this case, two populations have equal need and are equally productive (the PPFs for the two populations are the same and overlap), but receive different allocations, Xl and Xh. One population receives Xl and resulting outcome Yl, while the other receives Xh and outcome Yh. Allocative efficiency does not hold here since redistributing funds so each population group receives the same expenditure would increase outcomes in total. This is because the increase in expenditure to the low-resource population (l) results in greater gains in outcome than the loss in outcome from decreasing expenditure to the high-resource population group (h). The four main ways in which inaccuracies arise are described below.
Utilization Methods To Model Need
Utilization data is largely employed in resource allocation formulae to help model the needs of different geographical populations. This assumes that higher utilization of services reflects a higher capacity to benefit from expenditure. There are a variety of methods available to weight geographic populations based on utilization data. For example, one can weight populations based on the share of total utilization, or apply average utilization rates to the age and/or gender breakdown of geographic populations. Detailed econometric methods can also be applied, enabling a multitude of population characteristics to explain variations in utilization across population groups. This approach regresses geographic population level utilization on variables thought to identify needs. The estimates from the regression are then used to weight the geographic population’s share of the budget to reflect the differences in need across each geographic population.
Analyzing utilization data to direct budget allocations poses two potential problems, the first being that only observed (met) needs are modeled. Under (and over-) utilization by population groups will be sustained in this setting. The second concerns the effect of supply-side impacts on utilization. Variations in utilization may be because of differences in provider provision of services rather than need.
Unmet Need
Unobserved (unmet) need can either be general or specific. General unmet need is nondiscriminatory across all geographic population groups, such as a lack of health care services for all. This does not bias the formulae since the unmet need represents a common proportionate lack of health care meaning relative needs weights to population groups remain valid. Specific unmet need is discriminatory, affecting certain geographic population groups because of their population makeup. For example, if utilization is lower for minority ethnic groups, population groups with higher rates of minority ethnic groups would receive a lower weighting than would be if the needs of minority ethnic groups had been observed. To control for specific unmet need, estimates with the ‘wrong’ sign in regressions explaining utilization may be held back from being part of the funding formulae weights (for example, negative estimates for minority ethnic groups where no clinical explanation for an ethnic difference is identified).
Illegitimate Supply
Illegitimate supply-side factors are where variations in utilization reflect providers’ provision of services rather than the needs of population groups. For example, utilization approaches could reinforce any existing inefficiency in maintaining service provision levels that may in part reflect an access to health care issue (such as differences in waiting times for hospital surgery or in the availability of General Practitioners across geographic population groups). Methods to control for any illegitimate supply-side factors include the addition of geographic population group dummies in a regression to control for group average variations that are over and above the observed variations across geographic population groups.
Age And Gender Weighting
Age and/or gender weights may be applied to the resource allocation formulae, in addition to, or in place of, utilization modeling. The motive for such an inclusion is the notion that health needs vary over the life cycle and by gender. To be accurate these must fully explain variations in need. This, however, is unlikely, given numerous other factors including socioeconomic status, education, and sociodemographic characteristics have been found to explain variations over and above age and gender.
Incorporating Concerns For Health Inequalities
Geographic populations may differ, in part, because of demographical or epidemiological factors. Differences in geographic populations may mean that the same level of expenditure will result in different health outcomes between geographies. That is, differences in productivity result in different PPFs across geographic populations. How productive a population group is determines the height and/or slope of the PPF. Differences in the height of PPFs across population groups do not alter the allocations made under pure efficiency. However, differences in the slope of the PPF across geographic populations have important implications for the pure efficient allocation. For the payer to maximize outcomes, it has to adjust expenditure and outcomes by marginal need. Needs adjustment will make the marginal social benefit from expenditure equivalent across geographic populations, meaning the same sloped line is applied to all geographic populations, irrespective of their PPF. Applying the same sloped line means across each geographic population the marginal social value and marginal benefit are equal at the allocative efficient levels of expenditure. At these levels an additional increase in expenditure results in the same increase in benefit (health) for each geographic population. This can be seen as the pure efficiency solution. Any variation from this leads to a net reduction in the sum of outcomes.
Assuming needs have been fully captured in the resource allocation formulae, the pure efficient solution is consistent with different geographical populations attaining different levels of health. For example, one population may be less productive, with a lower PPF, shown by P1 in Figure 3. With no funding formulae, the payer may divide the budget into two, say X*. At X* the capacity to benefit from expenditure is greater for the less productive population. Utilization rates may reveal that the less productive population has higher utilization because of the population being relatively older than the more productive population. Weighting X* on the basis of differences in utilization by age may direct allocations to X1 and X2. Under the pure efficiency outcome (where N1 and N2 have the same gradient), although the less productive population group receives a higher budget allocation than the more productive population, X1>X2, there are differences in health outcomes across the two populations, Y2>Y1.
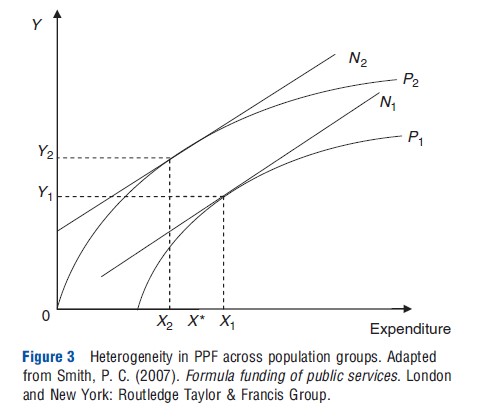
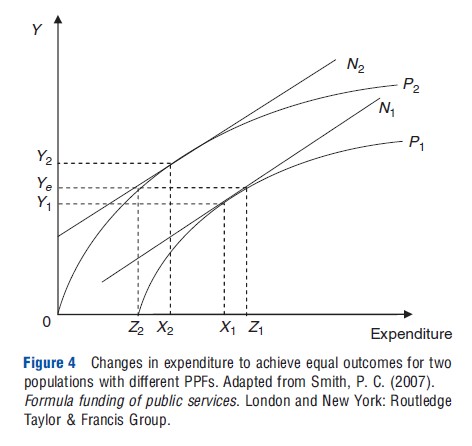
However, differences in health outcomes across population groups may not be seen as equitable. Policy aims have an important impact on how this inequality should be targeted. Figure 4 gives the expenditure required to ensure both population groups in the example attain the same health, Ye. The pure efficient solution has differing health outcomes and payments, so to attain Ye requires increasing allocations to the less productive population (Z1>X1), and decreasing allocations for the more productive population (Z2<X2). As both population allocations are now allocatively inefficient (but still technically efficient), the allocation is less efficient (Y1+Y2>2Ye).
Equity Versus Efficiency
Figure 4 highlights the trade-off in health outcomes when equity or efficiency are maximized. An alternative way to present the trade-off is given in Figure 5. The North-West and South-East quadrants give the PPF for the high productive and low productive populations respectively; the North-East quadrant maps the two production frontiers together to attain total output possibilities between the two populations. The South-West quadrant gives the budget line, with all points on the line sum to the total budget available. Weighted capitation would provide the weight applied to each population. The total outcomes for the two populations are obtained by: allocating expenditure between the two in the south-west quadrant, mapping these to the PPFs for each population in the North-West and South-East quadrants, and finally mapping these to the production possibility frontier in the NorthEast quadrant. The line N in the North-East quadrant gives the relative marginal social value of each population’s outcome. Here it is assumed to be symmetric. The payer’s welfare function (and hence slope of N) will dictate how allocatively efficient the allocation is (note it is still assumed technical efficiency holds). The allocations under the pure efficiency solution, where total outcomes are maximized and the marginal capacity to benefit from additional expenditure is equivalent across population groups (W* in the North-East quadrant), would be point BW. The alternative equal outcomes objective, where equal outcomes are attained between the two groups (E* in the North-East quadrant), would be under al-locations at BE. Total outcomes will be inefficient (lower) under the equal outcomes solution (E*) than the efficient solution (W*).
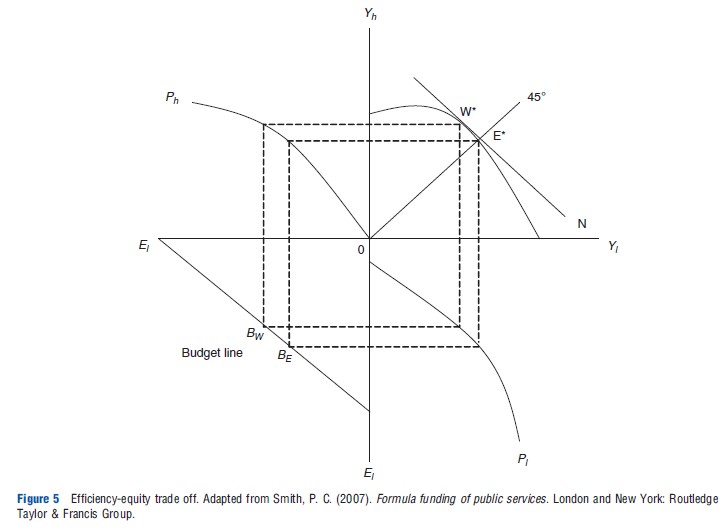
Avoidable Inequalities In Health
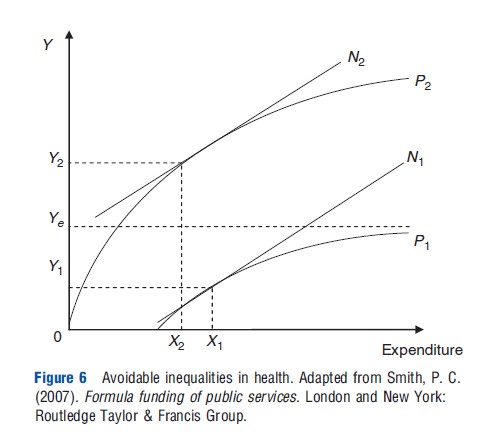
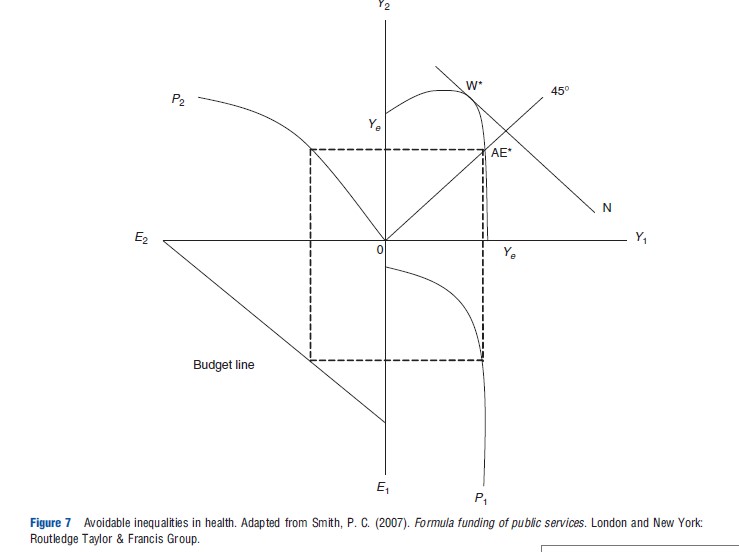
One implication of populations having different PPFs is that some populations may never be able to attain a state of health that equals the average across the total population. Figure 6 gives an example where the maximum possible health achievable is lower for one population than the average of the two (Ye is above the PPF for the less productive group at all points). Figure 7 gives the four quadrant representation. In this example, any attempt to achieve equal outcomes in health will fail (no amount of allocation could ensure the less productive population will reach Ye). The best the payer can hope to achieve is to ensure the removal of avoidable inequalities in health outcomes. In terms of Figure 7, this means allocating at the point where the PPF for the less productive population begins to flatten (the maximum that population group can achieve). Note how, compared to the pure efficiency solution (W*), the equal health outcome (AE*) requires a relatively greater loss in potential health for the more productive population than the negligible gain in health for the less productive population.
Differing Costs In The Delivery Of Health Care
The costs of delivering health care may vary across geographic population groups, and not controlling for this will inflate (deflate) allocations for low (high) cost population groups. Effectively, differing costs mean allocated budgets are worth more (or less) in different geographic populations. This may be seen as a reduction (increase) in the budget allocations for high (low) cost geographic population group, making allocations no longer efficient. This is particularly problematic if there exists a correlation between costs and productivity. For example, if less productive population groups face higher cost then allocations will not be at the level sufficient to reflect the expenditure required to deliver the health care for the respective need.
Measuring Allocative Inefficiency
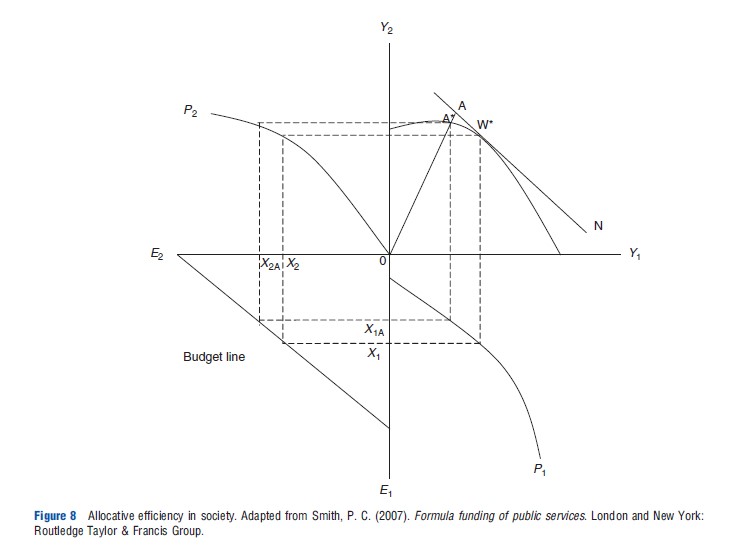
The issue concerning the resource allocation formulae is one of determining how to distribute the budget across population groups. Figure 8 gives the four quadrant representation of Figure 3, where it is assumed that the payer’s objective is the pure efficient outcome with the resulting maximization of output, W*. Assume however, that the weighted capitation formulae have failed to identify needs of the population groups accurately. The result is higher payments to the more productive population (X2A>X2) and lower payments to the less productive population (X1A<X1) than would have been if needs were correctly identified. The resulting outcome is at A *, where the level of allocative inefficiency is 0A */0A. The failure to identify needs correctly results in a lower output of health A*<W*.
Assuming the more productive population has lower costs in the delivery of health care, the effect of differences in the cost of delivering health care across population groups could also be seen in Figure 8. Here the differences in costs inflate the budget allocated to the high productive population (X2A>X2), and deflate the budget allocated to the low productive population.
Technical Inefficiency
Until now it has been assumed that the budgets allocated to population groups are spent efficiently, utilizing the budget to attain the maximum health possible. There is, however, an ever growing number of studies that investigate the efficiency of providers. Hollingsworth et al. (1999) provided a review of methods used to model technical efficiency. The potential for technical inefficiency arises because of factors within the formulae, within the structure of the health care system, and external to health care.
Within The Formula: Budget Risk
A key issue arising with budgeting health care funds is that of budget risk. Because of uncertainty in the demand for health care, variations in practice across providers, and potential errors in the capitation formulae, health care expenditure is unlikely to match budgets allocated. This may lead to resources being used on the basis of budget availability rather than need. Budget risks are likely to increase the smaller the geographical area used, the shorter the time horizon, and for more limited types of care.
There may be the possibility that the resource allocation formulae present incentives to be technically inefficient. For example, if budgets are directed toward high need populations, this may present an incentive to undertreat populations to sustain high(er) budgets.
Further complications with the budgets arise since any budget underspend is not redistributed. There is an incentive for underbudget providers to behave inefficiently, that is, spend over and above what they (efficiently) need to provide health care to use up the budget.
Since most resource allocation formulae incorporate past usage (as used in utilization models) any inefficiencies in provision is reinforced. The needs weights will be generated from utilization that is potentially inefficient and inequitable. If past allocations were inefficient future allocations based on these prior allocations will also be inefficient. To ensure inefficiencies are not sustained, the causes of the inefficiencies should be targeted, for example, access to services. A potential way forward would be to incorporate measures of withinprovider efficiency and equity into the formulae. For example, budget allocations may include a weight for relative efficiency (however this is measured) or for relative equity in health (however defined), which could penalize providers who do not channel budgets to target inefficiency and poor access.
Within The Health Care System: Market Failure
The market structure of the health care system could lead to inefficiencies. For example, in England the NHS is essentially a monopolistic employer and provider of health care resources. The NHS is not subject to competitive market forces that may provide pressure to ensure the NHS system works efficiently, at lowest cost with most impact. For example, the frequency of restructuring the administration of the NHS highlights the struggle to streamline NHS administration and ‘red tape’ present in the system: allocations were originally made to 14 geographic population groups, but this figure has grown over the years: for 1996–97, to 100; for 2003–04, to 303; and since 2006, to 152 geographic population groups.
External Factors
There are also economic influences that may affect the overall delivery of health care. The recent recession, for example, has led to pressure on publicly funded health care systems’ budgets, which have been cut in real terms. The effects of this could, for example, lead to the encouragement of better (more) efficient procedures and structures both between and within the sectors and services of the health care system.
Impact On Efficiency
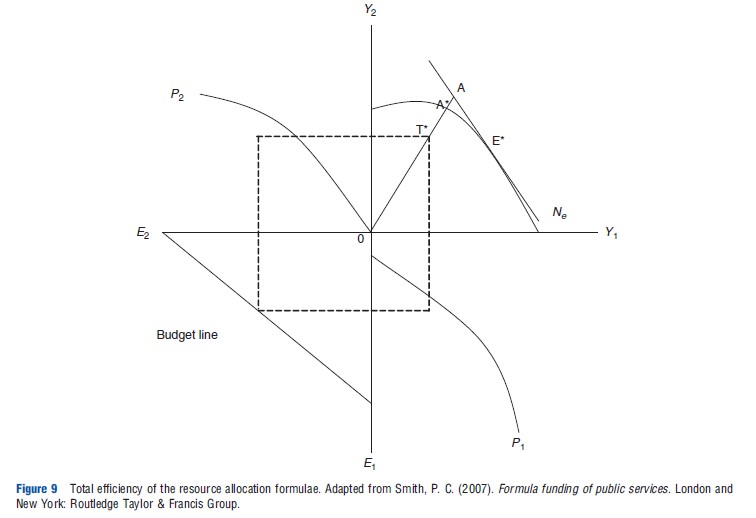
In terms of the example, Figure 9 shows the implications of technical inefficiency. Now the outcome (T*) in the North-East quadrant is not on the PPF of both population groups. Relaxing the assumption of technical efficiency would mean allocations do not produce the maximum health for populations. One moves south and/or westwards in the north east quadrant reflecting reductions in output because of technical inefficiency.
The Current NHS Resource Allocation Formulae In England
In England the amount of public funds allocated to health care from taxation is politically determined. The Treasury sets aside a total spend on the NHS health care in the annual Budget. Of this, the Department of Health (DH) then assigns the total budget for the three largest ‘programmes’ of NHS service. These are Hospital and Community Health Services (79% of the budget), Prescribing (11%), and Primary Medical Services (10%). Within these budgets, weighted capitation methods are applied to generate a target share of the budget for each Primary Care Trust (PCT), of which there are currently 152 across England. PCTs receive a lump sum to spend across the three programmes as they deem fit.
The DH has used variations of weighted (risk adjusted) capitation payments for distributing budgets for NHS health care across England since 1977–78. The aim of the current formulae used to determine the capitations is to enable PCTs ‘‘to commission similar levels of health services for populations with similar need, with the further objective, since 1999, of helping to reduce avoidable health inequalities’’ (Department of Health, 2011, p.7).
The services provided by the NHS are not free to the user, because, while free at the point of consumption, individuals pay indirectly via taxation. The taxes used to fund the NHS health care services are substantive: the current weighted capitation approach is used to allocate some $132 billion to PCTs for the 2011–12 financial year, and the NHS as a whole accounted for over 8% of UK Gross Domestic Product for 2010–11.
The weighted capitation formula generates target allocations based on PCT populations, adjusted for: the age distribution; additional need over and above observed age structure; and differences in costs of delivering the services across PCTs – the Market Forces Factor (MFF). A separate index is given to each of these three components, and these are multiplied together to give a weighted population for each PCT in each program (see eqn [1]).
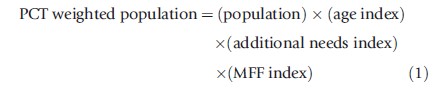
These weighted populations are then combined according to the share of each program to the total budget. The weighted population for each PCT is then multiplied by the total budget to give a target allocation. PCT allocations, however, are not solely determined by weighted capitation methods. Actual allocations are obtained by taking the difference between target allocations and the previous year’s allocation (adjusted for any transfers in responsibilities). A ‘pace of change’ policy then sets the differential growth in allocations that PCTs receive in addition to the previous year’s allocation. The growth component is determined by national and local priorities, and the distance between last year’s allocations from target allocations.
Different weighted capitation models are used both within and between each program. Within the Hospital and Community Health Services program, for example, the measurement of need is done separately for five sectors: acute care, maternity services, mental health services, human immunodeficiency virus and acquired immunodeficiency syndrome (HIV/AIDS) treatment, and HIV prevention. For prescribing budgets, a MFF is not required because of nationwide prescribing costs. Utilization models account for 90% of each needs index, with the remaining 10% accounted for by an avoidable health inequalities factor.
Changes In The NHS Resource Allocation Formulae Over Time
There have been significant changes to the England NHS resource allocation formulae since the NHS inception in 1948.
Geographic Population Groups (The Population Index)
The population index provides the basis of the capitation formulae. Population size was introduced into the formulae from 1971, and methods used to obtain these weights have become increasingly more accurate.
First, the differing administrative boundaries for the allocation of budgets have become more refined, from the original allocations across 14 Regional Health Authorities in 1971–95, to: 100 Health Authorities in 1996–02, 303 PCTs in 2003–08, and now 152 PCTs. A higher level of disaggregation increases the accuracy in identifying need by providing greater variations across population groups.
Second, the methods used to obtain population data have also become more advanced. From 1999 population size has been derived from ‘constrained’ population data. This calculates the number of people registered with General Practitioner (GP) surgeries and unregistered patients living in the area. Constrained population data direct budgets to the population the area serves, reducing the inefficiency of directing budgets on the basis of residence (which had been the main population measure), which may under or over-estimate the populations served in the area.
From 2006 population projections from the Office of National Statistics (ONS) have been used, which given allocations are based in advance, are thought to better reflect the population served by an area. Population projections incorporate trends in birth, death, and migration.
The changes in the population index would have meant a more accurate measurement of PCT populations. It is important to ensure accurate population modeling since any inaccuracy can divert allocations away from need.
Need Measurement (Age And Additional Needs Indices)
There have been a number of reviews of the resource allocation formulae, where each has mainly been because of developments in the needs weights. Below the major developments are picked out.
The UK NHS was introduced in 1948, and at the time there was no defined procedure in place to allocate healthcare budgets across the country. The NHS was faced with funding the hospitals, beds, and staff that it had taken over. The initial method for resource allocation was to sustain funding of these services, irrespective of the differing need for healthcare services across populations of England. Funding continued in this way until 1971.
By 1971, a new funding formula, ‘The Crossman Formula’, was implemented. The formula contained three elements: population size weighted by average bed days by age and gender; bed days weighted by a national cost per bed per year; and cases (inpatient, outpatient and day cases) weighted by the national average cost per year. The inclusion of a proxy measure of need such as bed days meant that resources were being directed toward areas where they were most needed. The inclusion of bed and case volumes, however, still maintained a proportion of the budget that was allocated based on current/ inherited supply.
Criticism of the lack of a needs-driven approach resulted in the introduction of the Resource Allocation Working Party (RAWP) formula in 1976. RAWP was set up to attain a resource allocation formula that objectively, equitably and efficiently responded to relative differences in need. The RAWP formula was a weighted capitation approach to allocating resources across the country. The formula now derived capitation payments weighted by need. Need was measured by age and gender, and noting how age and gender alone would be insufficient to approximate need, ‘additional need’ was calculated using Standardized Mortality Ratios (SMRs). For the first time, the resource allocation formulae now contained non-utilization measures for need.
The RAWP formula was in place until the 1988 review of the formula was implemented in 1990. For the first time, empirical estimations on the variations of need factors on health care utilization were modeled using regression analysis of hospital utilization. Regression analysis was creating a shift from value judgments on the weighting of needs and permitted the weights on the needs variables to be adjusted for supply factors.
With the release of 1991 Census data, a further review was made in 1994 which was carried out at the University of York (Carr-Hill et al., 1994). To remove the potential endogeneity of supply, significant supply variables were removed from the regression and the regression was then reestimated.
In 1995, a Resource Allocation Group (RAG) was set up to assess resource allocation in primary care. RAG was replaced in 1997 by the Advisory Committee on Resource Allocation (ACRA), an independent expert body to ensure resources for primary and secondary care fully reflect local population needs. The Technical Advisory Group (TAG) was also set up to provide technical support.
In 2002, a further review was conducted. The new formula incorporated more updateable deprivation measures (the Indices of Deprivation), and, for the first time, a measure of unmet need. Unmet need was modeled by maintaining the coefficients with incorrect signs in the models for the descriptive regression analysis but not using these variables as prescriptive weights in the weighted capitation formulae. Supply-side variables were now maintained in the regression but like those measuring unmet need, were not used to obtain weights for need.
There are four key factors in the measuring of need: observing legitimate met and unmet need, controlling for illegitimate need by the modeling of supply-side factors on utilization, and the inclusion of a health inequalities adjustment. Econometric techniques and updates in data availability have improved the accuracy of measuring met need, and the removal of illegitimate supply-side measures of need have arguably lead to greater efficiency in the allocation of budgets.
Unmet need was not modeled until 2002, and is intrinsically difficult to capture, particularly since most resource allocation formulae use utilization data to model need. Even if unmet need is accurately modeled, this may still be inefficient unless procedures are put in place to target the removal of under-utilization of these groups. With no stipulation of how providers should spend their allocated budgets, unmet need ‘premiums’ could implicitly generate technical inefficiency if these premiums are spent on services that would be relatively less productive in health.
Differing Costs In The Delivery Of Health Care (The MFF Index)
The RAWP formula was amended in 1980–81 to weight capitations on the basis of unavoidable differences in the costs of delivering health care across the country. The MFF was applied to account for differences in staff costs. The introduction of this factor removed the inefficiency of under/over funding because of the differences in the cost of health care by region. The MFF has been updated and expanded regularly. In 2002, the number of pay zones (used to calculate the MFF index) increased from 78 to 117 and a smoothing technique was applied to reduce sharp drops in wage rates for neighboring areas. In 2006, there were further increases in pay zones to 303. In 2008 ,more up to date data were used, doctors and dentists were given their own weighting, and further smoothing techniques were implemented. Another review in 2011 updated the MFF with more recent data.
The MFF aims to correct for differences in the cost of delivering services across PCTs. Assuming high cost PCTs serve relatively more productive (in health) populations, the MFF moves budgets to a more efficient allocation, through aiming to be more equitable by adjusting for unavoidable differences in the cost of delivering health care between PCTs. This diverts budgets away from less productive populations, which again, could raise concerns over equity.
Payer’s Equity Concerns
The Department of Health and Social Security (1976) review of the resource allocation formulae set the objective ‘‘to secure, through resource allocation, that there would eventually be equal opportunity of access to health care for people at equal risk.’’ This objective is consistent with the pure efficiency solution where equal risk translates to equal marginal benefit from additional expenditure.
In 1998, ministers announced a new objective of the formulae: that of ‘‘contributing to the reduction in avoidable health inequalities’’ (Department of Health, 2011). This was incorporated into the 2002 review of the formula by the introduction of a health inequalities adjustment (based on years of life lost, measured as deviations from the average mortality rate in England). In 2008, ACRA introduced a new health inequalities adjustment, Disability Free Life Expectancy (DFLE). The DFLE combines mortality and morbidity (measured by limiting long-standing illness) data to generate expected years from birth that are free from disability or limiting long-term illness, and is compared to a baseline of 70 years.
The formulae have moved from the pure efficiency solution toward a more equitable solution (from W* to AE* in Figure 7). The health inequalities adjustment is currently given a weight of 10% in the needs indices, but this has no statistical basis.
Overall Impacts Of The Formulae Changes On Efficiency
The improvements in modeling geographic population groups, need and the incorporation of the MFF are likely to have reduced inefficiency in budget allocations enabling a better possibility of maximizing health (the pure efficient solution: W* in Figure 7). The inclusion of an avoidable health inequalities measure from 2002, however, means it is unlikely the pure efficient solution is met. Rather, the best the payer can hope to achieve would be somewhere between W* and AE* in Figure 7, resulting in relatively lower level of health (the point between W* and AE* will depend on how much weight is applied to the health inequalities adjustment). In addition, the inclusion of past allocations and the pace of change policy to formulate actual allocations make any movement toward the desired outcome slower. Including past allocations also creates issues about technical efficiency, in particular, budget risk. Under spending providers have an incentive to inflate their spending and such activities could become self-perpetuating.
Conclusion
The most efficient resource allocation funding formula requires the relative needs of the populations the payer serves to be identified. Identifying needs accurately enables the weighted capitation approach (commonly used in developed countries to allocate health care budgets) to direct budgets to those areas most efficient in producing health. This approach is consistent with higher budgets allocated to less productive populations on the basis of need, but recognizes that the maximization of health output may lead to inequalities in output between each population group.
There are a variety of reasons why the funding formulae may not be efficient. The reliance on accurately measured needs is a key concern, requiring the ability to disentangle supply-side factors, and understand and recognize the impacts of unmet need. Another key issue surrounds the adjustments that may be included for health inequalities. Equity and efficiency aims do not necessarily have to be in conflict – but they often are. Perhaps the most striking and complex impact on efficiency lies in the activity of the providers of health care. Technical inefficiency may be caused by a number of factors, and each detracts from the resource allocation funding formulae being efficient.
References:
- Carr-Hill, R. A., Hardman, G., Martin, S., et al. (1994). A formula for distributing NHS revenues based on small area use of hospital beds. York: Centre for Health Economics, University of York.
- Department of Health. (2011). Resource allocation: Weighted capitation formula. 7th ed. Available at: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/152060/dh_124947.pdf.pdf (accessed 24.06.13). Department of Health and Social Security. (1976). Sharing resources for health in
- Report of the Resource Allocation Working Party. London: Her Majesty’s Stationery Office. Available at: http://webarchive. nationalarchives.gov.uk/20130107105354/http://www.dh.gov.uk/en/ Publicationsandstatistics/Publications/PublicationsPolicyAndGuidance/DH_4121873 (accessed on 24.06.13).
- Hollingsworth, B. (2008). The measurement of efficiency and productivity of health care delivery. Health Economics 17, 1107–1128.
- Hollingsworth, B., Dawson, P. and Maniadakis, N. (1999). Efficiency measurement of health care: A review of non-parametric methods and applications. Health Care Management Science 2(3), 161–172.
- Smith, P. C. (2007). Formula funding of public services. London and New York: Routledge Taylor & Francis Group.
- Culyer, A. J. and Wagstaff, A. (1993). Equity and equality in health and health care. Journal of Health Economics 12, 431–457.
- Hauck, K., Shaw, R. and Smith, P. C. (2002). Reducing avoidable inequalities in health: A new criterion for setting health care capitation payments. Health Economics 11, 667–677.
- Jacobs, R., Smith, P. C. and Street, A. (2006). Measuring efficiency in health care. Cambridge, UK: Cambridge University Press.